前言
本文仅限昆明理工大学开设的数字信号处理及DSP应用的MATLAB结果分享。文章部分内容可能有错误,仅代表个人观点。
本文承接上一个帖子,探讨后两个实验研究的问题和解决过程。
实验四 应用DFT实现信号频谱分析
4.1 实验目的
1.进一步加深DFT算法原理和基本性质的理解。
2. 学习用FFT对连续信号和时域离散信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便在实际中正确应用FFT。
4.2 实验内容
1.考虑长度为5的有限序列,假设采样周期为0.5s。x(0)=1,x(1)=3,x(2)=5,x(3)=1,x(4)=1。要求用FFT来计算其频谱。
这题要我们利用快速傅里叶变换FFT求数字信号的频谱。简单一点的思维是直接将数字信号保存至数组,然后直接FFT求结果,甚至不需要用到采样周期。
但是这里需要考虑数字信号的部分特征:序列长度和采样频率。且由于信号的频谱共轭对称性,我们可以将FFT的结果对称于零频率,方便计算与理解。
%% 任务一
x1 = [1, 3, 5, 1, 1];
T = 0.5; %给定原始数据
D = 2 .* pi / (5 .* T); %求出序列长度及频率分辨率
k = floor(-2 : 2); %求对称于零频率的FFT位置向量
Y1 = fftshift(fft(x1)); %求对称于零频率的FFT序列值
figure
subplot(2,1,1)
plot(k .* D, abs(Y1), 'o-') %画幅频特性图
title('幅频特性图');
subplot(2,1,2)
plot(k .* D, angle(Y1), 'o-') %画相频特性图
title('相频特性图');由此可以得到输出图像。

这一图像与目标结果存在差距,个人认为是序列x导致的。将序列x换成[1, 3, 5, 3, 1],就能够得到预期结果。

2. 用fft函数对 进行频谱分析,其中
进行频谱分析,其中 ,
, 。以采样频率
。以采样频率 对其进行采样,要求:(1)截取信号长度为32点,并作出2048点DFT,画出幅频曲线;(2) 截取信号长度为512点,并作出2048点DFT,画出幅频曲线。
对其进行采样,要求:(1)截取信号长度为32点,并作出2048点DFT,画出幅频曲线;(2) 截取信号长度为512点,并作出2048点DFT,画出幅频曲线。
这里需要注意从函数中截取32或512点,并作2048点的离散傅里叶变换DFT。明显截取的点数比需要变换的点数少,在DSP中这种情况多半可以使用0在末尾补齐。这样不会改变原始信号的信息。
%% 任务二
f1 = 20000; f2 = 21000; fs = 80000;
f = @(x) cos(2 .* pi .* f1 .* x) + 2 .* cos(2 .* pi .* f2 .* x); %设置函数xa
n1 = 32;
t1 = (0:n1 - 1) / fs;
x1 = f(t1); %截取信号长度32点
n2 = 512;
t2 = (0:n2 - 1) / fs;
x2 = f(t2); %截取信号长度512点
nf = 2048;
xadd1 = [x1, zeros(1, nf - n1)];
xadd2 = [x2, zeros(1, nf - n2)]; % 零填充到2048点
f = (0:nf - 1) * (fs / nf);
y1 = fft(xadd1);
fx1 = abs(y1) / nf;
y2 = fft(xadd2);
fx2 = abs(y2) / nf; %取幅频谱
#figure
#subplot(2,1,1)
#plot(t1, x1);
#title('取样32点时域波形');
#subplot(2,1,2)
#plot(f, fx1);
#title('取样32点幅频特性');
figure
subplot(2,1,1)
plot(t2, x2);
title('取样512点时域波形');
subplot(2,1,2)
plot(f, fx2);
title('取样512点幅频特性');由于预期结果中并没有取32点的DFT幅频曲线,因此在这里我把它注释了。

4.3 实验步骤
1. 复习DFT的定义、性质和用DFT做谱分析的有关内容。
2. 复习FFT算法原理与编程思想,并对照DFT-FFT运算流图和程序框图,读懂FFT程序。
这两部分就不复习了,理论会了实验就易如反掌。
3. 实验内容1的程序运行结果如下图所示:
4. 实验内容2的程序运行结果如下图所示:
这两部分就不展示了,与本人画出的结果大同小异。
4.4 实验思考题
1.思考在做DFT时,补零会提高分辨率吗?
补零是在信号末尾添加零值,不会引入新的信息或改变原始信号的实际内容,但会增加DFT的点数,从而提高频率分辨率。因此,补零后的信号在时域上看起来像是原始信号后面跟着一段零值,但在频域上,它提供了更高的频率分辨率。
2. 做DFT时信号点数的不同对信号的幅频特性有何影响?
当DFT的点数增加时,频率分辨率随之提高。这意味着能够更精确地分辨出接近的频率分量。相反,如果DFT的点数较少,频率分辨率将降低,可能导致无法准确区分接近的频率分量。
实验五 IIR数字滤波器设计
5.1 实验目的
1. 熟悉用冲激响应不变法、双线性变换法设计IIR数字滤波器的原理与方法。
2. 掌握数字Butterworth滤波器的设计方法。
5.2 实验内容
1.用MATLAB设计Butterworth数字低通滤波器,设计指标如下:通带为 ,阻带为
,阻带为 ,
, ,
, ,采样频率为4000Hz,分别用冲激响应不变法和双线性变换法求系统函数H(z),并分别画出幅频响应和相频响应曲线。
,采样频率为4000Hz,分别用冲激响应不变法和双线性变换法求系统函数H(z),并分别画出幅频响应和相频响应曲线。
巴特沃斯IIR数字滤波器,通带小于400Hz、最大通带衰减2dB,阻带大于600Hz、最小阻带衰减40dB。利用MATLAB自带的buttord函数可以计算数字低通滤波器的阶数和截止频率,再利用butter函数计算传递函数表达式,分别利用impinvar和bilinear计算冲激响应不变法和双线性变换法建立数字滤波器、freq函数获得复频域响应。
clear all
%% 前置条件
fn = 4000; fp = 400; fs = 600;
ap = 2; as = 40;
%% 冲激响应不变法
wp1 = 2 .* pi .* fp;
wr1 = 2 .* pi .* fs;
[N1, wn1] = buttord(wp1, wr1, ap, as, 's');
[B1, A1] = butter(N1, wn1, 's');
[num1, den1] = impinvar(B1, A1, fn);
[h1, w] = freqz(num1, den1);
abs1 = 20 .* log10(abs(h1));
angle1 = angle(h1);
%% 双线性变换法
wp2 = 2 .* pi .* fp;
wr2 = 2 .* pi .* fs;
[N2, wn2] = buttord(wp2, wr2, ap, as, 's');
[B2, A2] = butter(N2, wn2, 's');
[num2, den2] = bilinear(B2, A2, fn);
[h2, w] = freqz(num2, den2);
abs2 = 20 .* log10(abs(h2));
angle2 = angle(h2);
%% 图像
f = w ./ (2 .* pi) .* fn;
figure %幅频特性
hold on
plot(f, abs1, '-.')%画脉冲响应不变法
plot(f, abs2, '-') %画双线性变换法
axis([0 2000 -50 10])
xticklabels(0:0.1:1)
grid on
xlabel('频率');
ylabel('幅度');
title('巴特沃思数字低通滤波器');
legend('脉冲响应不变法', '双线性变换法'); %图像注记
hold off
figure %相频特性
hold on
plot(f, angle1, '-.')
plot(f, angle2, '-')
axis([0 2000 -50 10])
xticklabels(0:0.1:1)
grid on
xlabel('频率');
ylabel('相位');
hold off
幅度谱和预期结果差距较小,但是相位谱就差距较大,问题的缘由目前还没查明,可能是函数用错或是理解错了,也欢迎指正。


5.3 实验步骤
1. 复习有关Butterworth模拟滤波器设计和用冲激响应不变法和双线性变换法设计IIR数字滤波器的内容,用双线性变换法设计数字滤波器系统函数。
这部分就暂时不复习了。
2. 实验内容1的程序运行结果如下图所示:
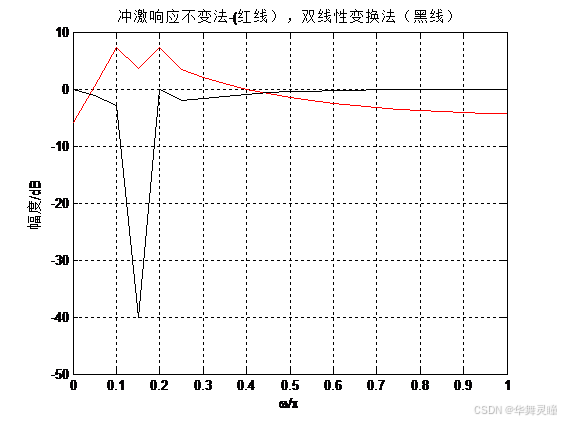
3. 实验内容2的程序运行结果如下图所示:(实验任务书编号有误,这里修改)
由于相频谱的图像与预期不同,这里附上预期结果
5.4 实验思考题
1.用双线性变换法设计数字滤波器过程中,变换公式 中T的取值对设计结果有无影响?为什么?
中T的取值对设计结果有无影响?为什么?
双线性变换法是一种将模拟滤波器转换为数字滤波器的方法,将模拟滤波器的频率响应通过某种映射关系转换到数字滤波器的频率响应上。这个映射关系与采样周期T密切相关。采样周期T的选择决定了模拟频率和数字频率之间的转换关系。
如果T取值较大,意味着采样频率较低,这会导致数字滤波器的频率响应在高频部分因奈氏采样定理出现失真或混叠现象,导致失真。如果T取值较小,即采样频率较高,那么数字滤波器就能够更准确地表示模拟滤波器的频率响应。但是,过高的采样频率也会增加数字滤波器的计算复杂度和资源消耗。
2.为什么冲激响应不变法会产生频率混叠的问题?
冲激响应不变法是基于时域抽样定理,它要求数字滤波器的冲激响应对应于模拟滤波器传递函数的等间隔抽样。在频率域上,这种抽样会导致模拟滤波器的频谱被周期延拓,低采样频率会产生混叠现象。
结论
感谢
Sol-itude的文章数字信号处理用脉冲响应不变法和双线性变换法设计巴特沃斯滤波器MATLAB实现——实例_双线性变换例题-CSDN博客给我的启发
全文全部是本人一个人完成,存在错误,允许指正,不允许因为本人专业程度低而出现对本人的诋毁、骂人等现象。
技术是开拓、完善、传承的过程。开拓的过程是艰苦,完善的过程是漫长的,传承的过程是延续的。愿技术能在传承的基础上开拓,能在开拓的道路上完善,能在完善的成果中继承,生生不息,永无止尽!
全部实验内容已放至百度云盘百度网盘,提取码slwk。























 266
266

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








