MATLAB卷积函数conv的运算原理对信号幅值的影响

卷积是理工科学习中一种十分重要的运算，我个人在使用MATLAB中的卷积函数conv时遇到了一点点的“异常”，即卷积后信号（函数）的幅值与理论值不符。在查阅相关资料了解到了conv函数的实际运算原理后，在一定程度上解决了我的困惑，在这里我将对这一现象进行呈现，分析与解决，欢迎大家进行指导。
 

问题背景

在学习信号与系统课程时，我想使用MATLAB验证一下矩形信号卷积的图像变化特性，但是得到的图样与实际情况不符，出现了“放大现象”。

代码

t = -20:0.01:20;
f_1 = heaviside(t-1)-heaviside(t-3);
f_2 = heaviside(t+3)-heaviside(t+1);
f_3 = conv(f_1, f_2, 'same');
plot(t, f_3);

运行结果

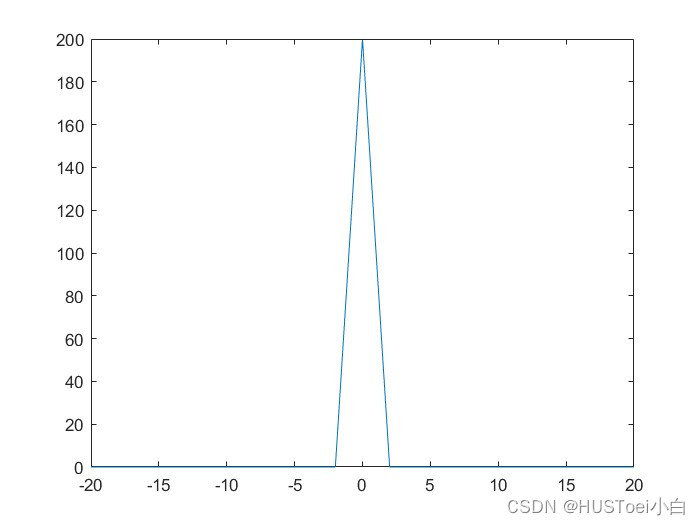
与理论运算结果相比不难发现，图样的峰值与理论值2不符，而且整整放大了100倍。

问题解决

经过资料的查找，可以知道MATLAB中的conv函数实际上执行的是多项式的乘法，即两个向量之间在倒置移位后的点乘运算，并不是连续信号卷积时应该进行的积分操作，这就导致了信号会出现等比例放大的情况。至于放大倍数，与我们选取的自变量间隔直接相关，上述代码的自变量间隔为0.01，即单位长度上对应了100个采样点，最后卷积结果的幅值也就自然变为理论值的100倍。如果我们对代码进行小小的修改，即对卷积结果的函数点乘0.01：

代码

t = -20:0.01:20;
f_1 = heaviside(t-1)-heaviside(t-3);
f_2 = heaviside(t+3)-heaviside(t+1);
f_3 = 0.01.*conv(f_1, f_2, 'same');
plot(t, f_3);

运行结果

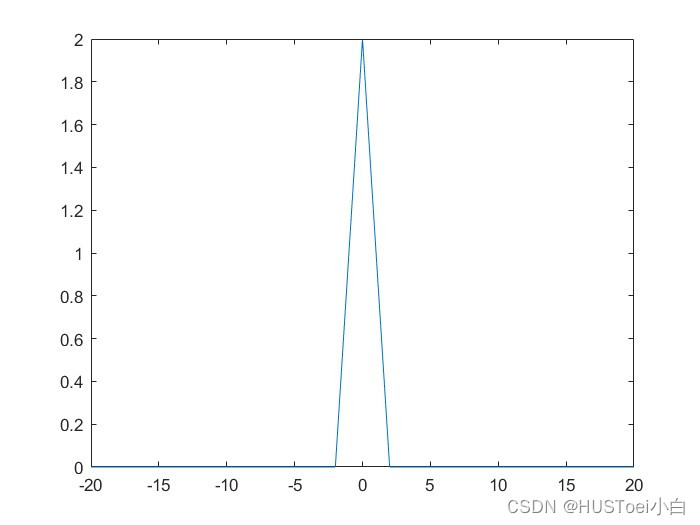
结论验证

我们取更细的自变量间隔，代码变为：

代码

t = -20:0.001:20;
f_1 = heaviside(t-1)-heaviside(t-3);
f_2 = heaviside(t+3)-heaviside(t+1);
f_3 = conv(f_1, f_2, 'same');
plot(t, f_3);

理论上图样的幅值会放大1000倍，运行代码进行验证：

运行结果

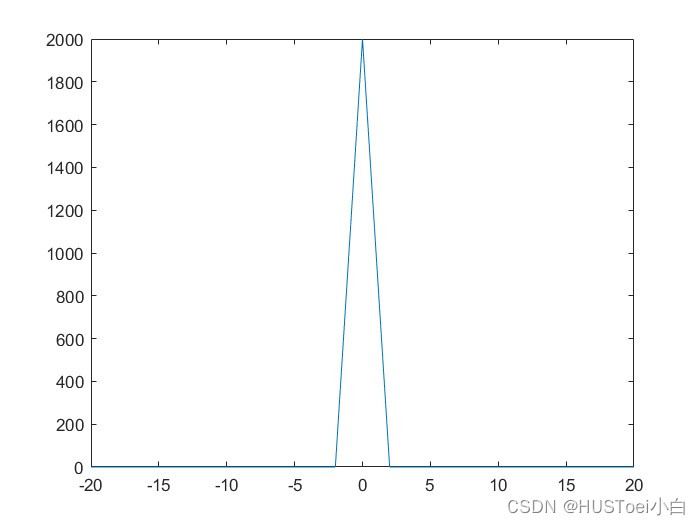
与我们的预测相符，即验证。

讨论

可能会有人提出近一步减小自变量间隔至1，以期得到不失真的图样，但实际不然，在MATLAB中我们是通过取大量的离散点来模拟连续函数，自变量的间隔与连续性的好坏息息相关，所以我认为对于这种幅值放大的现象，还是不改变取样间隔，而是后续对卷积结果的函数点乘一个间隔的倒数为宜。