仅用与非门实现一位数值的比较电路

在数字电路的组合逻辑设计中，为了实现资源的优化，我们总是希望使用尽可能最少的逻辑门函数种类，又考虑到任意的逻辑函数都可以化简为一定数量的“与-或”式组合，自然，我们便可以仅用与非门来实现任意的组合逻辑电路。

题目描述

在电测实验中一次的设计就考察了上面思想的运用，题目是设计一个一位数值的比较电路，并且通过LED的点亮来输出结果。考虑到我们的实验中并没有提供或非门芯片，多次灵活使用与非门芯片就成了设计的关键。

题目分析

考虑两路输入分别为A，B。那么最后结果无非为三种，即A>B，A<B和A=B。通过“与-或”式进行组合也就是，和。在知道逻辑函数的对应表达式后，主要的问题就是将其转化为“与-或”式的组合。其中最常见的使用方式是：

取反：

或运算：

基础设计

在此基础上，我们就可以得到最直接的设计思路，三种比较情况的逻辑函数转化为：

A>B：（取反）

A<B：（取反）

A=B：（原式）

考虑到第三式没有取反，在电路设计的时候我们需要再加上一个取反单路，然后对于LED灯使用共阳极连接，低电平有效的点亮方式。

在硬件仿真平台Proteus上进行仿真，结果如下（此时A为高电平，B为低电平。红点代表高电平，蓝点代表低电平）：

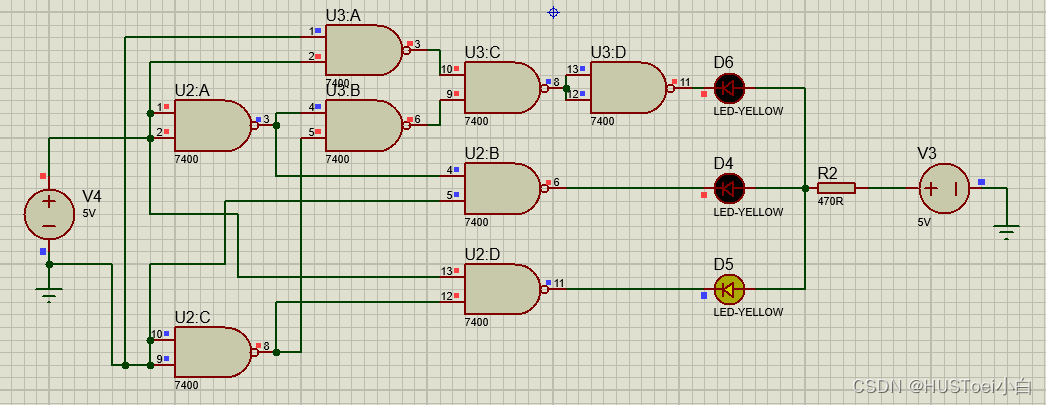
简化设计

以上的电路设计很直观，步步为营，但是很有可能不是最简的设计，特别是采用与非门来构成大量的非门，很容易造成与非门的资源浪费，下面介绍一种更加简单的设计，仅仅使用了4个与非门（一块74HC00即可）：

A>B：（取反）

A<B：（取反）

A=B：（取反）

但这样的设计肯定对于逻辑函数的等价变化技巧有较高的要求，笔者也算是有试出来的成分。在硬件仿真平台Proteus上进行仿真，结果如下（此时A为高电平，B为低电平。红点代表高电平，蓝点代表低电平）：

在Cadence17.4中画出电路图并直流仿真，结果如下（里面不少LED无法参与仿真，迫于无奈我选了个不了解的MLED，感觉影响应该不大）：

可见这样的电路设计是可行的。