HDU电磁场与微波实验三——分布参数低通滤波器的设计、仿真和分析

一、实验内容

采用微带传输线设计低通滤波器；

设计指标：截止频率：500MHz

                  通带内（500MHz以下）：S21>-0.5dB,S11<-20dB

                  阻带内：900MHz以上，S21<-30dB

仿真频段100MHz-1000MHz，步长10MHz，要求电路对称，端口阻抗50欧姆。

二、实验步骤

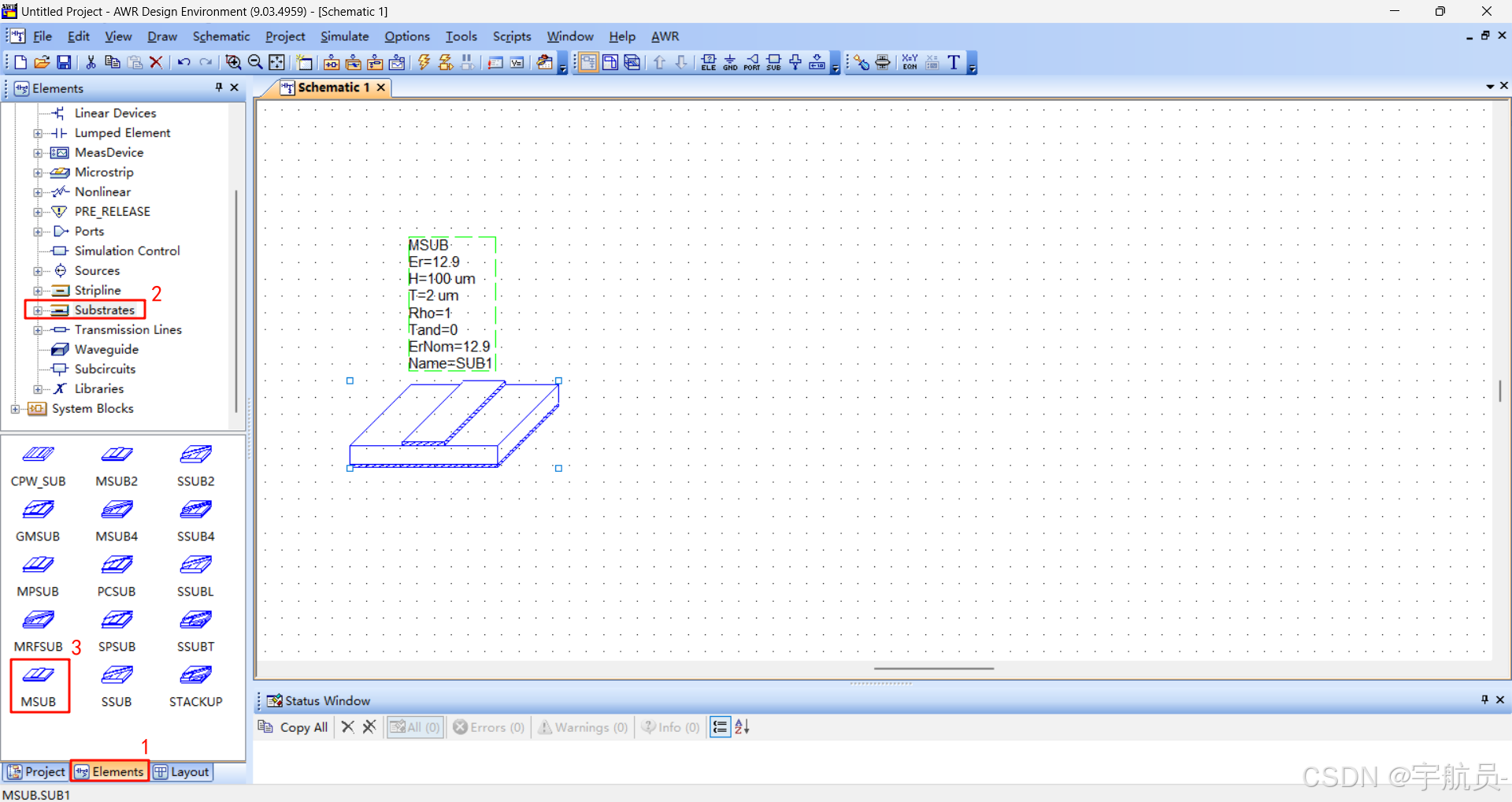
设置基本参数

创建原理图，右键Circuit Schematics

设置微带线参数，双击MSUB

画原理图

编辑参数，双击各元件

创建结果图

右键Graphs生成结果图，右键结果图，选择Add Measurement

计算参数

上方工具栏选择tools->TXline，根据参数计算出L值

由结果可知，d1=d3=86.2233，d2=d4=78.3409，创建变量。

在上方工具栏找到Analyze，生成结果图。

接下来对结果图进行优化。

找到Project->Optimizer Goals，右键选择Add Optimizer Goal，添加三个优化条件。

工具栏选择simulate->Optimize

返回Optimizer界面点击start开始优化，Cost为0优化完成，d1-d4自动修改。

再次Analyze，生成优化后的最终结果图。

生成版图

希望每一位HDUer都能笑着上完实验课，respect