层次分析法（AHP）(案例+Python实现)

s_Iris_

已于 2024-07-15 18:52:51 修改

阅读量483

点赞数 10

文章标签： python 开发语言

于 2024-07-15 18:50:50 首次发布

本文链接：https://blog.csdn.net/2301_77056280/article/details/140414196

版权

[参考内容]：层次分析法（AHP）步骤详解_哔哩哔哩_bilibili

这位老师讲得很好，我将视频内容做了下总结，并用代码实现了一下

一、问题

小明想出游，备选目的地有三个：南京，桂林和三亚，考虑因素有四个：景观、吃住、人文和价格。现需要更具各个要素科学的选出小明最终该去的目的地。

二、构建层次结构

三、构建判断矩阵

指标之间比较量化值规定

因素 i 比因素 j	量化值
同等重要	1
稍微重要	3
较强重要	5
强烈重要	7
极端重要	9
两相邻判断的中间值	2、4、6、8
倒数	$a_{i.j}=\frac{1}{aji}$

目标层和指标层判断矩阵

Z	A1景色	A2吃住	A3价格	A4人文
A1景色	1	1/4	2	1/3
A2吃住	4	1	8	2
A3价格	1/2	1/8	1	1/5
A4人文	3	1/2	5	1
sum	8.50	1.88	16.00	3.53

判断矩阵的主对角线值为 1 ，因为自己和自己同等重要。最后一行 sum 是每一列的求和，为后续归一化作准备。

四、计算各层要素对应权重（算术平均法求权重）

按列归一化

$a_{i,j}=\sum_{i = 1}^{n}a_{i,j}$

归一化后矩阵：

Z	A1景色	A2吃住	A3价格	A4人文
A1景色	0.12	0.13	0.13	0.1176
A2吃住	0.47	0.53	0.50	0.57
A3价格	0.06	0.07	0.06	0.06
A3价格	0.35	0.27	0.31	0.28

计算 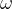$\omega$

这里我们可以近似认为 $\omega$ 为矩阵Z的特征向量，并且将特征向量作为指标的权重值。

$\omega_{i} = \frac{\sum_{j=1}^{n}a_{i,j}}{n}$

更新矩阵

Z	A1景色	A2吃住	A3价格	A4人文	$\omega$
A1景色	0.12	0.13	0.13	0.1176	0.1176
A2吃住	0.47	0.53	0.50	0.57	0.5175
A3价格	0.06	0.07	0.06	0.06	0.0611
A3价格	0.35	0.27	0.31	0.28	0.3038

五、一致性检验

一致性检验保证了逻辑不会出现混乱，即出现 A比B好，B比C好，C比A好这样的情况出现。

求矩阵特征值

这里我们采用近似算法

$\lambda_{max}=\sum_{i=1}{n}\frac{[AW]_{i}}{n\omega_{i}}$

式中，n 为矩阵的阶数，AW中的A为归一化后的矩阵，W为 $\omega$ 特征向量，计算方式为矩阵乘法。

$\omega$	AW
0.1176	0.47
0.5175	2.08
0.0611	0.25
0.3038	1.22

计算特征值 $\lambda_{max}$ ：

$\lambda_{max}=\frac{1}{4}\times (\frac{0.47}{0.1176}+\frac{2.08}{0.5175}+\frac{0.25}{0.0611}+\frac{1.22}{0.3038})=4.0155$

计算CI

$CI = \frac{\lambda-n}{n-1}=0.0052$

计算RI

RI 值查表即可

RI 值
阶数n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
RI值	0.00	0.00	0.52	0.89	1.12	1.26	1.36	1.41	1.46	1.49	1.52	1.54	1.56	1.58	1.59

这里我们是4阶矩阵，所以取 RI 值为 0/89

计算CR

$CR=\frac{CI}{RI}=0.0058$

如果 CR 值小于 0.1 ，则认为通过一致性检验，否则未通过一致性检验，需要检查矩阵逻辑是否正确，如果矩阵任意两行之间成比例，则一致性检验结果 CR = 0

六、方案层计算

方案层的计算同指标层相同，重复三、四、五步骤即可。

此时我们分别考虑每个地点的指标如何，构建如下矩阵，并计算特征向量。

A1景色

A1景色	南京	桂林	三亚	$\omega$
南京	1	1/4	2	0.1818
桂林	4	1	8	0.7273
三亚	1/2	1/8	1	0.2727

A2吃住

A2吃住	南京	桂林	三亚	$\omega$
南京	1	5	2	0.5714
桂林	1/5	1	1/2	0.1429
三亚	1/2	2	1	0.2857

A3价格

A3价格	南京	桂林	三亚	$\omega$
南京	1	1/3	2	0.2299
桂林	3	1	5	0.6479
三亚	1/2	1/5	1	0.1222

A4人文

A4人文	南京	桂林	三亚	$\omega$
南京	1	5	7	0.7380
桂林	1/5	1	2	0.1676
三亚	1/7	1/2	1	0.0944

七、决策

最后我们构建总的决策矩阵

Z	四个指标的权重	南京	桂林	三亚
A1景色	0.1171	0.1818	0.7273	0.2727
A2吃住	0.5183	0.5714	0.1429	0.2857
A3价格	0.0613	0.2299	0.6479	0.1222
A4人文	0.3033	0.7380	0.1676	0.0944

最后计算加权平均值，计算方法即为每个城市在该指标下的得分乘以该指标的权重，例如南京得分：

$0.1171\times0.1818+0.5183\times0.5714+0.0613\times0.2299+0.3033\times0.7380=0.56746$

城市	南京	桂林	三亚
得分	0.56746	0.24254	0.189991

最后南京得分最高，我们应该选择南京。

八、代码实现

使用python实现

其中.xlxs文件即使为判断矩阵

sheet1:

sheet2:

sheet3:

sheet4:

sheet5:

"""
@ s_Iris_
AHP
"""

import pandas as pd
import numpy as np

# RI表
RI_sheet = {'1': 0, '2': 0, '3': 0.52, '4': 0.89, '5': 1.12, '6': 1.26, '7': 1.36,
      '8': 1.41, '9': 1.46, '10': 1.49, '11': 1.52, '12': 1.54, '13': 1.56,
      '14': 1.58, '15': 1.59}

# 导入数据
Z1 = pd.read_excel('./evaluate.xlsx', sheet_name='Sheet1')
A1 = pd.read_excel('./evaluate.xlsx', sheet_name='Sheet2')
A2 = pd.read_excel('./evaluate.xlsx', sheet_name='Sheet3')
A3 = pd.read_excel('./evaluate.xlsx', sheet_name='Sheet4')
A4 = pd.read_excel('./evaluate.xlsx', sheet_name='Sheet5')
evaluate_list = np.array(Z1.iloc[:, 0])

#将数据转换为numpy
Z1_arr = np.array(Z1.iloc[:, 1:5])
A1_arr = np.array(A1.iloc[:, 1:5])
A2_arr = np.array(A2.iloc[:, 1:5])
A3_arr = np.array(A3.iloc[:, 1:5])
A4_arr = np.array(A4.iloc[:, 1:5])
lo_name = np.array(A1.iloc[:, 0])

def uniformization(arr):
    """
    :param arr: 需要按列归一化的矩阵
    :return: 按列归一化的矩阵, 归一化后矩阵的近似特征值
    """
    nui_arr = np.zeros_like(arr)
    nui_arr[:] = arr[:]
    shape = nui_arr.shape
    sum = nui_arr.sum(axis=0)
    for n in range(0, shape[1]):
        nui_arr[:, n] = nui_arr[:, n] / sum[n]

    omega = nui_arr.sum(axis=1) / shape[1]
    return nui_arr, omega

def consistency(arr, omega):
    """
    :param arr: 需要检验的数组
    :param omega: 特征向量
    :return: CI: RI, CR，flag为1则通过一致性检验，为0则未通过
    """
    flag = 0
    __arr__ = np.zeros_like(arr)
    __arr__[:] = arr[:]
    shape = __arr__.shape
    n = shape[1]
    a_omega = __arr__ @ omega
    Lambda = np.sum((a_omega / omega) / n)
    CI = (Lambda - n) / (n - 1)
    RI = RI_sheet[str(n)]
    CR = CI / RI
    if CR <= 0.1:
        print("通过一致性检验")
        flag = 1
    else:
        print("未通过一致性检验")
        flag = 0

    return (CI, RI, CR, flag)

def main():
    data = []
    data.append(Z1_arr)
    data.append(A1_arr)
    data.append(A2_arr)
    data.append(A3_arr)
    data.append(A4_arr)

    data_characteristic = []
    uni_data = []
    data_omega = []

    for i in range(0, len(data)):
        uni_arr, omega = uniformization(data[i])
        uni_data.append(uni_arr)
        data_omega.append(omega)
        characteristic = consistency(data[i], omega)
        if characteristic[3] == 0:
            print("一致性检验不合格！！")
            return
        data_characteristic.append(characteristic)
    print("所有数据均通过一致性检验！")

    Z = np.zeros((len(evaluate_list), (len(lo_name)+1)), dtype=float)
    Z[:, 0] = data_omega[0]
    for i in range(0, len(evaluate_list)):
        Z[i, 1:(len(lo_name)+1)] = data_omega[i+1]

    print("决策矩阵:")
    print(Z)

    shape = Z.shape
    sum = []
    weight = data_omega[0]
    for i in range(1, shape[1]):
        sum1 = np.dot(weight, Z[:, i])
        sum.append(sum1)

    print("加权平均值:")
    print(sum)

    decision = np.argmax(sum)
    decision = lo_name[decision]

    print("最终决定:")
    print(decision)

if __name__ == '__main__':
    main()

运行结果：