立个 flag 在这里,暑假学完数值分析方法(本科版),等我学完后再回这 flag 来看看。

[参考教材]:《数值计算方法》马东升 董宁
[参考视频]:数值计算方法 数值分析 计算方法_哔哩哔哩_bilibili
一、非线性方程组定义
方程 f(x)=0 当 f(x)是一次多项式时,称f(x)为线性方程。
代数多项式方程
超越方程
重根
若 ,m为正整数,则称
为
的 m 重根。若函数
有 m 阶连续导数,方程
的充要条件是:
二、方程求根特点
1、根的存在性
n次代数方程有n个根
2、根的分布
在 [a,b] 内连续,且
(即f(a)和f(b)异号),则在[a, b]内 f(x)=0 至少有一个根。(有根区间)
在 [a,b] 内连续,严格单调,且
(即f(a)和f(b)异号),则在[a, b]内 f(x)=0 有且仅有一个根。(隔根区间)
确定隔根区间的方法:
- 作 y=f(x) 的草图,看 f(x) 与 x 轴交点定 [a, b]
- 逐步搜索,在连续区间 [a, b] 内,选取适当的
, 若
,则
内有根。
- 根的精确化,将区间逐步缩小,直到找到更加精确的根。
三、二分法
1、区间对分
将区间对分,判别 f(x) 的符号,逐步缩小有根区间。
2、方法
流程图如下,其中 为预先给定的精度

重复上述流程,直到找到方程的根。
3、收敛性
由二分法产生一个有根区间:
关于 的区间长度:
当 k 足够大时,取近似值 为方程的根
误差:
先验估计,设 为给定精度要求,可确定分半次数k使得
两边取对数得到
4、例题
用二分法求 在 [1, 2] 内的根,要求绝对误差不超过
求出,f(1)=-5, f(2)=14
| k | 有根区间 | 中点 | f(x) |
| 0 | [1, 2] | 1.5 | f(1.5)=2.375>0 |
| 1 | [1, 1.5] | 1.25 | f(1.25)=-1.796875<0 |
| 2 | [1.25, 1.5] | 1.375 | f(1.375)=0.162109>0 |
| 3 | [1.25, 1.375] | 1.313 | f(1.313)=-0.840553<0 |
| 4 | [1.313, 1.375] | 1.344 | f(1.344)=-0.346940<0 |
| 5 | [1.344, 1.375] | 1.360 | f(1.360)=-0.086144<0 |
| 6 | [1.360, 1.375] | 1.368 | f(1.368)=0.045804>0 |
| 7 | [1.360, 1.368] | 1.364 | f(1.364)=-0.020299<0 |
上述表格中:
ps:要求精确到小数后第三位,即使要求
5、二分法评价
- 优点:计算简单,方法可靠,只要求f(x)连续
- 缺点:不能求重根,不能求复根,收敛速度不算太快
在求方程近似根时,一般不单独使用,常用来为其他方法提供初值
6、代码实现
挺简单的,改一下fx就好
"""
@ S_Iris
method of bisection
"""
def fx(x):
ans = x**3+4*(x**2)-10
return ans
def bisection(fx, a, b, epsilon):
if a < b:
ak = a
bk = b
elif a == b:
return a
else:
ak = b
bk = a
k = 0
xmid = ak
while (bk - ak)/2 >= epsilon:
xmid = ak + (bk - ak)/2
ans = fx(xmid)
if ans < 0:
ak = xmid
elif ans == 0:
return xmid
else:
bk = xmid
xmid = ak + (bk - ak) / 2
return xmid
def main():
a = 1
b = 2
epsilon = 0.005
x = bisection(fx, a, b, epsilon)
print("方程的近似解为{}".format(x))
if __name__ == "__main__":
main()四、迭代法
1、迭代法的一般过程
- 改写方程 f(x)=0 为 x=g(x)形式,要求g(x)连续且收敛
- 建立迭代格式:
,得到序列
- 若
收敛,必收敛到 f(x)=0 的根:
- 若
收敛,即
,则:
2、几何表示
交集即为真根

3、例题
【例】用迭代法求方程 的根
解法一:
- 方程改写为
- 建立迭代公式
- 取
(设初值),则根据迭代公式有
- 当
时,
解法二(反例):
- 方程改写成
- 建立迭代公式
- 取
(设初值),则根据迭代公式有
,当
,
,发散。
从以上两个例子可以看出,迭代法必须要求迭代函数的导数满足条件:
4、整体收敛性
考虑方程 x=g(x),若:
- 当
时,
;
使得
对
成立。则任取
,由
得到的序列
收敛于 g(x) 在 [a, b]上的唯一不动点,并且有误差估计式:
(1)
(2)
且存在极限
5、局部收敛性
如果函数 g(x) 在 的一个领域
内连续可微,
为方程 x=g(x) 的根,且
,则存在正整数
,使得对任意
,迭代序列
收敛于
6、代码实现
使用了 SymPy 库来进行收敛性判断,使用时需要注意数据格式
"""
@ S_Iris
iteration_method
"""
import sympy
def iteration(expr, x_, x0, precision_):
"""
:param expr: gx表达式
:param x_: 变量符号
:param x0: 初值
:param precision_:精度要求
:return: 是否收敛(bool),根x*
"""
a = str(x_)
precision = precision_
x = sympy.symbols(a)
gx = expr
print("gx={}".format(gx))
d_gx = sympy.diff(gx, x)
x_k = x0
while abs((gx.subs(x, x_k)).evalf()-x_k) > precision:
# 判断收敛性
if d_gx.subs(x, x_k).evalf() > 1:
print("gx不收敛!!!")
return False, 0
x_k = gx.subs(x, x_k)
x_k = x_k.evalf()
print("x*:{}".format(x_k))
return True, x_k
def main():
fx = "x**2-2*x-3"
fx = sympy.sympify(fx)
print("fx={}".format(fx))
x = sympy.symbols('x')
expr1 = sympy.sqrt(2*x+3)
expr2 = 0.5*((x**2)-3)
precision = 10**(-9)
print("gx表达式1")
flag1, ans1 = iteration(expr1, x, 4.0, precision)
print("gx表达式2")
flag2, ans2 = iteration(expr2, x, 4.0, precision)
if __name__ == "__main__":
main()运行结果:

可以看到与理论计算结果一致。
五、牛顿迭代法
1、原理
- 在迭代法中构造 g(x) 的一条重要途径:用近似方程代替原方程求根
- 牛顿法的思想是将非线性方程线性化。
2、方法(Taylor展开)
设 是
的一个近似根,将
在
出做一阶泰勒展开得到
舍掉余项得:
则有 近似为
解出
将 写成
,得到迭代公式
3、几何意义
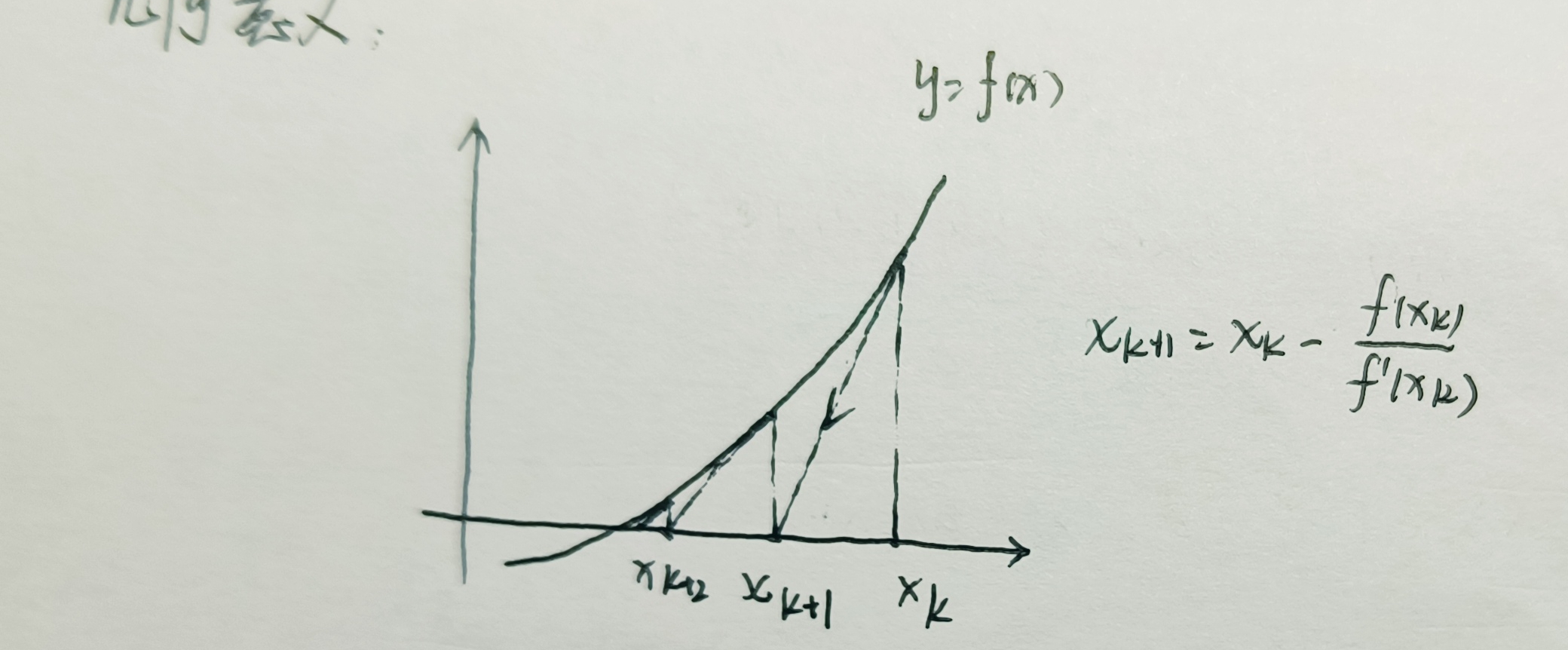
4、例题
【例】用牛顿法求 的根
解:
- 显然,
,方程于 [0, 2] 内有一根。
- 求导
- 迭代公式
()
(1)取
| k | |
| 0 | 1.0 |
| 1 | -1.15599 |
| 2 | 0.189438 |
| 3 | 0.714043 |
| 4 | 0.782542 |
| 5 | 0.783595 |
| 6 | 0.783596 |
此时迭代公式收敛
(2)取
| k | |
| 0 | 8.0 |
| 1 | 34.778107 |
| 2 | 869.1519 |
此时迭代公式发散
当初值 选取靠近根
的时候,牛顿法收敛快,当初值
不是选取接近方程根时,牛顿法可能会给出发散的结果。
5、收敛定理(牛顿法)
收敛的充分条件,设 若
; (有根)
- 在整个 [a, b] 上
不变号且
;(根唯一)
- 选取
使得
;(保证收敛)
则用牛顿法产生的序列 收敛到
在 [a, b] 的唯一根。
局部收敛:
,若
为
在 [a, b] 上的根,且
,则在
的邻域
使得任取初值
,牛顿法产生的序列
收敛到
,且满足:
6、代码实现
由于牛顿法的收敛是充分条件,不是必要条件,不方便直接判断收敛性,所以我们设置一个最大迭代次数,如果超过最大迭代次数还未得到结果,则认为该初值条件发散。
"""
@ S_Iris
newton_iteration_method
"""
import sympy
def newton_teration(expr, x_, x0, precision_, m):
"""
:param expr: gx表达式
:param x_: 变量符号
:param x0: 初值
:param precision_:精度要求
:param m: 最高迭代次数
:return: 是否收敛(bool),根x*
"""
a = str(x_)
precision = precision_
x = sympy.symbols(a)
fx = expr
d_fx = sympy.diff(fx, x)
d_2_fx = sympy.diff(d_fx, x)
x_k = x0
x_k_add_1 = fx/d_fx
n = 0
while abs((fx.subs(x, x_k)).evalf()) > precision and n < m:
n += 1
print("\r迭代{}轮:".format(n), end="")
x_k = x_k - x_k_add_1.subs(x, x_k).evalf()
# print("第{}轮x_k值为:{}".format(n, x_k))
if n == m:
print("未找到解,初值条件可能不收敛")
return False, 0
print("找到方程的根")
print("x*:{}".format(x_k))
return True, x_k
def main():
x = sympy.symbols('x')
fx = "exp(-x/4)*(2-x)-1"
fx = sympy.sympify(fx)
print("fx={}".format(fx))
precision = 10**(-9)
print("初值为0.0")
flag1, ans1 = newton_teration(fx, x, 0.0, precision, 100)
print("初值为1.0")
flag1, ans1 = newton_teration(fx, x, 1.0, precision, 100)
print("初值为2.0")
flag1, ans1 = newton_teration(fx, x, 2.0, precision, 100)
print("初值为3.0")
flag1, ans1 = newton_teration(fx, x, 3.0, precision, 100)
print("初值为5.9")
flag1, ans1 = newton_teration(fx, x, 5.9, precision, 100)
print("初值为5.95")
flag1, ans1 = newton_teration(fx, x, 5.95, precision, 100)
print("初值为5.999999999")
flag1, ans1 = newton_teration(fx, x, 5.999999999, precision, 100)
# print("初值为6.0")
# flag1, ans1 = newton_teration(fx, x, 6.0, precision, 100)
# print("初值为6.0000001")
# flag1, ans1 = newton_teration(fx, x, 6.0000001, precision, 100)
# print("初值为6.001")
# flag1, ans1 = newton_teration(fx, x, 6.001, precision, 100)
# print("初值为8.0")
# flag1, ans1 = newton_teration(fx, x, 8.0, precision, 100)
if __name__ == "__main__":
main()运行结果,这个运行结果十分有趣,我尝试了几个初值条件,最后发现 这个初值条件十分特殊。
直接看运行结果

我们可以看到在初值条件5.9及一下时,都能在100轮一下找到方程的解,而5.95则没有找到方程的解,但是当我将5.95的结果值打印出来后,初值5.95是收敛的,直接看图。
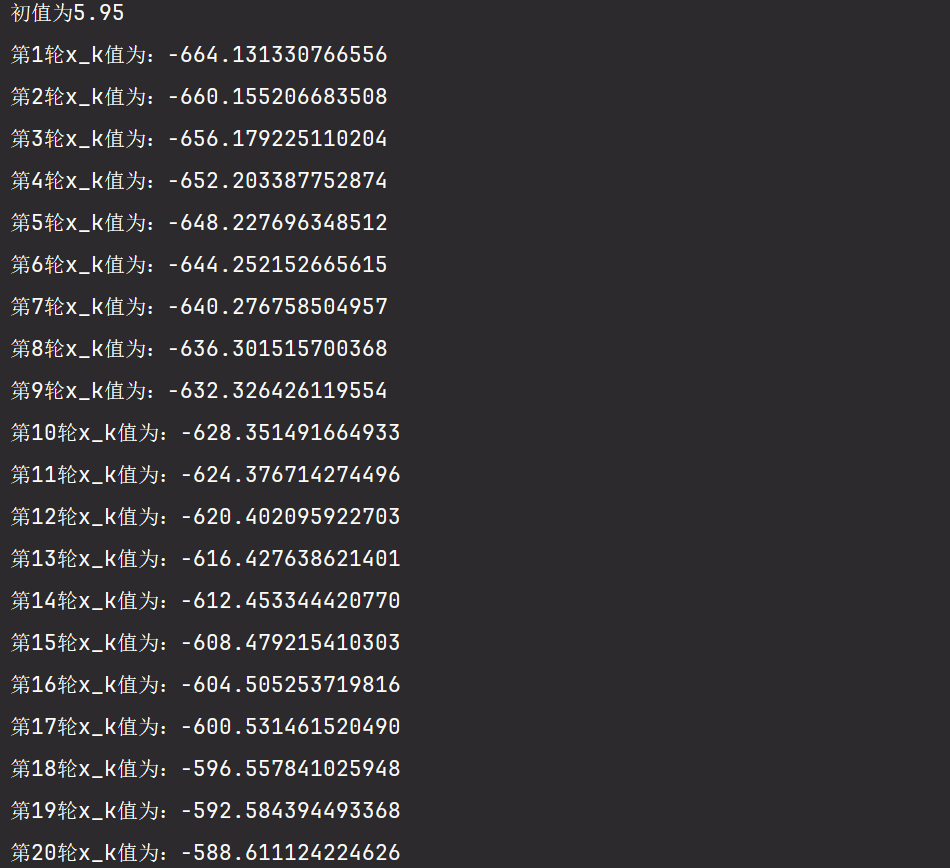
前20轮,中间省略了,太长了,直接展示后20轮
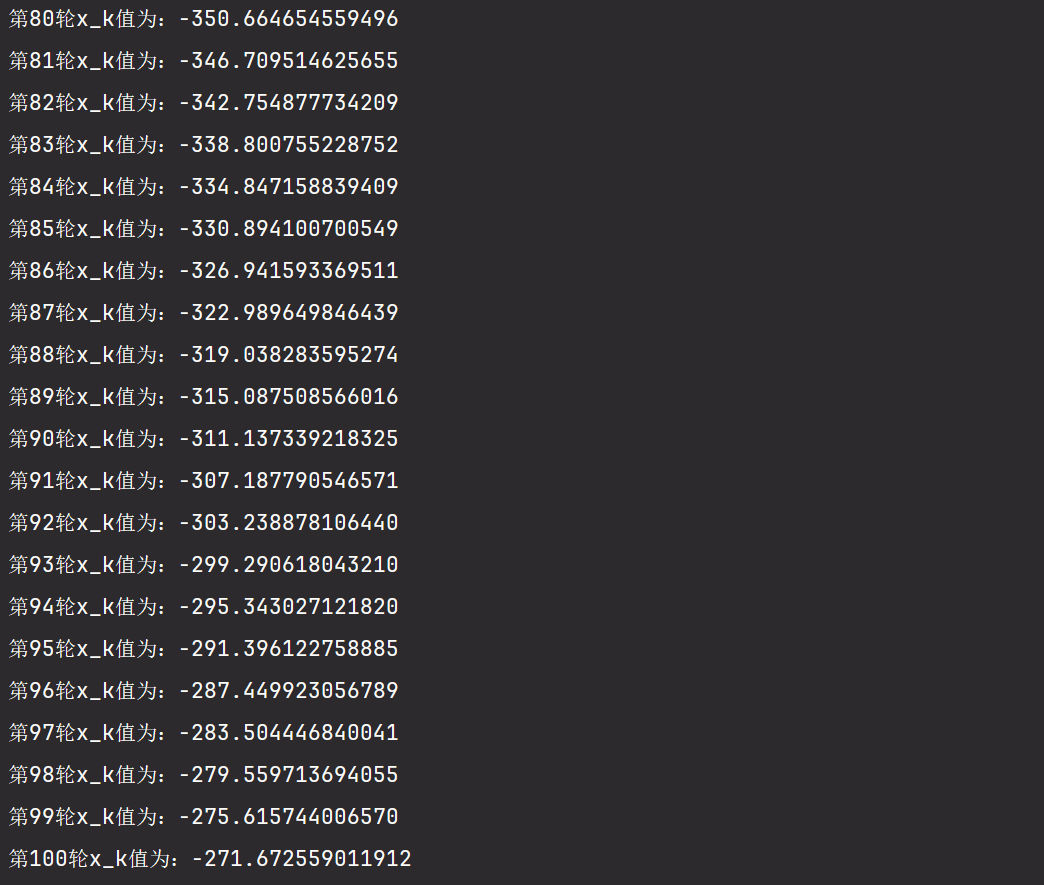
也就是说,当我的m设置得再大一点,初值5.95用牛顿迭代法就可能找到根

事实证明,在第177轮初值5.95找到了方程的根。
但遗憾的是,初值5.999999999,在经历100000轮后依旧没有找到方程的根

而在初值条件为6.0时,程序报错
![]()
也就是程序在运算的时候出现了 NAN,也就是空,原因在于在牛顿法进行迭代的时候,我们需要一阶导数作为迭代公式分母,但是在 正好是一阶导数零点,所以不能作为分母进行运算。
在初值条件为6.0000001时,程序会卡死。
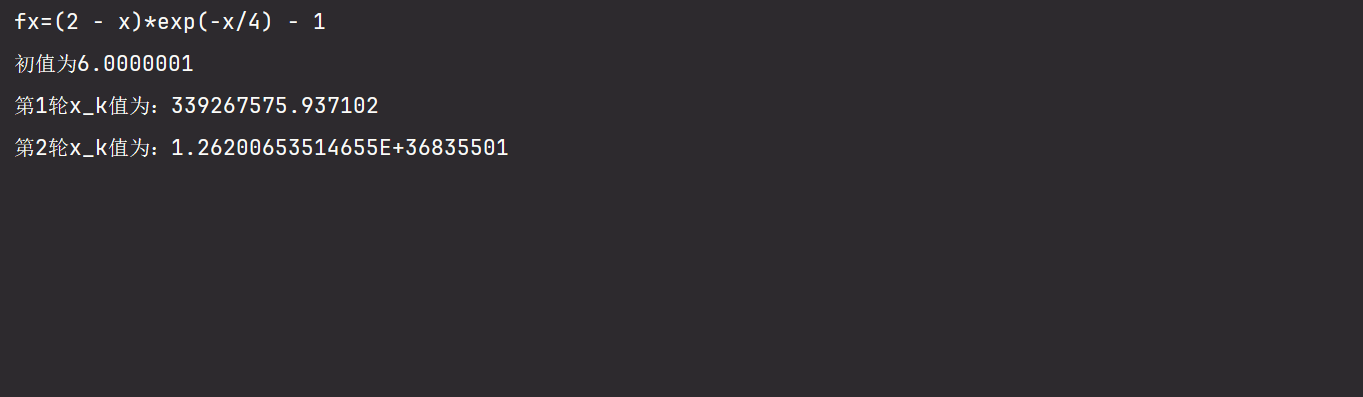
在初值条件为 6.1 的时候,程序报错
![]()
溢出错误,代表该数过大,无法继续参与云算,此时函数才算是正真意义上的发散。
在初值条件大于 6 时,其他数同理,可以试试。





















 678
678

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








