如何看待频域与时域的仿真差别

        信号与系统理论中，占空比为50%的周期信号只含有奇次谐波，实际中，时钟信号并不是理想的占空比为50%的梯形波，因此，会同时含有奇偶次谐波，一个典型的案例，如下图所示，DDR仿真中，如果用模拟的理想激励源，频谱中只会存在基频及其奇次谐波。

        利用这种自定义激励源产生的时域波形，与实测的DDR时钟信号相比，几乎看不出明显的差异，这种配置用于普通的信号仿真是没有问题的。

        但是，当使用厂商提供的IBIS驱动文件进行仿真时，从获取的频谱图中，不仅可以看到奇次谐波，还可以看到偶次谐波，说明，真实的电路行为中，时钟信号的占空比是非理想化的，频谱已经发生了变化。

        并且，通过观察实测的时钟信号频谱图，也验证了该变化的真实性，如下图所示，仿真和测试中，均发现了丰富的奇偶次谐波的存在。

        这种信号频谱的差异，不得不引起设计者的关注，因为对于常规的信号完整性仿真而言，不需要关心频谱的变化，但是，如果是评估和考察EMC/EMI问题，这种差异将会导致结果的巨大的偏差，因此，不容忽视。

        一种计算曲线边界的便捷方法是通过包络表示信号源的频谱分布，一个梯形波频谱的连续包络计算公式定义如下，频谱的单位为dBμV：

        上式中的具体定义如下：

        根据以上的公式集合，通过确定曲线中的3个频率范围，可以将连续梯形波的频谱定义如下：

        1. 当，包络为常数，等于；

        2. 当，包络等于，以斜率-20dB/dec下降；

        3. 当，包络等于，以斜率-40dB/dec下降。

        最终的时域与频域的转换效果如下图所示：

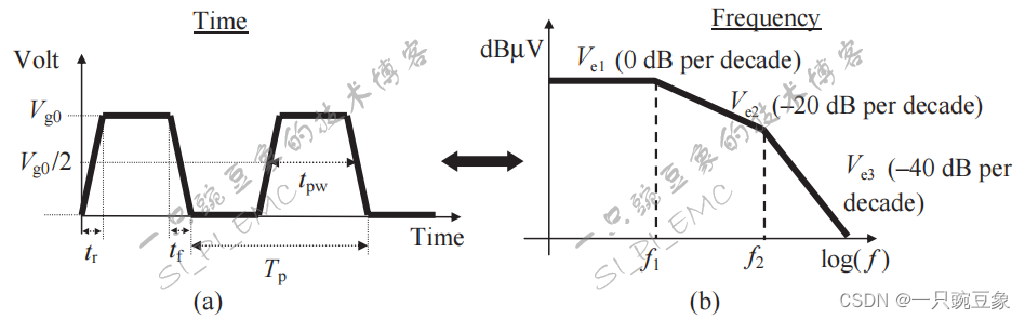
        举例来说，当Vg0=5V，tr=2ns，f=8MHz时，计算与仿真的结果完全匹配：

        因此，通过这种快速的计算方法，设计者可以较为有效地预测时钟信号的频谱分布，具有一定的设计参考价值。