Z2.3微分方程的经典解法
1.经典解

齐次解是对应齐次微分方程的解:

特征根为
2.齐次解的常用函数形式
根据不同特征根所对应的齐次解
齐次解是齐次方程中的解, 特解是原方程中的解
3.特解的常用函数形式
不同激励所对应的特解

当激励为t时的求解

4.求全解的步骤
- 通过特征方程求出特征根
- 根据特征根设出对应的齐次解
- 根据激励设出对应的特解
- 将特解代入微分方程并求解特解的未知系数
- 写出全解后根据已知条件带入求出齐次解的未知系数
Z2.4连续系统的初始值


例题

Z2.5零输入响应

零输入响应是由x,系统里的初始值产生,零状态是由输入信号产生
一个全响应就等于零输入响应+零状态响应

求解步骤
- 设定齐次解
- 代入初始值,求待定系数
一个方程左边的表达式,代表的是系统的结构
对于 零输入响应,它的初始状态的值,就是解方程的初值
 Z2.6零状态响应
Z2.6零状态响应
零状态响应的解法是齐次解+特解



提醒:写出t>0可以简化方程右边
Z2.7 响应分类
1.固有响应和强迫响应
 可以用齐次解和特解区分
可以用齐次解和特解区分
2.暂态响应和稳态响应



对四个响应的区分
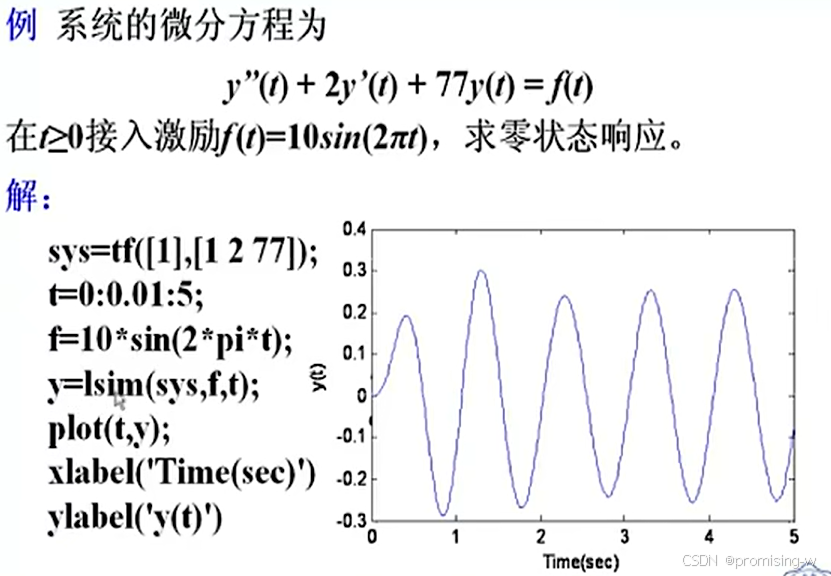
Z2.8Matlab 求解系统的响应



























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








