【数据结构C++之看懂就这一篇】二叉树（动画遍历）

已于 2024-05-12 14:09:18 修改
阅读量1k 收藏 27
点赞数 60
文章标签： 数据结构 c++ 开发语言 笔记
于 2024-05-12 07:08:39 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/2301_79682950/article/details/138702323
版权


📚博客主页：Zhui_Yi_
🔍上期回顾：队列
❤️感谢大家点赞👍🏻收藏⭐评论✍🏻，您的三连就是我持续更新的动力❤️
🎇追当今朝天骄，忆顾往昔豪杰。

在这里插入图片描述

文章目录

前言

  本篇文章会给大家讲述二叉树的知识点，包含：基本概念，性质，存储，遍历，基本操作实现，线索化二叉树，本篇文章可能包含数的一些专业术语，在这里可能不会过多解释，请见谅。文章可能会有点长，希望大家见谅，ok啊，那么我们开始今天的讲述。

一、基本概念

1.定义

二叉树的定义基本和树是类似的，但有所不同，在这里先给出：

二叉树（Binary Tree）是n（n≥0）个结点所构成的集合，它或为空树（n = 0）；或为非空树，对于非空树T：
（1）有且仅有一个称之为根的结点；
（2）除根结点以外的其余结点分为两个互不相交的子集T1和T2，分别称为T的左子树和右子树，且T1和T2本身又都是二叉树。

可能看起来有点长，但这里我解释一下，就是必须只有一个根结点，然后节点有不超过两个的分支。
记住不是每个结点都必须有两个分支，可能为：0，1，2。
如图
在这里插入图片描述

2.基本特点

结点的度小于等于2
有序树（子树有序，不能颠倒）
有以下形态：
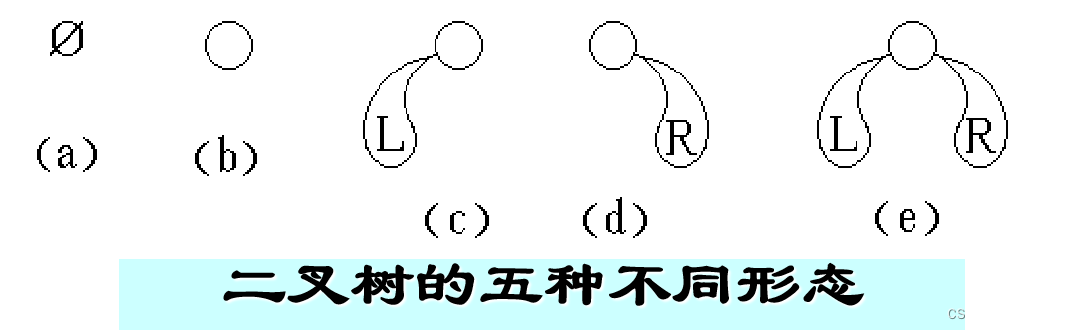
在这里插入图片描述

3.特殊形态的二叉树

①满二叉树

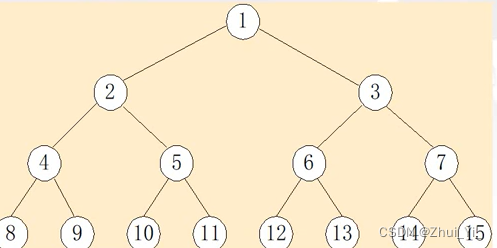
在这里插入图片描述
如图，这个二叉树有什么特点？
每个结点的度要不为0，要不为2，我们称这样的树为满二叉树。
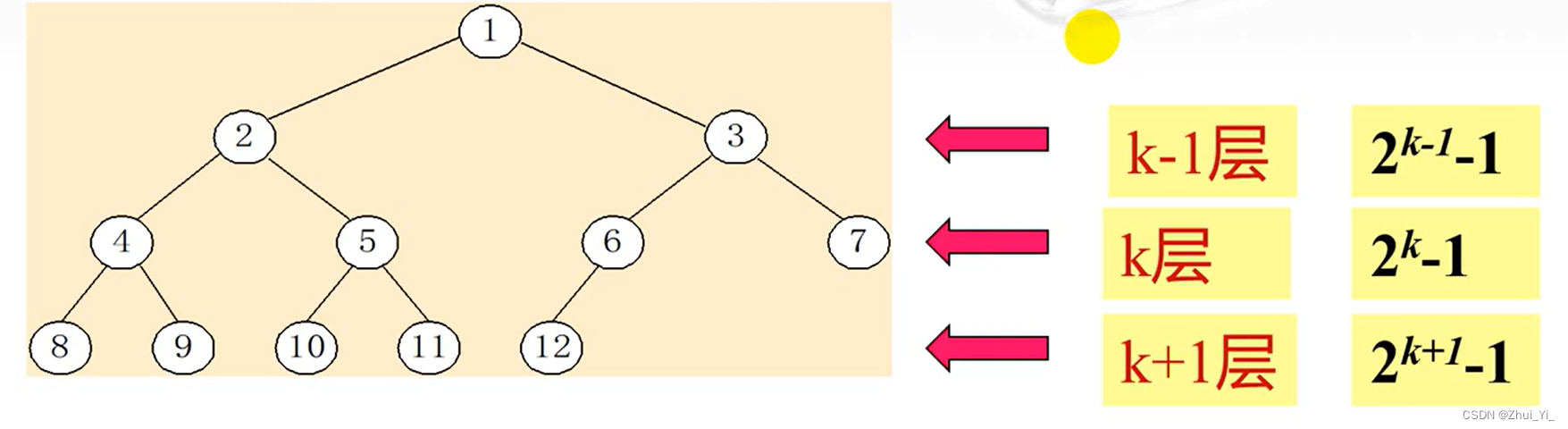
我们再来思考一下：一颗深度为k满二叉树共有多少个结点？
先看上图，

  • 深度为1的时候：节点个数为：1，21-1
  • 深度为2的时候：节点个数为：3，22-1
  • 深度为3的时候：节点个数为：7，23-1
  • 深度为4的时候：节点个数为：15，24-1

所以我们能得出一个结论：满二叉树:一棵深度为k，且有2k -1个结点的二叉树。(特点:每层都“充满”了结点)

②完全二叉树

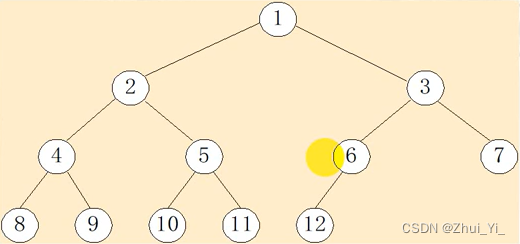
在这里插入图片描述
如上图所示，完全二叉树是一个类似于满二叉树，但又不完全是。
完全二叉树指的是：每一个结点的编号要与满二叉树对应，即出最后一层能不为空，其他层的结点必须为满，且不能只有右孩子，左孩子可存在也可以没有。
完全二叉树:深度为k的，有n个结点的二叉树，当且仅当其每个结点都与深度为k的满二叉树
中编号从1至n的结点一一对应。
可能会不懂，在这里给出一些示例，判断是不是完全二叉树：

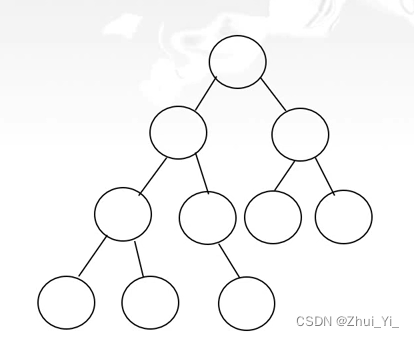
在这里插入图片描述
不是完全二叉树。为什么，如下图：
在这里插入图片描述
编号为10的在满二叉树中编号为：11
在这里插入图片描述
不是，这个过于简单，不在解释。
完全二叉树特点

  • (1)叶子结点只能在层次最大的两层上出现;
  • (2)最下层的叶子结点一定集中在左部连续位置;
  • (3)若有度为1的结点，则只可能有1个，且只能为左孩子;
  • (4)若n为奇数，则每个分支结点都有左孩子和右孩子;若n为偶数，则编号最大的分支结点(n/2) 只有左孩子，没有右孩子。

③总结

满二叉树一定是完全二叉树的，反之则不成立。

二、性质

性质1：在二叉树的第i层上至多有2i-1个结点 拓展：第i层上至少有1个结点，不可能为0，如果为0的话就不存在这一层了。
性质2: 深度为k的二叉树至多有2k-1个结点（满二叉树时） 拓展：深度为k时至少有k个结点(每一层有且仅有一个结点)
性质3:对于任何一棵二叉树，若2度的结点数有n2个，则叶子数n0必定为n2＋1 （即n0=n2+1）

对性质三给出推导：
如图：
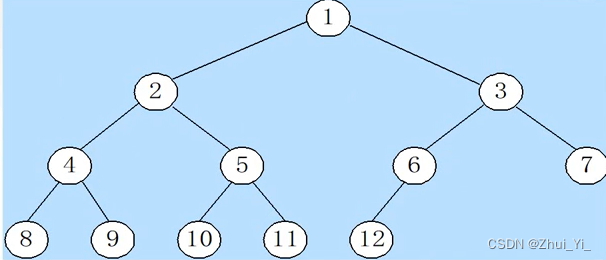
在这里插入图片描述
此时我们将双亲和孩子用线连在一起（从下往上）：
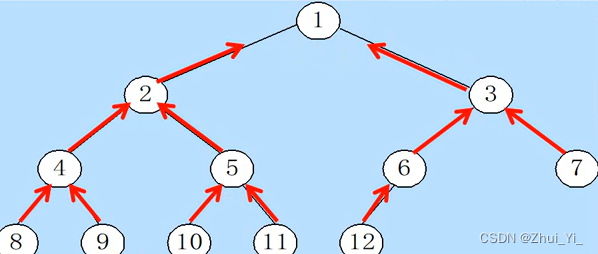
在这里插入图片描述
假设有n个结点，此时会有多少条线？
n-1条。那么此时的线的条数是不是代表该二叉树的度？
答案时肯定的。
那么我们假设度为0的个数有n0个，度为1的个数有n1个，度为2的个数有n2个，那么此时，这棵树的度数为多少？

度数=0×n0+1×n1+2×n2=n1+2n2

我们再根据我们的出的结论，度数为n-1

n-1=n1+2n2

而结点个数n又等于多少？

n=n0+n1+n2
n-1=n0+n1+n2-1
n1+2n2=n0+n1+n2-1
即：n0=n2+1

就能推出性质3了。
性质4：具有n个结点的完全二叉树的深度必为（log2n） ＋1（这里那个符号打不出来，此时括号代表的是向下取值）
推导：
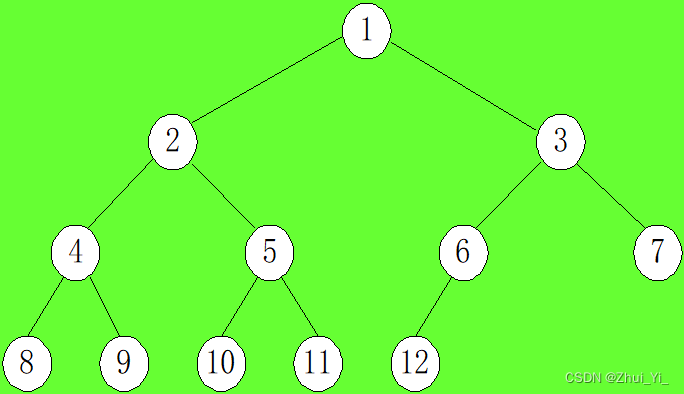
在这里插入图片描述
此时这棵树有n个结点，最后一层为第k层，那么第1层到第k-1层总共有多少个结点？

k-1层：2k-1-1个
如果当第k层填满的时候有2k-1个结点
那么第k层的第一个结点编号为：2k-1

那么就得出
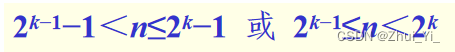
在这里插入图片描述
两边再同时取对数
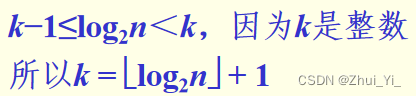
在这里插入图片描述
就得出结论。
性质5: 对完全二叉树，若从上至下、从左至右编号，则编号为i 的结点，其左孩子编号必为2i，其右孩子编号必为2i＋1；其双亲的编号必为i/2。
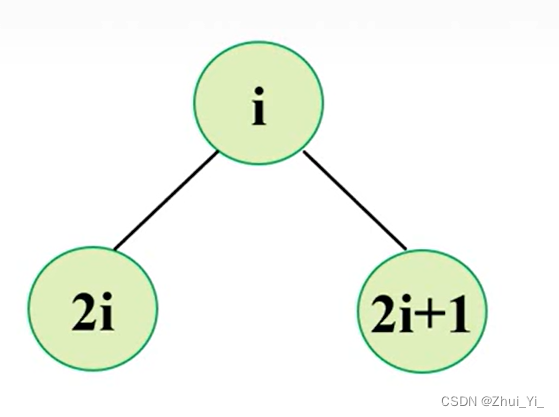
在这里插入图片描述
推导
在这里插入图片描述

三、存储结构

同样，二叉树的存储也是有两种的，一种是顺序存储，一种是链式存储。

1.顺序存储

由于顺序存储较简单，而且缺点比较明显，在这里不给出代码实现。
我们会按满二叉树的结点层次编号，依次存放二叉树中的数据元素。
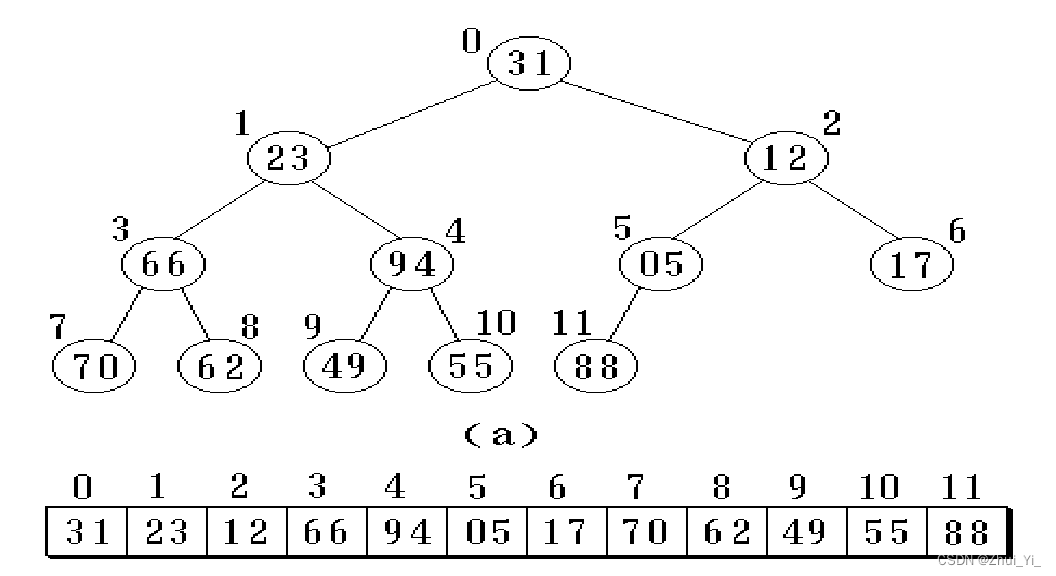
在这里插入图片描述
优点非常明显：

  1. 无需使用额外的指针或引用
  2. 访问元素效率高
  3. 存储空间利用率高
  4. 遍历方便
  5. 实现简单

但缺点也比较明显：如下图，该如何存储？
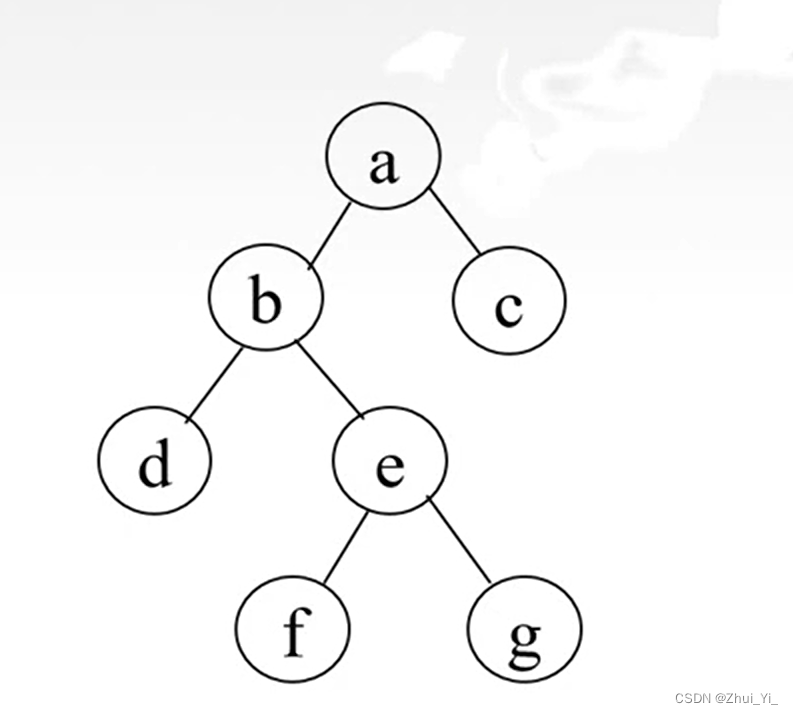
在这里插入图片描述
在这里插入图片描述
而对于单支树而言，则缺点更加明显：
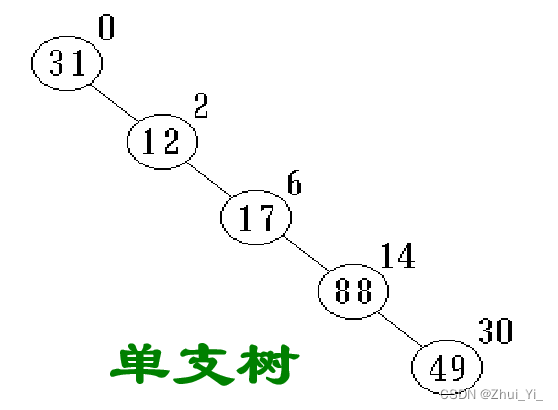
在这里插入图片描述

  1. 空间浪费
  2. 删除节点困难
  3. 动态扩展困难，顺序存储二叉树的大小是固定的，当需要插入新的节点时，如果数组已满，则需要重新分配一个更大的数组。
  4. 不适用于频繁插入和删除的场景
    顺序存储的特点就是：

结点间关系蕴含在其存储位置中
浪费空间，适于存满二叉树和完全二叉树

2.链式存储

我们要考虑一下在单链表中是如何声明的：
我们声明了指针域和数据域。其中指针域中有一个next指向下一个结点。
而在二叉树中我们需要设置几个指针？
我们考虑一下，一个节点会有几个后继？
0，1，2，而我们要保证所有的，所以要设置最多的，也就是两个指针，分别指向左孩子和右孩子。
也就是：在这里插入图片描述
这就是二叉链表
但是我们可不可以再设置一个指针，指向双亲？
可以，也就是：在这里插入图片描述
这就是三叉链表

①二叉链表

声明：

typedef struct BiNode{
   TElemType   data;
   struct  BiNode   *lchild,*rchild; //左右孩子指针
}BiTNode,*BiTree;

那么，对于下图，我们该如何用二叉链表进行存储的？
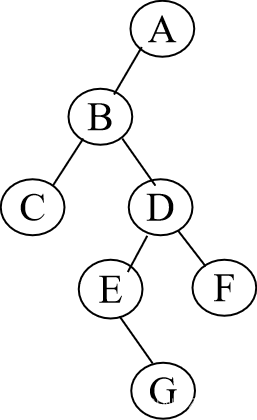
在这里插入图片描述
就是这样
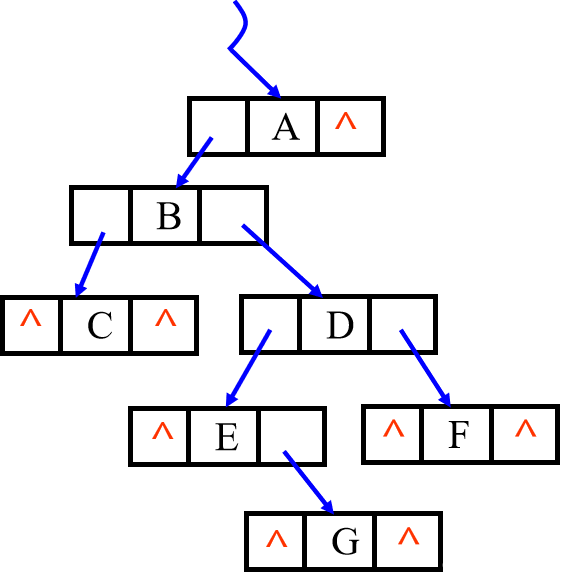
在这里插入图片描述
在n个结点的二叉链表中，有 n-1个空指针域

②三叉存储

声明：

typedef struct TriTNode{  
TelemType data;  
struct TriTNode *lchild,*parent,*rchild;
 }TriTNode,*TriTree;

它的存储方式也就是如下图：
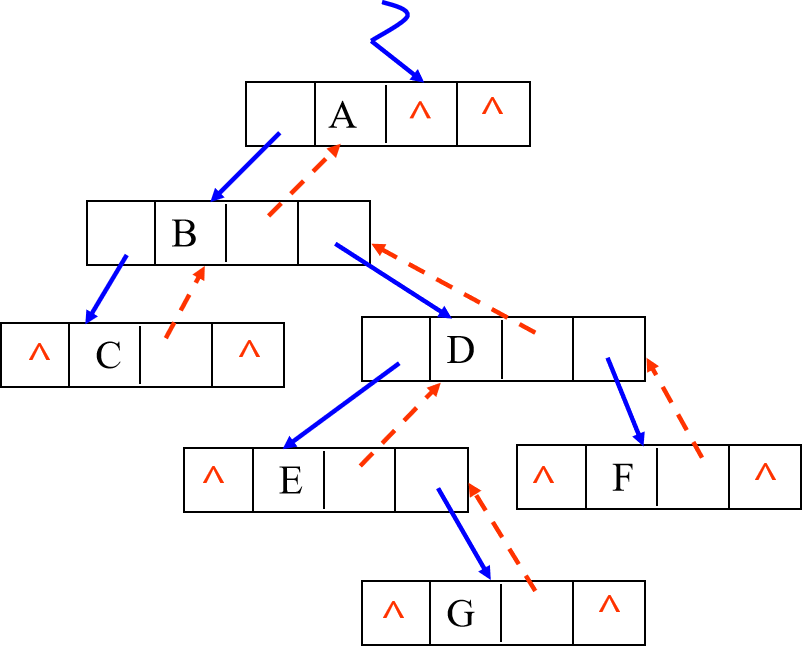
在这里插入图片描述

四、遍历二叉树（动画遍历）

引入

遍历定义：指按某条搜索路线遍访每个结点且不重复（又称周游）。
遍历用途：它是树结构插入、删除、修改、查找和排序运算的前提，是二叉树一切运算的基础和核心。
遍历的规则：
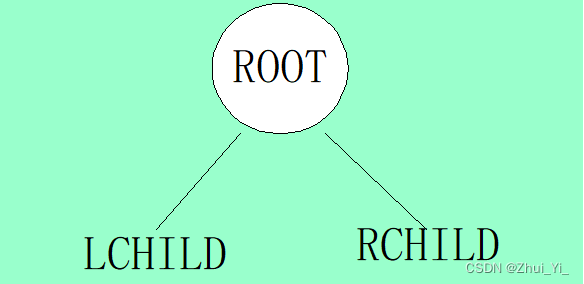
在这里插入图片描述
如图，我把ROOT简写为D，左孩子写成L，右孩子写成R：你会有几种方法将上图表示出来？
6种。分别是：DLR,LDR,LRD,DRL,RDL,RLD。
而前三种后后三种的实质是一样的，只是一个先左后右，一个先右后左，我们将采取先左后右的方式，来对遍历进行分类。
其中我们把：
DLR称为先序遍历。
LDR称为中序遍历。
LRD称为后序遍历。
还有一个层序遍历：即一层一层读，先读第一层，再度第二层，依次往后。。。。。
口诀：

DLR：先序遍历，即先根再左再右
LDR：中序遍历,即先左再根再右
LRD：后序遍历,即先左再右再根
层序：访问完一层，再访问下一层

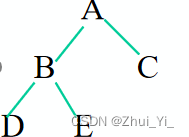
在这里插入图片描述
对于这个图片来说的话，用先序，中序，后序，层序该如何读？

先序遍历：A B D E C
中序遍历：D B E A C
后序遍历：D E B C A
层序遍历：A B C D E

1.先序遍历

按DLR形式
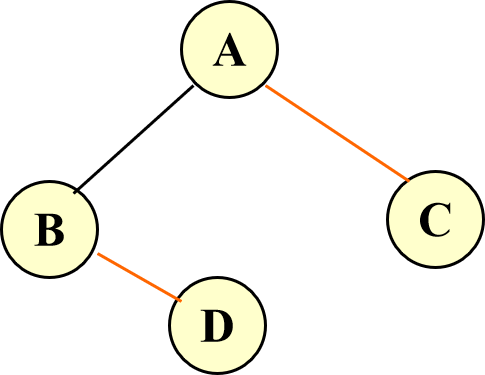
在这里插入图片描述
对于这个图片来说，按先序遍历该怎么排？
在这里插入图片描述

如图，这样遍历。
则先序遍历为：

若二叉树为空，则空操作
否则
访问根结点 (D)
前序遍历左子树 (L)
前序遍历右子树 ®

则算法实现为：

void PreOrderTraverse(BiTree T){  
  if(T == NULL) return; // 如果树为空，则直接返回  
  else {      
     cout << T->data; // 访问根结点（在遍历左、右子树之前）  
     PreOrderTraverse(T->lchild); // 递归遍历左子树  
     PreOrderTraverse(T->rchild); // 递归遍历右子树  
  }  
}

那么上述程序如何解释呢？如下图：
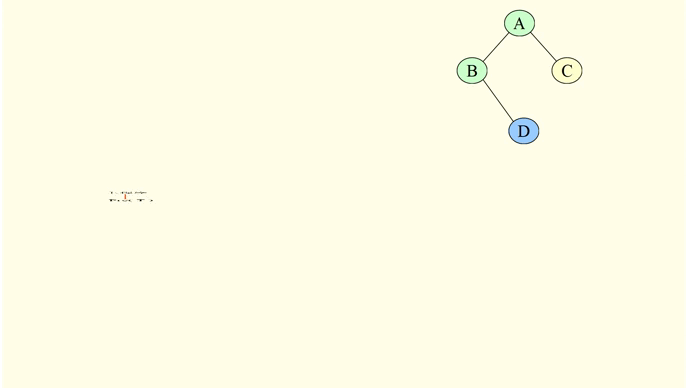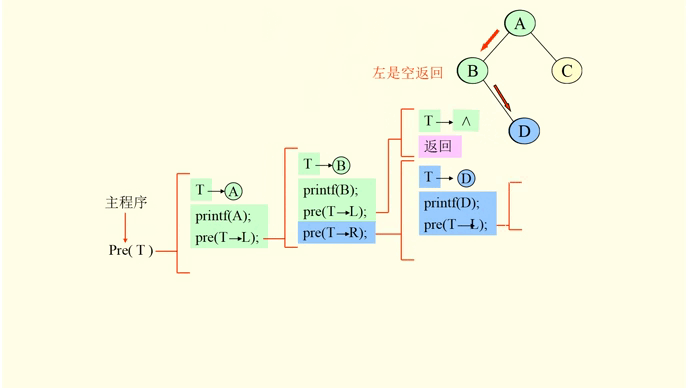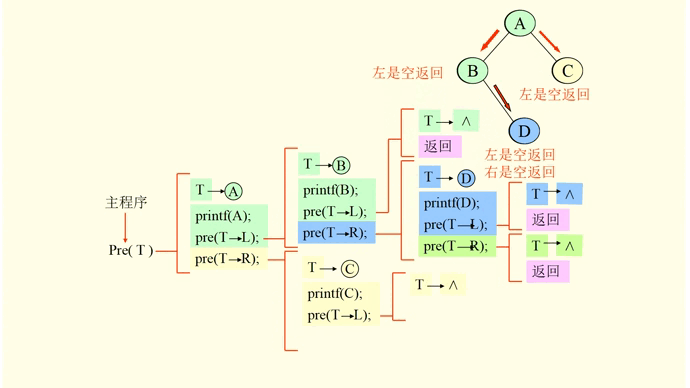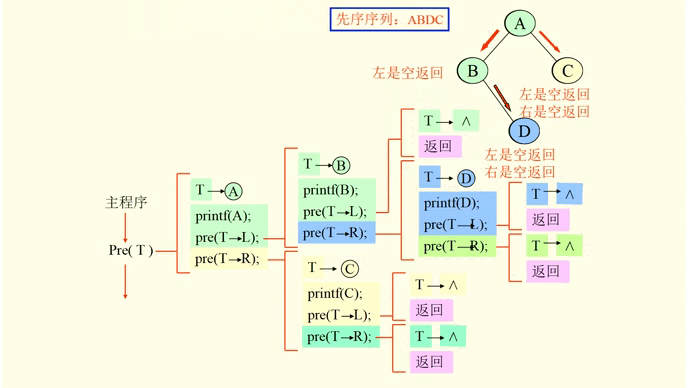
在这里插入图片描述

2,中序遍历

和先序遍历类似：
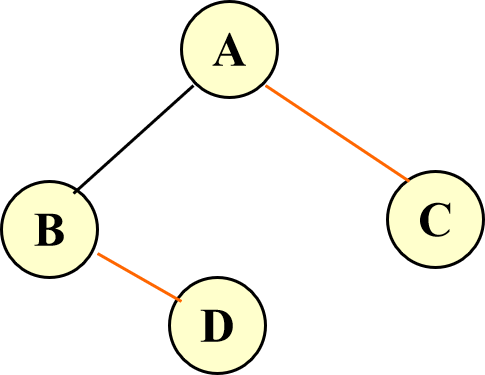
在这里插入图片描述
也是这个图片，该如何遍历

若二叉树为空，则空操作
否则:中序遍历左子树 (L)
访问根结点 (D)
中序遍历右子树 ®

在这里插入图片描述
定义：

void InOrderTraverse(BiTree T){  
  if(T == NULL) return; // 如果树为空，则直接返回  
  else {      
     InOrderTraverse(T->lchild); // 递归遍历左子树  
     cout << T->data; // 访问根结点（在遍历左子树之后）  
     InOrderTraverse(T->rchild); // 递归遍历右子树（在访问根节点之后）  
  }  
}

3.后序遍历

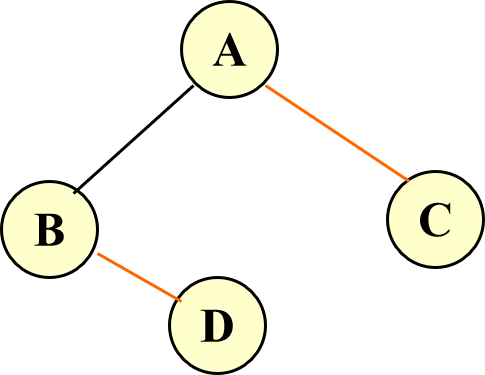
在这里插入图片描述
认识这个图片，该如何遍历？

若二叉树为空，则空操作
否则
后序遍历左子树 (L)
后序遍历右子树 ®
访问根结点 (D)

在这里插入图片描述
那么该如何定义呢？
跟前面类似：

void PostOrderTraverse(BiTree T){  
  if(T == NULL) return; // 空二叉树，直接返回  
  else{      
     PostOrderTraverse(T->lchild); // 递归遍历左子树  
     PostOrderTraverse(T->rchild); // 递归遍历右子树  
     cout << T->data; // 访问根结点（在后序遍历的最后）  
  }  
}

遍历算法的分析

我们看以上三种算法，除了访问根节点的位置不同，其他一致，也就是：

如果去掉输出语句，从递归的角度看，三种算法是完全相同的，或说这三种算法的访问路径是相同的，只是访问结点的时机不同。

我们看下图：
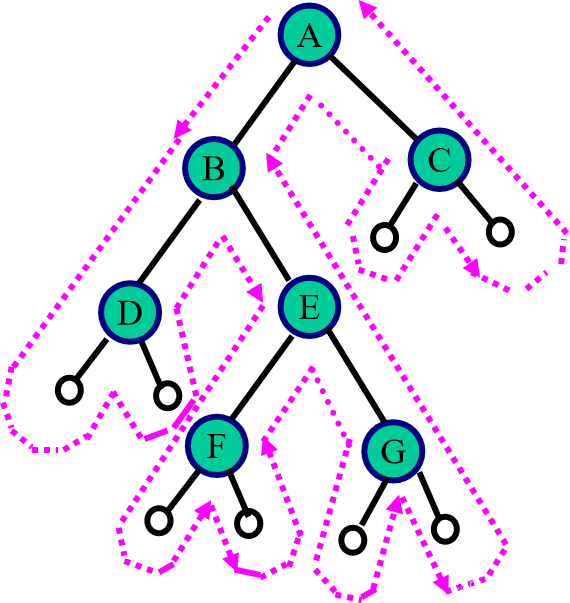
在这里插入图片描述
是从头到尾把树走完。
我们看图片，走完，虚线会经过结点几次？
3次，数一下就知道了。
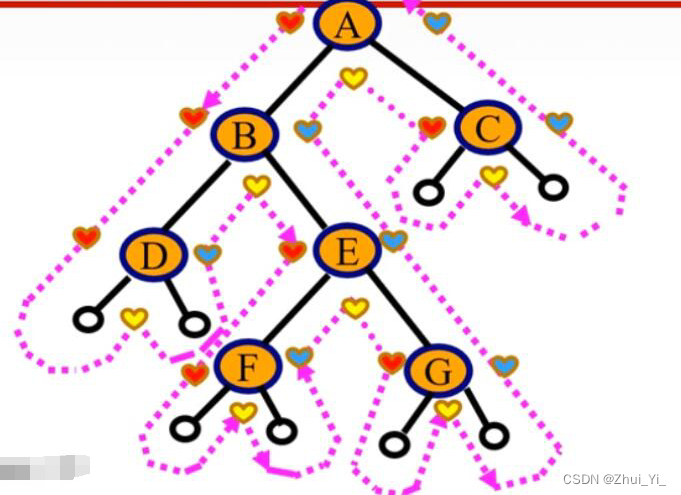
在这里插入图片描述
此时，看上图，我把第一次经过每个结点用小红心表示，第二次经过用小黄心，第三次经过用小蓝心。
然后，我们按照顺序读一下：

第一次：A B D E F G C
第二次：D B F E G A C
第三次：D F G E B C A

我们看能不能根据前面几种遍历来推出规律？

第1次经过时访问＝先序遍历
第2次经过时访问＝中序遍历
第3次经过时访问＝后序遍历

至于各个复杂度：

时间效率:O(n) //每个结点只访问一次
空间效率:O(n) //栈占用的最大辅助空间

重要结论

若二叉树中各结点的值均不相同，则：
由二叉树的前序序列和中序序列，或由其后序序列和中序序列，或有其层序序列和中序序列均能唯一地确定一棵二叉树，
但由前序序列和后序序列却不一定能唯一地确定一棵二叉树。

或许不懂，但我给出一个练习题我们可以试一下：

已知一棵二叉树的中序序列和后序序列分别是BDCEAFHG 和 DECBHGFA，请画出这棵二叉树。

我们如何推，可以根据各个遍历的结论来推：

①由后序遍历特征，根结点必在后序序列尾部（A）；
②由中序遍历特征，根结点必在其中间，而且其左部必全部是左子树子孙（BDCE），其右部必全部是右子树子孙（FHG）；
③继而，根据后序中的DECB子树可确定B为A的左孩子，根据HGF子串可确定F为A的右孩子；以此类推。

如下图：
在这里插入图片描述

五、基本操作的实现（链式存储）

以二叉链表为例。

前情回顾

我们是如何声明二叉树的？

typedef struct BiNode{
   TElemType   data;
   struct  BiNode   *lchild,*rchild; //左右孩子指针
}BiTNode,*BiTree;

①建立二叉树

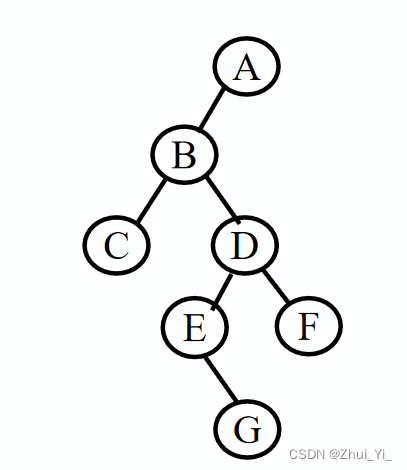
在这里插入图片描述
如上图，如果我们使用先序遍历的话该如何输入？
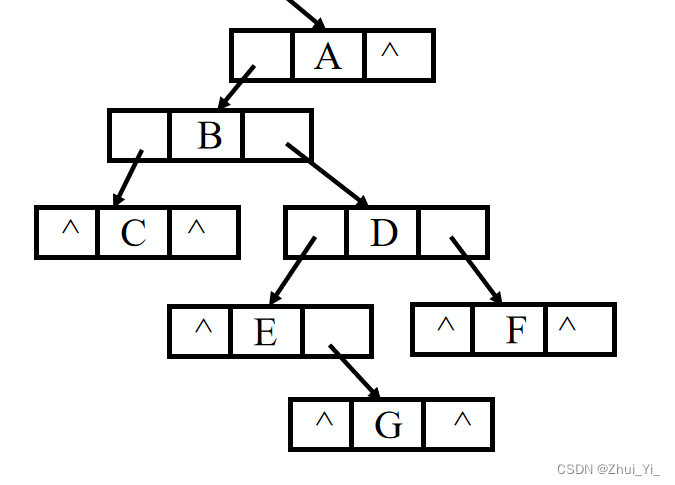
在这里插入图片描述
先看图片，先序遍历就该这样表示，也就是这样输入。(其中^代表空)

A B C ^ ^ D E ^ G ^ ^ F ^ ^ ^

那么该怎么用算法实现呢？
我们先考虑，我们肯定要先输一个内容，然后再来判断是不是为空，如果为空的话，是不是要返回上一个结点，如果不为空，要把此内容输入到结点中去，然后再跳到下一个节点去。那么可以用什么来实现呢？
递归。
那么该如何用程序来实现？

void CreateBiTree(BiTree& T) {
    char ch;
    cin >> ch;
    if (ch == '#') {
        T = NULL;  // 递归结束，建空树  
    }
    else {
        T = new BiTNode;  // 生成根结点  
         T->data = ch;
        CreateBiTree(T->lchild);  // 递归创建左子树  
        CreateBiTree(T->rchild); // 递归创建右子树  
    }
}

上述可用下图表示：
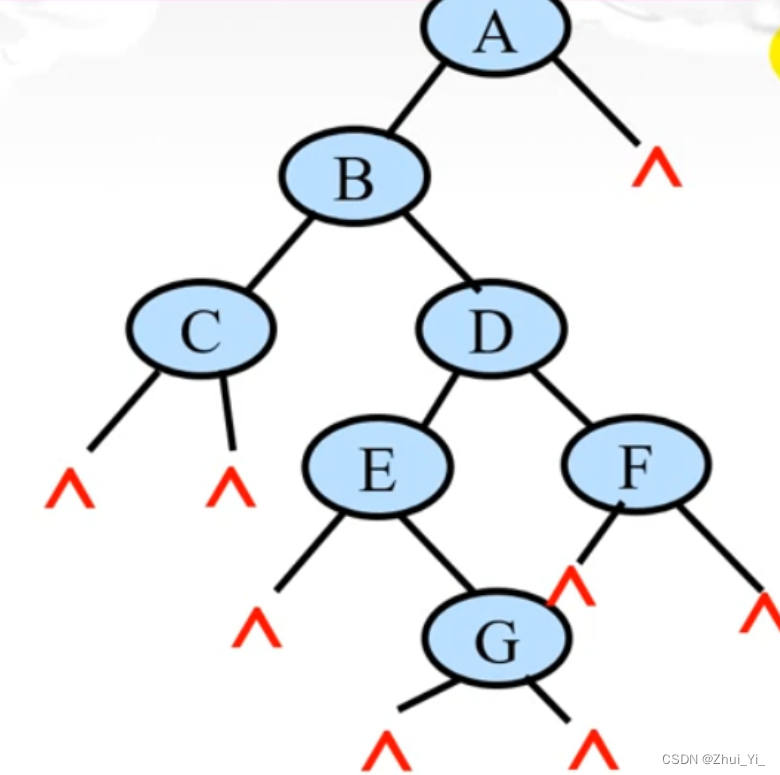
在这里插入图片描述
那我们考虑一下如何用中序和后序来进行建立呢？
是不是跟遍历一样呢？
答案是肯定的，只需要变换T-＞data=ch的位置，就可以来写出中序和后序了，在这里不过多阐述。直接给出程序

void CreateBiTreeInOrder(BiTree &T) {
    cin >> ch;
    if (ch == '#') {
        T = NULL;
    } else {
        T = new BiTNode;
        CreateBiTreeInOrder(T->lchild);
        T->data = ch;
        CreateBiTreeInOrder(T->rchild);
    }
}

void CreateBiTreePostOrder(BiTree &T) {
    cin >> ch;
    if (ch == '#') {
        T = NULL;
    } else {
        T = new BiTNode;
        CreateBiTreePostOrder(T->lchild);
        CreateBiTreePostOrder(T->rchild);
        T->data = ch;
    }
}

②复制

复制其实跟建立差不多，只不过是把原二叉树的值赋给另一个二叉树，直接给出程序：

void Copy(BiTree T, BiTree &NewT){
if(T== NULL) {
NewT=NULL;
return; }
else {NewT=new BiTNode; 
NewT->data=T->data;
Copy(T->lchild,NewT->lchild);
Copy(T->rchild,NewT->rchild); }

中序和后序只需改变一下位置，在这里不在给出。

③计算二叉树结点总数

有两种情况：
一种是空树，结点总数直接为0.
一种是不为空，结点数等于多少？
我们考虑一下，结点数是不是度为0的+度为1的+度为2的，但是我们又无法知道，我们可以转换一下？
度为0的是不是代表它没有子树，度为1的是不是代表它有左子树或者右子树，度为2的是不是代表它有左子树和右子树，那这不是很简单吗？
但是我们好像忽视了一个问题？
根节点是谁的子树？
谁的都不是，那么我们是不是要在最后加上1。
故，得出结论

如果是空树，则结点个数为0；
否则，结点个数为左子树的结点个数+右子树的结点个数再+1。

程序实现如下：

int NodeCount(BiTree T){
  if(T == NULL ) return 0;  
  else return NodeCount(T->lchild)+NodeCount(T->rchild)+1;
}

④计算二叉树叶子结点总数

也有两种情况：
一种为空树，叶子节点总数为0
一种不为空，那叶子结点总数应该为多少呢？
我们要考虑一下什么是叶子节点？
度为0的，它们没有子节点，只有一个父节点。
那么就好说了，只要一个结点的左子树和右子树为空，我们就+1。
得结论：

如果是空树，则叶子结点个数为0；
否则，为左子树的叶子结点个数+右子树的叶子结点个数。

程序实现：

int LeafCount(BiTree T){
 	if(T==NULL) 	//如果是空树返回0
		return 0;
	if (T->lchild == NULL && T->rchild == NULL)
		return 1; //如果是叶子结点返回1
	else return LeafCount(T->lchild) + LeafCount(T->rchild);
}

⑤计算二叉树深度

也有两种情况：
空树，深度为0
不为空，该如何计算？
我们是不是求到左子树的尽头，再求到右子树的尽头，然后判断哪个大，再加上根所在的，返回。
得结论：

如果是空树，则深度为0；
否则，递归计算左子树的深度记为m，递归计算右子树的深度记为n，二叉树的深度则为m与n的较大者加1。

代码实现如下：

int Depth(BiTree T){
if(T== NULL)
return 0;
else { 
int m=Depth(T->lchild); 
int n=Depth(T->rchild);
if(m>n) 
return m+1;
else
return n+1 ;
}
}

主程序

建立下图二叉树
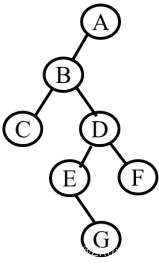
在这里插入图片描述

#include <iostream>
using namespace std;
typedef char TElemType;
typedef struct BiNode {
	TElemType   data;
	struct  BiNode* lchild, * rchild; //左右孩子指针
}BiTNode, * BiTree;
//先序
void CreateBiTree(BiTree& T) {
    char ch;
    cin >> ch;
    if (ch == '#') {
        T = NULL;  // 递归结束，建空树  
    }
    else {
        T = new BiTNode;  // 生成根结点  
        T->data = ch;
        CreateBiTree(T->lchild);  // 递归创建左子树  
        CreateBiTree(T->rchild); // 递归创建右子树  
    }
}
//先序遍历
void PreOrderTraverse(BiTree T) {
    if (T == NULL) return; // 如果树为空，则直接返回  
    else {
        cout << T->data; // 访问根结点（在遍历左、右子树之前）  
        PreOrderTraverse(T->lchild); // 递归遍历左子树  
        PreOrderTraverse(T->rchild); // 递归遍历右子树  
    }
}
//中序遍历
void InOrderTraverse(BiTree T) {
    if (T == NULL) return; // 如果树为空，则直接返回  
    else {
        InOrderTraverse(T->lchild); // 递归遍历左子树  
        cout << T->data; // 访问根结点（在遍历左子树之后）  
        InOrderTraverse(T->rchild); // 递归遍历右子树（在访问根节点之后）  
    }
}
//后序遍历
void PostOrderTraverse(BiTree T) {
    if (T == NULL) return; // 空二叉树，直接返回  
    else {
        PostOrderTraverse(T->lchild); // 递归遍历左子树  
        PostOrderTraverse(T->rchild); // 递归遍历右子树  
        cout << T->data; // 访问根结点（在后序遍历的最后）  
    }
}
//计算深度
int Depth(BiTree T) {
    if (T == NULL)
        return 0;
    else {
        int m = Depth(T->lchild);
        int n = Depth(T->rchild);
        if (m > n)
            return m + 1;
        else
            return n + 1;
    }
}
//结点的总数
int NodeCount(BiTree T) {
    if (T == NULL) return 0;
    else return NodeCount(T->lchild) + NodeCount(T->rchild) + 1;
}
//叶子节点
int LeafCount(BiTree T) {
    if (T == NULL) 	//如果是空树返回0
        return 0;
    if (T->lchild == NULL && T->rchild == NULL)
        return 1; //如果是叶子结点返回1
    else return LeafCount(T->lchild) + LeafCount(T->rchild);
}
int main() {

    BiTree T;

    CreateBiTree(T);

    cout << "先序：";

    PreOrderTraverse(T);

    cout << endl;

    cout << "中序：";

    InOrderTraverse(T);

    cout << endl;

    cout << "后序：";

    PostOrderTraverse(T);

    cout << endl;

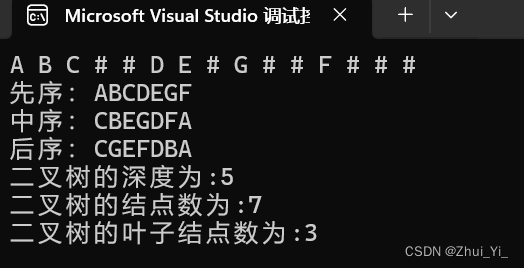
    cout << "二叉树的深度为:" << Depth(T) << endl;

    cout << "二叉树的结点数为:" << NodeCount(T) << endl;

    cout << "二叉树的叶子结点数为:" << LeafCount(T) << endl;

    return 0;

}

#

六、线索化二叉树

提示

只给一些定义，不给程序实现。

引入

为什么要提出线索化二叉树
我们在前面提到过：

在n个结点的二叉链表中，有n+1个空指针域

会造成空间的浪费？
二叉链表空间效率这么低，能否利用这些空闲区存放有用的信息或线索？
我们可以可以用它来存放当前结点的直接前驱和后继等线索，以加快查找速度。
由此便提出了线索化二叉树。

普通二叉树只能找到结点的左右孩子信息，而该结点的直接前驱和直接后继只能在遍历过程中获得。
若将遍历后对应的有关前驱和后继预存起来，则从第一个结点开始就能很快“顺藤摸瓜”而遍历整个树。

那我们该如何保存结点的前驱和后继信息呢？

  1. 增加两个域：fwd和bwd；
  2. 利用空链域（n+1个空链域）

我们采用利用空链域。

线索化二叉树

我们如果增加两个域的话，如果有孩子的话可以指向孩子，如果没孩子的话是不是又造成空间的浪费了?
那我们就可以没左孩子指向其前驱，没有孩子指向其后继。即：

若结点有左子树，则lchild指向其左孩子；
否则， lchild指向其直接前驱(即线索)；
若结点有右子树，则rchild指向其右孩子；
否则， rchild指向其直接后继(即线索) 。

但我们可能会出现混淆，不知道该指向那个？
为了避免混淆，增加两个标志域即如下图：
在这里插入图片描述
那么我们该如何利用这两个标志域来区分它们是否有孩子或前驱后继？

LTag :若 LTag=0, lchild域指向左孩子； 若 LTag=1, lchild域指向其前驱。
RTag :若 RTag=0, rchild域指向右孩子； 若 RTag=1, rchild域指向其后继。

其实质就是：

线索二叉树的的实质:
将二叉链表中的空指针改为指向前驱/后继的线索，即在遍历过程中修改空指针的过程。

相关术语

线索：指向结点前驱和后继的指针
线索链表：加上线索的二叉链表
线索二叉树：加上线索的二叉树（图形式样）
线索化：对二叉树以某种次序遍历使其变为线索二叉树的过程

先序线索二叉树

先序线索化即利用先序遍历来读。
如下图：
在这里插入图片描述
用先序遍历该如何表示？
首先我们要读出先序序列：ABCDE，然后再写出每个结点的关系：

  • 对于A来说：其有左子树和右子树，所以LTag=RTag=0,其左孩子为B,右孩子为D
  • 对于B来说，其只有右子树，所以LTag=1,RTag=0,根据先序序列，其前驱为A；右孩子为C
  • 对于D来说，其只有左子树，所以LTag=0,RTag=1,其左孩子为E；根据先序序列，其后继也为E
  • 对于C来说，其没有左子树和右子树，所以LTag=RTag=1,根据先序序列，其前驱为B，后继为D
  • 对于E来说，其没有左子树和右子树，所以LTag=RTag=1,根据先序序列，其前驱为D后继为空

在这里插入图片描述
根据图片，D是无法直接找到前驱。

中序线索二叉树

首先我们要先读出中序序列：BCAED，然后再写出关系：

  • 对于A来说：其有左子树和右子树，所以LTag=RTag=0,其左孩子为B,右孩子为D
  • 对于B来说，其只有右子树，所以LTag=1,RTag=0,根据中序序列，其前驱为空；右孩子为C
  • 对于D来说，其只有左子树，所以LTag=0,RTag=1,其左孩子为E；根据中序序列，其后继为空
  • 对于C来说，其没有左子树和右子树，所以LTag=RTag=1,根据中序序列，其前驱为B，后继为A
  • 对于E来说，其没有左子树和右子树，所以LTag=RTag=1,根据中序序列，其前驱为A，后继为D

在这里插入图片描述
结点前驱、后继均可访问到

后序线索二叉树

首先我们要读出后序序列：CBEDA

  • 对于A来说：其有左子树和右子树，所以LTag=RTag=0,其左孩子为B,右孩子为D
  • 对于B来说，其只有右子树，所以LTag=1,RTag=0,根据后序序列，其前驱为C；右孩子为C
  • 对于D来说，其只有左子树，所以LTag=0,RTag=1,其左孩子为E；根据后序序列，其后继为A
  • 对于C来说，其没有左子树和右子树，所以LTag=RTag=1,根据后序序列，其前驱为空，后继为B
  • 对于E来说，其没有左子树和右子树，所以LTag=RTag=1,根据后序序列，其前驱为B，后继为D

在这里插入图片描述
B无法访问到后继

例题

画出以下二叉树对应的中序线索二叉树。
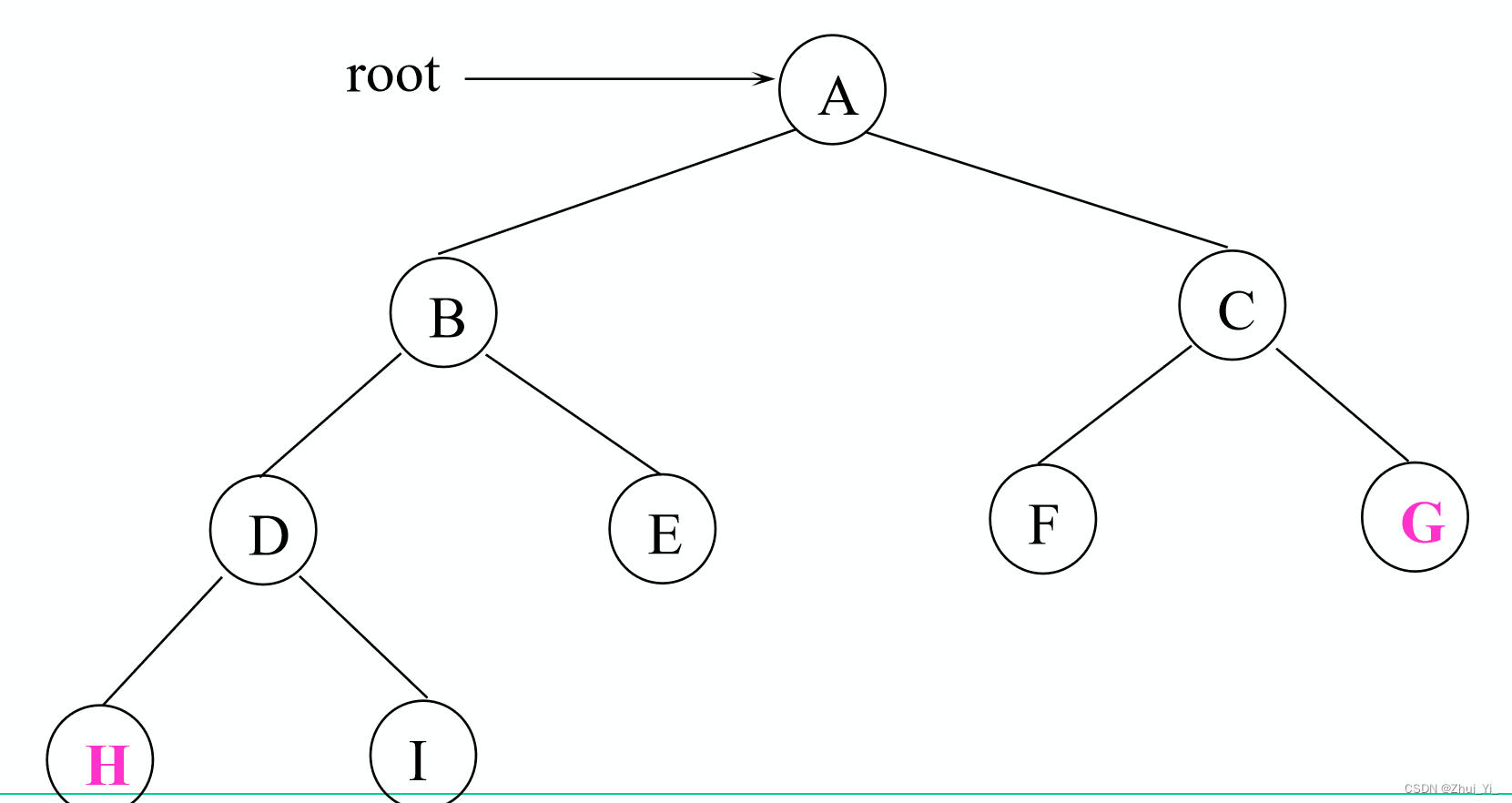
在这里插入图片描述
首先我们先写出中序序列：H, D, I, B, E, A, F, C, G
然后再画出:
在这里插入图片描述

补充

先序线索二叉树查找后继:
有左孩子- >左孩子为后继
只有右孩子>右孩子为后继
无左右孩子>右指针指向后继

中序线索二叉树查找前驱与后继:
有左右孩子>左下最靠右为前驱，右下最靠左为后继

后序线索二叉树查找前驱:
有右孩子/左右孩子>右孩子为前驱
只有左孩子>左孩子为前驱
无左右孩子>左指针指向前驱

总结

快乐的时光总是短暂的，文章到这里就结束了，本篇文章详细的写出了二叉树的一些知识点，欢迎大家前来指正！！！

Zhui_Yi_
关注
  • 60
    点赞
  • 踩
  • 27
    收藏
    觉得还不错? 一键收藏
  • 21
    评论
数据结构C++二叉树的先序遍历、中序遍历和后序遍历实现
12-06
数据结构C++二叉链表的先序遍历、中序遍历和后序遍历实现
C语言数据结构之线索二叉树及其遍历
08-29
主要介绍了C语言数据结构之线索二叉树及其遍历的相关资料,为了加快查找节点的前驱和后继。对二叉树的线索化就是对二叉树进行一次遍历，在遍历的过程中检测节点的左右指针是否为空，如果是空，则将他们改为指向前驱和后继节点的线索，需要的朋友可以参考下
数据结构课程设计报告-二叉树的遍历.docx
03-07
数据结构课程设计报告-二叉树的遍历.docx
数据结构二叉树的遍历 二叉树的深度 二叉树的某结点层次 二叉树结点数
08-27
数据结构二叉树的遍历 二叉树的深度 二叉树的某结点层次 二叉树结点数
C++数据结构与算法二叉树的层序遍历代码及注释
04-02
C++数据结构与算法二叉树的层序遍历代码及注释
别再翻了，面试二叉树看这 11 个就够了~
热门推荐
小鹿动画学编程
09-13 12万+
写在前边 数据结构与算法： 不知道你有没有这种困惑，虽然刷了很多算法题，当我去面试的时候，面试官让你手写一个算法，可能你对此算法很熟悉，知道实现思路，但是总是不知道该在什么地方写，而且很多边界条件想不全面，一紧张，代码写的乱七八糟。如果遇到没有做过的算法题，思路也不知道从何寻找。面试吃了亏之后，我就慢慢的做出总结，开始分类的把数据结构所有的题型和解题思路每周刷题做出的系统性总结写在了 Github...
【数据结构】十大排序
英雄哪里出来
01-11 7万+
打开算法大门，从排序开始
超硬核十万字！全网最全 数据结构 代码，随便秒杀老师/面试官，我说的
hebtu666
04-20 10万+
本文代码实现基本按照《数据结构》课本目录顺序，外加大量的复杂算法实现，一篇文章足够。能换你一个收藏了吧？
C++八股文分享---数据结构其一---树（二叉树、二叉搜索树、AVF树、红黑树、B树与B+树、赫夫曼树）
weixin_41776007的博客
04-17 1288
八股文分享 — 数据结构树（二叉树、二叉搜索树、AVL树、红黑树、B树与B+树） #前言 树是一种非常典型的数据结构，无论是面试还是对于日常开发来讲，都是一个应该理解透彻的数据结构。部分树应该掌握到可手撕，较复杂的树应知道内部实现原理。本文需要对树结构有一定了解，不会细致的分享每一种数据结构的基础知识，只分享我在复习过程中认为重要的知识点。 一、二叉树 二叉树的特点为任意节点至多有2个孩子子节点。对于二叉树，我们要掌握如下知识点： 1、二叉树的前序遍历、中序遍历、后序遍历： 三种遍历的思路相同使用递归实现
课程设计报告数据结构二叉树遍历演示_二叉树中序遍历怎么看
01-08
课程设计报告数据结构二叉树遍历演示
山东建筑大学计算机学院数据结构实验二：二叉树的遍历
03-31
1、用先序方法建立一棵二叉树； 2、实现先序、中序和后序遍历二叉树的操作； 3、实现统计二叉树叶子结点个数和计算二叉树深度的操作； 要求： 1、二叉链表结点类的定义； 2、二叉树类的定义； 3、创建一棵二叉树： 4、实现输出以上二叉树先序、中序和后序遍历序列中第k个数据元素的操作； 5、判断二叉树是否是完全二叉树； //先序遍历递归算法 public void preRootTraverse(BiTreeNode T){ if(T != null){ System.out.print(T.data); preRootTraverse(T.lchild); preRootTraverse(T.rchild); } }
JavaScript数据结构之二叉树的遍历算法示例
10-20
主要介绍了JavaScript数据结构之二叉树的遍历算法,简单介绍了javascript实现数据结构中二叉树的中序遍历、先序遍历及后序遍历方法与相关使用技巧,需要的朋友可以参考下
C/C++数据结构实现二叉树的遍历与线索二叉树
12-26
使用C/C++实现二叉树的构造、先序遍历、中序遍历、后序遍历、中序线索化、线索化后的中序遍历等基本树操作。
代码随想录第十四天|理论基础、二叉树的递归遍历、二叉树的迭代遍历、二叉树的统一迭代法
suanheuo的博客
11-15 110
二叉树基础
二叉树的建立，输出，深度，宽度与最大宽度，节点总数，叶子节点数，删除，c/c++描述
zhangzhangkeji的博客
06-10 809
  内容来自课本例题。通过总结，学会得更深入一点，才便于记忆。   二叉树的建立，函数createBTree，课本采用栈的方法，和二叉树的逗号表达式是匹配的。详细分析，见上篇   二叉树的输出，函数displayBTree，采用递归方法，遇到子节点，则开始输出左括号。详细见上篇。   二叉树的深度：函数depthBiTree，其递归定义是左右子节点的较大深度加1.这也是函数该函数的编程思想，空节点深度为0，无子节点的节点深度为1。   查找二叉树里某一节点，函数findNode，返回指向该节点的指针。递归思
小学生C++编程启蒙
青少年趣味编程
11-22 3256
小学生C++编程启蒙
[力扣刷题总结]（二叉树篇）
weixin_38800498的博客
12-29 1335
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录二叉树理论基础篇1.二叉树的种类2.二叉树的存储方式3.二叉树的遍历方式4.二叉树的定义////////////二叉树的遍历方式///////////////二叉树的递归遍历二叉树的迭代遍历1. 迭代法中序遍历2.迭代法前序遍历3.迭代法后序遍历144. 二叉树的前序遍历解法1：递归遍历解法2：迭代遍历二叉树的层序遍历////////////二叉树的属性///////////////////////////二叉树的修改与改造////
数据结构：模拟队列
最新发布
weixin_43790371的博客
05-30 189
【代码】【无标题】
数据结构二叉树先序遍历
10-24
二叉树是一种常见的数据结构，它由节点和边组成，每个节点最多有两个子节点，分别称为左子节点和右子节点。二叉树的先序遍历是指先访问根节点，然后按照先左后右的顺序遍历左右子树。具体实现可以使用递归或者栈来...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 21
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值