第四周：CFD基础理论学习+Ansys fluent 实例操作

摘要

  本周主要学习了CFD的基础理论知识和进行了Ansys fluent 的某注射器的内流场网格划分实例操作，包括如何划分面网格，对进出口进行封口从而捕捉流体在注射器中运动的位置，设置边界层以便于精确分析流体在装置中的状态，到最后的体网格生成。对于CFD基础，学习了何为N-S方程、控制方程、如何计算流通量和偏微分方程的分类及特征。

Abstract

In this week，I mainly learned about the basic theory of CFD and the internal flow field meshing example of an Ansys fluent syringe.including how to divide the surface mesh, seal the inlet and outlet to capture the position of the fluid movement in the syringe, set the boundary layer to accurately analyze the state of the fluid in the device, and finally generate a volume mesh. For the basics of CFD, learned what is the N-S equation, the control equation, how to calculate the flow rate, and the classification and characteristics of partial differential equations.

CFD基础

1.基本概念

 CFD为通过离散求解流动方程的信息，在计算流体力学（CFD）中，往往使用有限差分法和有限体积法来进行计算。有限差分法的精度较高，但处理复杂网格不够灵活，适用与处理简单网格，但关于流体的流动状态可以进行复杂变化，类似与一阶的泰勒展开，精度为一阶。有限体积法则与其相反，适用与处理求解复杂网格，即将空间视为三维进行泰勒展开，精度为二阶。

2.基本方程组

  由于流场状态不好分析，往往观察对象设成在微观上充分大，宏观上充分小的流体质点。通常使用两种描述方法：欧拉描述以及拉格朗日描述。两者都有物质导数的概念，受到时间和空间的影响。

2.1欧拉描述

  为在固定的位置取出一个控制体，只观察该控制体的流体信息变化（即控制体不动的变化）。

2.2 拉格朗日描述

为跟随流体微团进行流体信息的观察，但在CFD中用的少。

3.控制方程

可分为三大守恒方程：质量守恒、动量守恒、能量守恒方程，即控制体的质量（动量/能量）增加=穿过控制面流入的净质量（动量/能量）。如在一个空间内，一个控制体的一个小面元中有通量流过，在单位时间内流过的通量为F，则我们在计算时需要计算三个面的总和，不能漏掉任何一面。

4.流通量的计算

流通量即为流过的质量、动量、能量的总和，其详细计算过程见下图：

注：张量为一个可用来表示一些向量、标量和其他张量之间的线性关系的多线性函数，张量可以认为时标量和向量的延伸，标量为零阶张量，向量为1阶向量，也存在更高阶的张量.

5.N-S方程的无量纲化与简化

存在一个特征量，其定义为对于某物理量进行人为赋予一个值，用于实现无量纲化。无量纲量即为物理量与特征量的比值。

简化表述如下：

Ansys fluent 网格划分实例操作

在导入模型后，先进行面网格的划分，将其最模型的最小部分进行填充，以提高精度，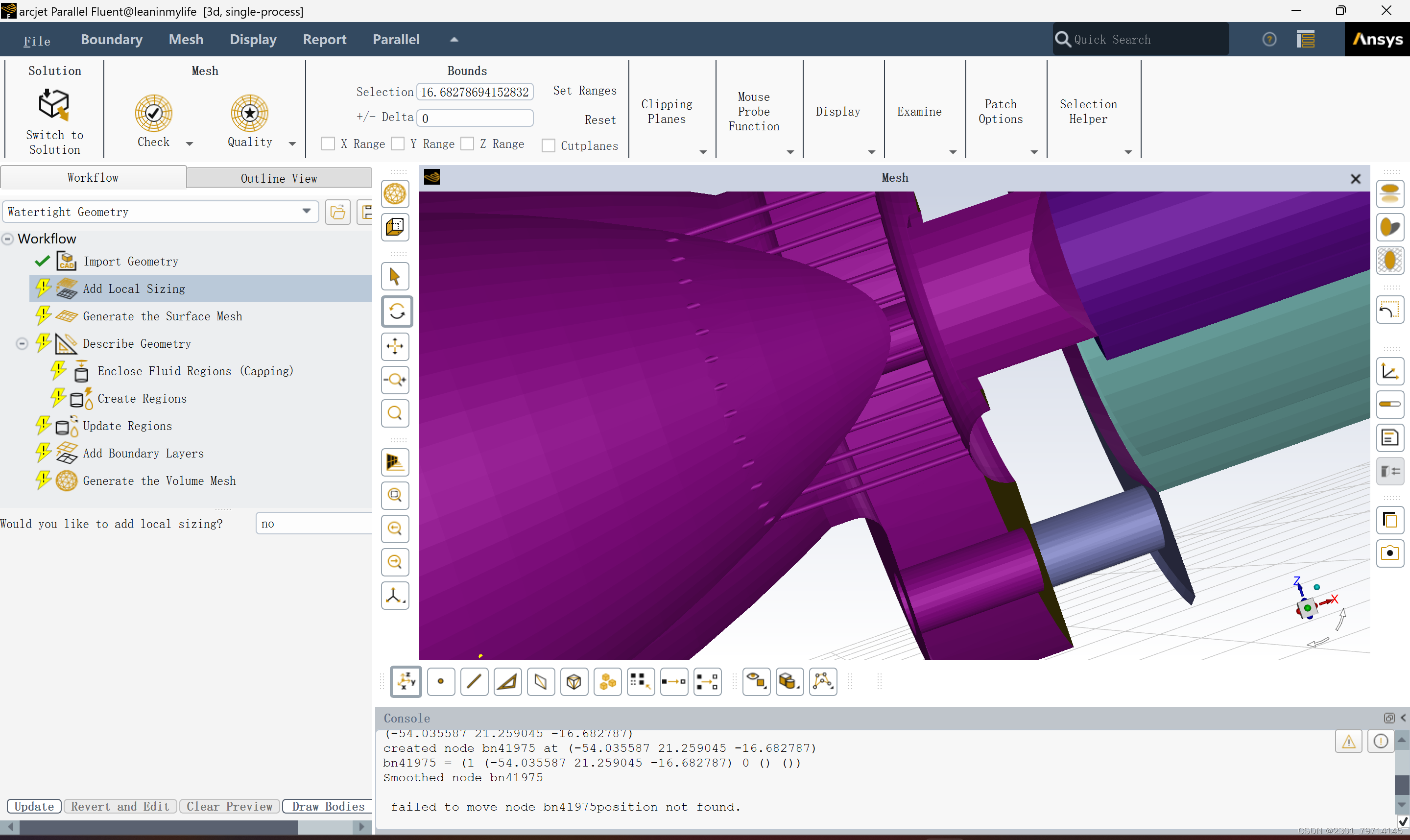

如图所示，其中小孔部分为本次模型中需要考虑的最小部分。调整精度min为0.2，使立方体能够被小孔包裹。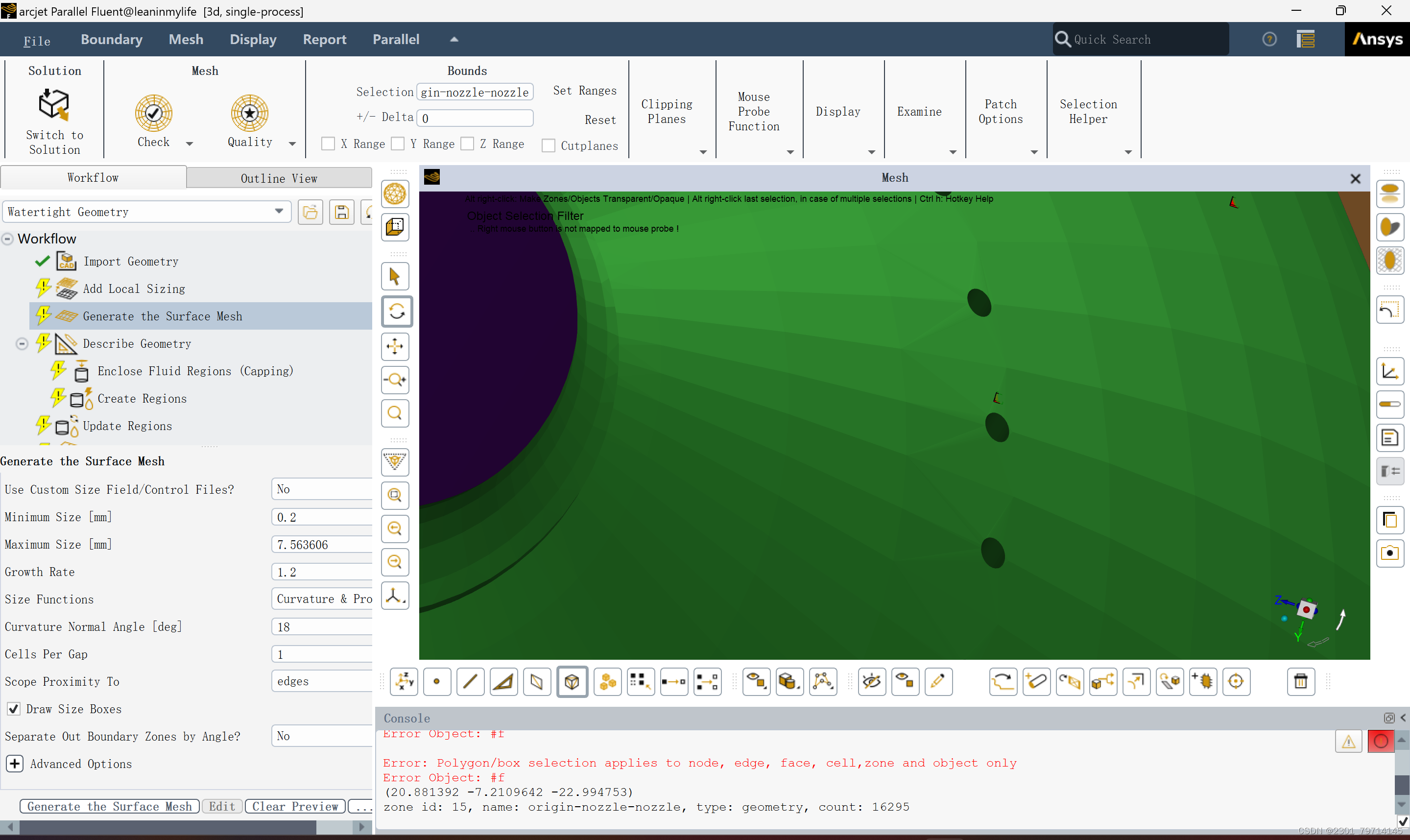

最大网格设置为5，在通常设置中，需考虑曲率、临近度等因素才能进行很好的覆盖，面网格设置最终如下所示：

最终网格划分精度约为0.68，小于0.7，符合要求，后进行出入口封口设置，将出入口命名后进行封口，保证流体流域显示正常。

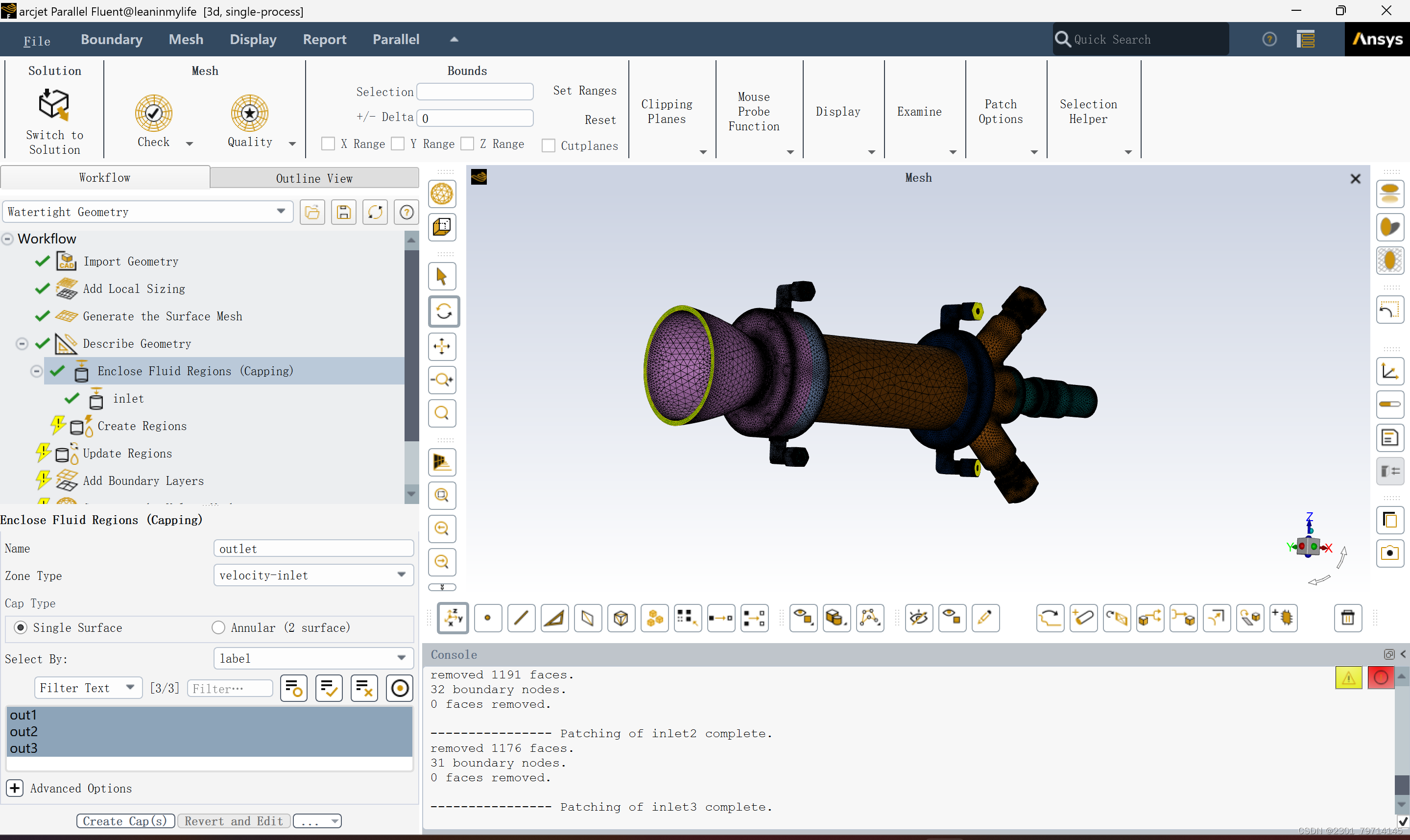
展示出流体区域，检查有无封口错误导致的流域缺失，查看后发现为两个流体域，无问题，添加边界层，便于体网格的精确分析，设置边界层为5。

后设置体网格，将网格设置为poly-hexcore多面体，尽可能减少运算量的同时又提供精度，以下为体网格划分结果：

总结

本周进行了CFD的基础理论学习以及Ansys fluent 网格划分实例操作，对于fluent，CFD是不可或缺的一门专业基础，两者息息相关，密不可分。其中偏微分方程的概念我还是觉得有些许晦涩难懂，在下周我将会着重学习了解其中的概念，学习如何使用偏微分方程来描述污染物在流场中的变化扩散情况。