【离散数学·关系】（复习）

一、

1.集合上的二元关系：

集合A上的二元关系R是A×A的子集或从A到A的关系。

2.笛卡尔积：A×B={（a,b） | 且}

问：集合A有多少种关系？ 种。（因为笛卡尔积A×A的基数为）

3.aRb表示(a,b)R。

4.other：

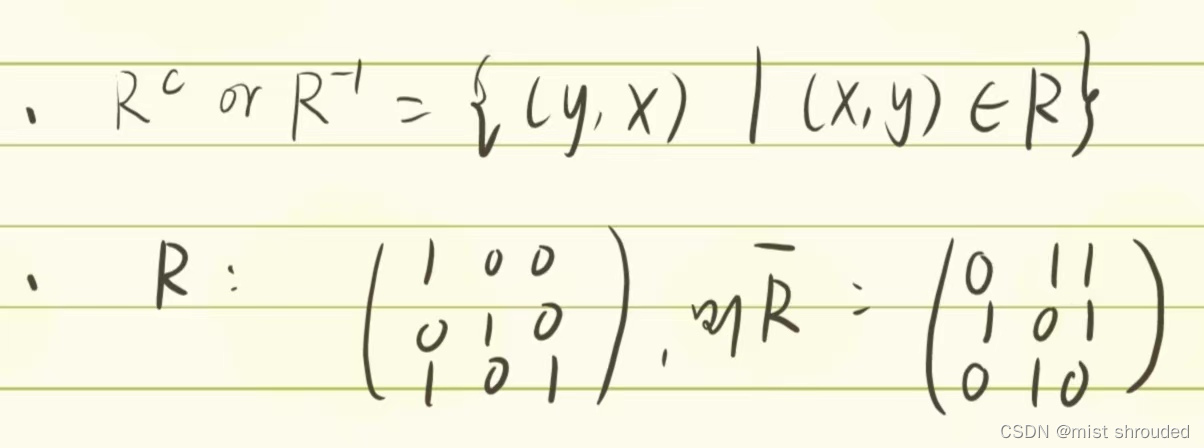
二、关系的性质

1.自反性：矩阵对角线上为1；

2.对称性：矩阵关于主对角线对称；

3.反对称性：说法（1）：对于任意的x,y，（x,y）R  （y,x）R   -> x=y;

                     说法（2）：若x!=y,(x,y)R,则一定有（y,x）R。

4.传递性：用矩阵相乘判定。（若矩阵的幂为原矩阵的子集，则有传递性）

例：

{（1，1），（2，2），（3，3），（4，4）}同时满足以上四个性质。

三、组合关系

如   等。

四、合成 (组成)

：A->B; : B->C; 则 : A->C;

五、关系的幂

，归纳：

六、关系的表示

1.用矩阵表示关系

2.用图表示关系

有向图；

a是边（a,b）的始点，b是边（a,b）的终点；

形如（a,a）的边叫做环。

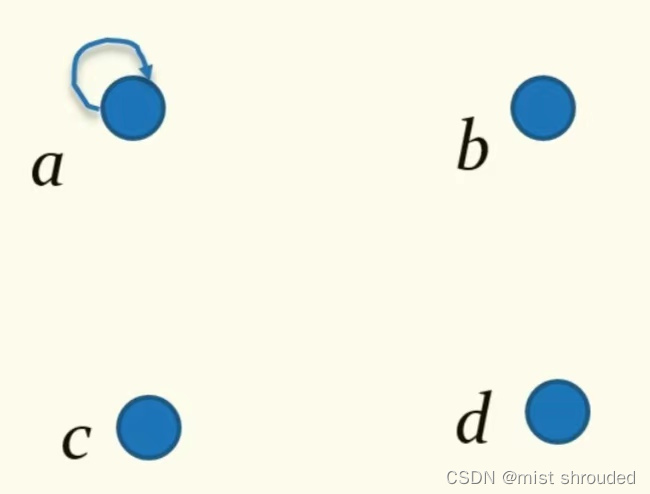   此图中，不满足自反性，满足：对称性，反对称性，传递性；

（由此图我们可以知道，对称性和反对称性可能会同时出现）

3.长度为n的路径在中；

七、等价关系

1.等价关系

（1）满足：自反，对称，传递性

（2）若a,b由于等价关系而相关联，则称它们是等价的  （ a~b）

（3）“模m同余” 是等价关系，证明：

2.等价类

设R是定义在集合A上的等价关系，与A中的一个元素a有关系的所有元素的集合叫做a的等价类。A的关于R的等价类记作；当只考虑一个关系时，写为[a]。

={s|(a,s)R};

若b,b叫这个等价类的代表元。一个等价类的任何元素都可以作为这个类的代表元。

如[1]=[4]=...={1,4,...}（模3同余）

3.等价类与划分

设R是定义在集合A上的等价关系，一下关于集合A中a、b两个元素的命题等价：

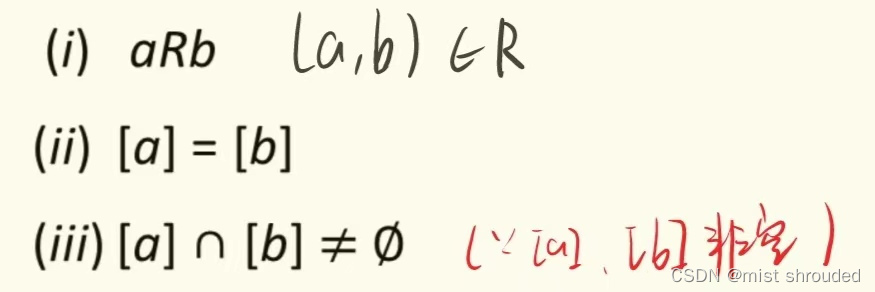
4.集合的划分  （无重复，全覆盖）

八、偏序关系

1.性质：满足自反，反对称，传递

2.记作：（S，R）  （定义在集合S上的偏序关系）

3.“整除关系” 是偏序关系  （  2|4 : 2整除4 ）

（,）是偏序集；   

九、可比性

十、哈塞（Hasse）图    （偏序）

1.构造步骤：

2.极大元，极小元：（可能是多个）

3.最大元，最小元：（可能不存在，若存在，只能是1个）

4.（1）上界：（不包括自己）

   （2）下界：（包括自己）

   （3）最小上界，最大下界；

例：

十一、字典顺序