图论进阶之二分图

冰叶日中花.acm

已于 2024-05-03 23:04:51 修改

阅读量1k

点赞数 21

文章标签：图论深度优先算法

于 2024-05-03 22:47:48 首次发布

本文链接：https://blog.csdn.net/2301_80202386/article/details/138423930

版权

二分图

文章目录

二分图

定义

$二分图，又称二部图，英文名叫 B i p a r t i t e g r a p h$

$二分图是什么？节点由两个集合组成，且两个集合内部没有边的图$

$换言之，存在一种方案，将节点划分成满足以上性质的两个集合$

在这里插入图片描述
$性质：二分图不存在奇数边的环$

$证明：因为每一条边都是从一个集合走到另一个集合，只有走偶数次才可能回到同一个集合$

$一般题型：染色法判图，最大匹配问题，最大边权匹配问题$

染色法判图

例题

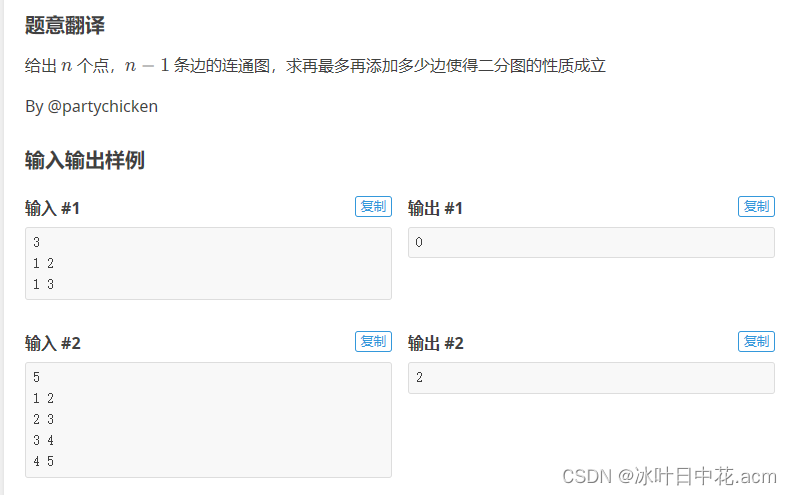
在这里插入图片描述

$染色法顾名思义就是把点染成色，由于二分图是两个集合，所以只需要两个颜色，当我们使用数组存颜色的时候$

$如果颜色用 0 和 1 来去染则不好判断该点是否被染过色，用 m e m se t 或者 a ss i g n 去初始化也有点浪费时间$

$干脆就把颜色用 1 和 2 去染，思路就打开了 : 当某一点没被染，先染成 1 ，与其连边的点就染成 2$

$到时候变色去染就可以用一个 3 - co l or 去染则方便很多, 具体的染色我们可以用 df s 或者 b f s$

$以下是这题的思路代码$

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
#define PII pair<int, int>
#define ll long long
const ll INF = 0x3f3f3f3f3f3f3f3f;

ll cnt[3];
int color[N];
vector<int>e[N];//用vector当邻接表用

void dfs(int x, int pos) {
    color[x] = pos;
    cnt[pos]++;
    for (auto &i : e[x]) {
        if (!color[i]) {
            dfs(i, 3 - pos);
        }
    }    
    return;
}

void solve() {
    int n;
    cin >> n;
    int x, y;
    for (int i = 1; i <= n - 1; i++) {
        cin >> x >> y;
        e[x].push_back(y);
        e[y].push_back(x);//注意一定是无向图
    }
    dfs(1, 1);
    cout << (cnt[1] * cnt[2] - n + 1);
    return; 
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    int T;
    //cin >> T;
    T = 1;
    while (T--) {
        solve();
    }
    return 0;
}

最大匹配问题

例题

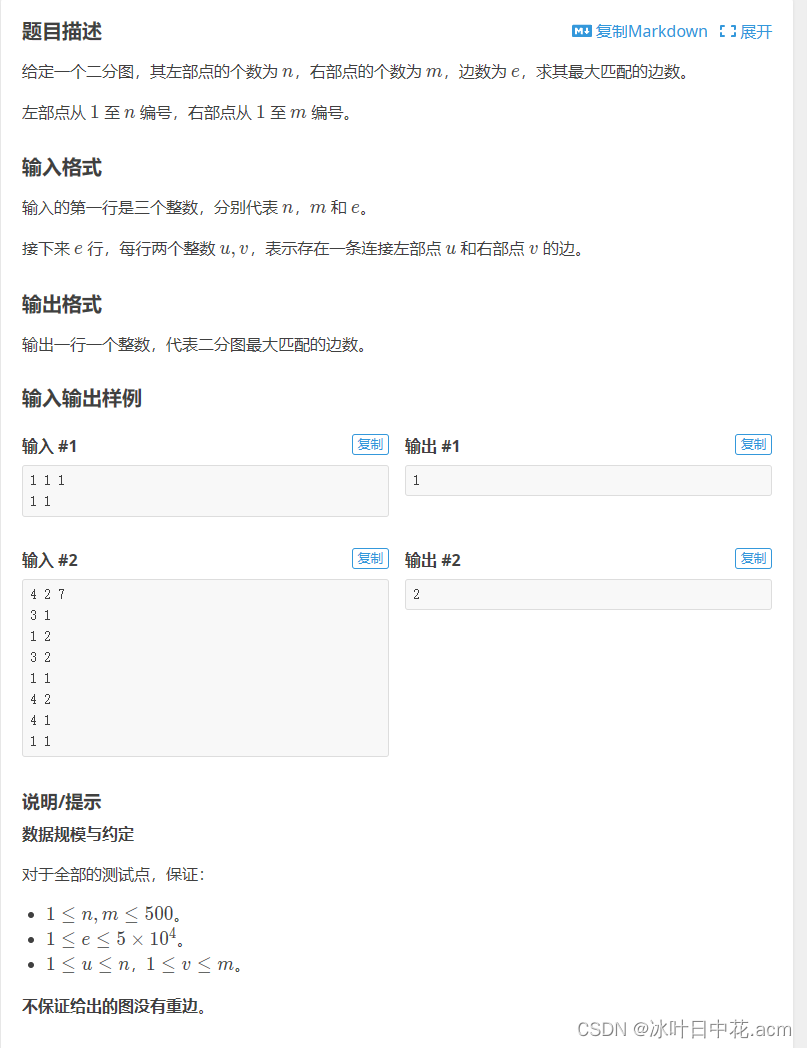
在这里插入图片描述
$二分图的最大匹配问题我们一般使用 K M (匈牙利) 算法$

$具体思路：想像成是男女配对$

在这里插入图片描述
$(t i p s : 此图与题目样例无关，只是举个例子)$

$K M 算法的思想在于一句话：待字闺中，据为己有；名花有主，求他放手$

$我们先看男 1 (从上往下标记，下同) 想与女 2 匹配，然后女 2 暂时无人与其匹配，则同意男 1$

$然后到男 2 ，男 2 与女 1 匹配，再看男 3 ，然后男 3 发现女 2 和男 1 匹配了$

$由于 K M 算法讲究一个不撞南墙不回头，所以男 3 就恳求男 1 ，让男 1 去和其他女生进行匹配$

$男 1 一看，诶，女 4 可以跟他匹配，那么男 1 和女 4 匹配，男 3 和女 2 匹配 (这就是最大匹配的精髓)$

$然后到男 4 ，男 4 和女 3 匹配，然后这个图的最大匹配数就是 4 ，各有对象$

$那么代码实现思路就出来了，每一次寻点时，用 s t 数组去判断是否匹配过， ma t c h 数组存储匹配对象$

$由于二分图只有两个集合，只需遍历其中一个集合，查询另一个集合即可$

$以下是这题的代码$

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
#define ll long long

vector<int>edge[505];
vector<int>match(505, 0);
vector<bool>st(505, false);

bool find(int x){
    for(auto &i : edge[x]){
        if(!st[i]){
            st[i] = true;
            if(!match[i] || find(match[i])){
                match[i] = x;
                return true;
            }
        }
    }
    return false;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int n, m, e;
    cin >> n >> m >> e;
    int a, b;
    while(e--){
        cin >> a >> b;
        edge[a].push_back(b); //建图建有向图
    }
    int sum = 0;
    for(int i = 1; i <= n; i++){
        st.assign(505, false);
        if(find(i))sum++;
    }
    cout << sum << "\n";
    return 0;
}

最大边权匹配问题

$这部分的内容比较难且复杂，可以做例题多体会$

$考虑到二分图中两个集合中的点并不总是相同$

$为了能应用 K M 算法解决二分图的最大权匹配，需要先作如下处理 :$

$将两个集合中点数比较少的补点，使得两边点数相同，再将不存在的边权重设为 0$

$这种情况下，问题就转换成求最大权完美匹配问题，从而能应用 K M 算法求解$

$\leq l(u) + l(v)$

$相等子图 : 在一组可行顶标下原图的生成子图，包含所有点但只包含满足 w (u, v) = l (u) + l (v) 的边 (u, v)$

$定理 1 : 对于某组可行顶标，如果其相等子图存在完美匹配，那么，该匹配就是原二分图的最大权完美匹配, 证明：$

$考虑原二分图任意一组完美匹配 M ，其边权和为$

$\sum_{(u,v)\in M} {w(u,v)} \leq \sum_{(u,v)\in M} {l(u) + l(v)} \leq \sum_{i=1}^{n} l(i)$

思路

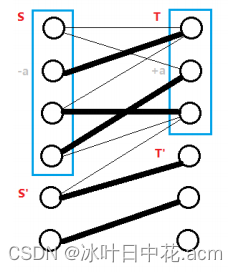
在这里插入图片描述

$任意一组可行顶标的相等子图的完美匹配 M^{'} 的边权和$

$\sum_{(u,v)\in M} {l(u) + l(v)} = \sum_{i=1}^{n} l(i)$

$即任意一组完美匹配的边权和都不会大于 v a l (M^{'}) ，那个 M^{'} 就是最大权匹配$

$有了定理 1 ，我们的目标就是透过不断的调整可行顶标，使得相等子图是完美匹配$

$因为两边点数相等，假设点数为 n ， l x (i) 表示左边第 i 个点的顶标， l y (i) 表示右边第 i 个点的顶标$

$w (u, v) 表示左边第 u 个点和右边第 v 个点之间的权重$

$首先初始化一组可行顶标，例如$

$\max_{1\leq j\leq n} \{ w(i, j)\},\, ly(i) = 0$

$然后选一个未匹配点，如同最大匹配一样求增广路。找到增广路就增广，否则，会得到一个交错树$

$令 S ， T 表示二分图左边右边在交错树中的点， S^{'} ， T^{'} 表示不在交错树中的点$

$在相等子图中：$

$S - T^{'} 的边不存在，否则交错树会增长$

$S^{'} - T 一定是非匹配边，否则他就属于 S$

$假设给 S 中的顶标 - a ，给 T 中的顶标 + a ，可以发现$

$S - T 边依然存在相等子图中$

$S^{'} - T^{'} 没变化$

$S - T^{'} 中的 l x + l y 有所减少，可能加入相等子图$

$S^{'} - T 中的 l x + l y 会增加，所以不可能加入相等子图$

$所以这个 a 值的选择，显然得是 S - T^{'} 当中最小的边权$

$\min \{ lx(u) + ly(v) - w(u,v) | u\in{S} , v\in{T'} \}$

$当一条新的边 (u, v) 加入相等子图后有两种情况$

$v 是未匹配点，则找到增广路$

$v 和 S^{'} 中的点已经匹配$

$这样至多修改 n 次顶标后，就可以找到增广路$

$每次修改顶标的时候，交错树中的边不会离开相等子图，那么我们直接维护这棵树$

$我们对 T 中的每个点 v 维护$

$\min \{ lx(u) + ly(v) - w(u,v) | u\in{S} \}$

$所以可以在 O (n) 算出顶标修改值 a$

$\min \{ slack(v) | v\in{T'} \}$

$交错树新增一个点进入 S 的时候需要 O (n) 更新 s l a c k (v) 。修改顶标需要 O (n) 给每个 s l a c k (v) 减去 a$

$只要交错树找到一个未匹配点，就找到增广路$

$一开始枚举 n 个点找增广路，为了找增广路需要延伸 n 次交错树，每次延伸需要 n 次维护，共 O(n^3)$

$若理论部分看不懂，可以结合代码思考一下$

例题

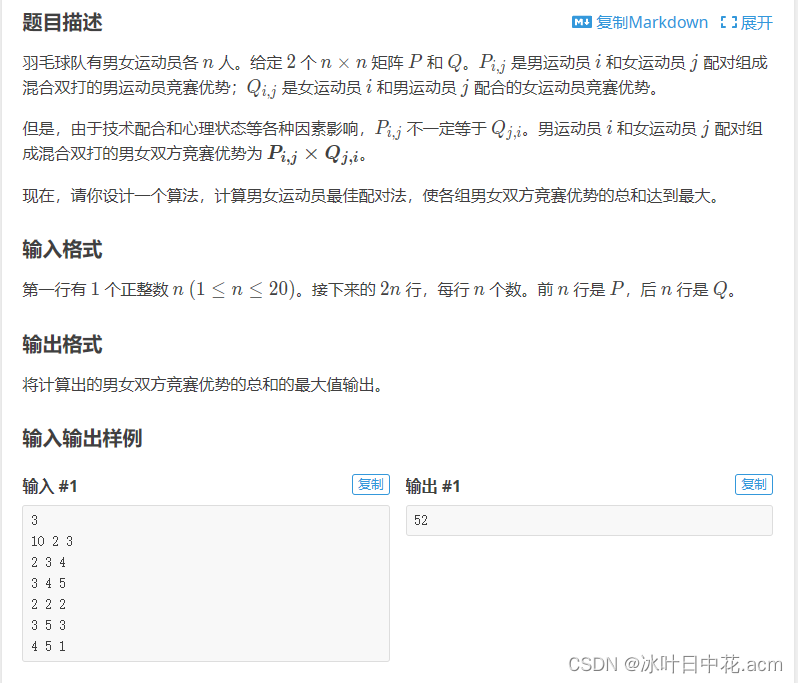
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const int N = 2e5 + 10;

vector<int>match(50), lx(50, 0), ly(50, 0);
vector<bool>sx(50), sy(50);

int a[50][50];
int n, MIN;

bool find(int x) {
    sx[x] = true;
    for (int i = 1; i <= n; i++) {
        if (!sy[i]) {
            if (lx[x] + ly[i] == a[x][i]) {
                sy[i] = true;
                if (!match[i] || find(match[i])) {
                    match[i] = x;
                    return true;
                }
            }
            else if (lx[x] + ly[i] > a[x][i]) {
                MIN = min(MIN, lx[x] + ly[i] - a[x][i]);
            }
        }
    }
    return false;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    cin >> n;
    int x;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            cin >> x;
            a[i][j] = x;
        }
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            cin >> x;
            a[j][i] *= x;
        }
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            lx[i] = max(lx[i], a[i][j]);       
        }
    }
    for (int i = 1; i <= n; i++) {
        while (1) {
            MIN = INF;
            sx.assign(25, false);
            sy.assign(25, false);
            if (find(i)) break;
            for (int j = 1; j <= n; j++) {
                if(!sx[j])continue;
                lx[j] -= MIN;
            }
            for (int j = 1; j <= n; j++) {
                if(!sy[j])continue;
                ly[j] += MIN;
            }
        }
    }
    int sum = 0;
    for (int i = 1; i <= n; i++) {
        sum += a[match[i]][i];
    }
    cout << sum << "\n";
    return 0; 
}

题单

序号	题号	标题	题型	难度评级	题解
1	Codeforces CF862B	Mahmoud and Ehab and the bipartiteness	染色法判图	⭐⭐	👍
2	luogu P1525	[NOIP2010 提高组] 关押罪犯	染色法判图	⭐⭐⭐	👍
3	luogu P1407	[国家集训队] 稳定婚姻	染色法判图	⭐⭐⭐	👍
4	luogu P3386	【模板】二分图匹配	最大匹配	⭐⭐	👍
5	luogu P2756	飞行员配对方案问题	最大匹配	⭐⭐	👍
6	luogu P1129	[ZJOI2007]矩阵游戏	最大匹配	⭐⭐⭐	👍
7	luogu P2423	[HEOI2012]朋友圈	最大匹配	⭐⭐⭐⭐⭐	👍
8	luogu P2825	[HEOI2016/TJOI2016]游戏	最大匹配	⭐⭐⭐⭐	👍
9	luogu P3033	[USACO11NOV]Cow Steeplechase	最大匹配	⭐⭐⭐⭐	👍
10	luogu P4617	[COCI2017-2018#5] Planinarenje	最大匹配	⭐⭐⭐⭐	👍
11	luogu P1559	运动员最佳匹配问题	最大边权匹配	⭐⭐⭐⭐	👍
12	luogu P4014	分配问题	最大边权匹配	⭐⭐⭐ ⭐	👍

冰叶日中花.acm

关注

21
点赞
踩
10

收藏

觉得还不错? 一键收藏
1
评论
图论进阶之二分图

二分图，又称二部图，英文名叫Bipartitegraph二分图，又称二部图，英文名叫 Bipartite graph二分图，又称二部图，英文名叫Bipartitegraph二分图是什么？节点由两个集合组成，且两个集合内部没有边的图二分图是什么？节点由两个集合组成，且两个集合内部没有边的图二分图是什么？节点由两个集合组成，且两个集合内部没有边的图换言之，存在一种方案，将节点划分成满足以上性质的两个集合。
复制链接

扫一扫