解决（使用双重逻辑符号简化）组合逻辑电路的简易方法

简介：该文章主要是关于使用“NAND（与非）”和“NOR（或非）”化简逻辑表达式以及逻辑图相关问题的另一种思路。

PS：本以为没有必要写出来，但查了相关资料，好像没有文章提及到这一点，所以写出了这片文章。

核心内容很简单，请各位多点耐心看下去。

 

一. 该文主要分“NAND”和“NOR”两种情况进行讲解。（实际原理差不多）

 

1.形如【 Y = （AB + Cfei) D + EF 的与非式，用“NAND”画出逻辑图】之类的问题。

常见方法：

①图形法：从输出端开始，奇数层  “与非”变成“非或”。

②表达式：适用于先“与”再“或”的式子，将所有“与项式”添加两次非。

具体事例如下：

 

本文推荐方法.方法二:

①：根据原逻辑表达式使用“与”门和“或”门画出逻辑表达式。

②：再根据“与非”门等同于“非或”门，将原图中的“与”→“与非”，“或”→“非或”，如下图所示。

注：此处为画图简易，将“非门”（—△o—）记作“—o—”；

未做红笔处理前的部分，为第一步操作后的逻辑图。

 ③：将“非或”换成“与非”，再根据替换后的逻辑图，写出表达式。

 

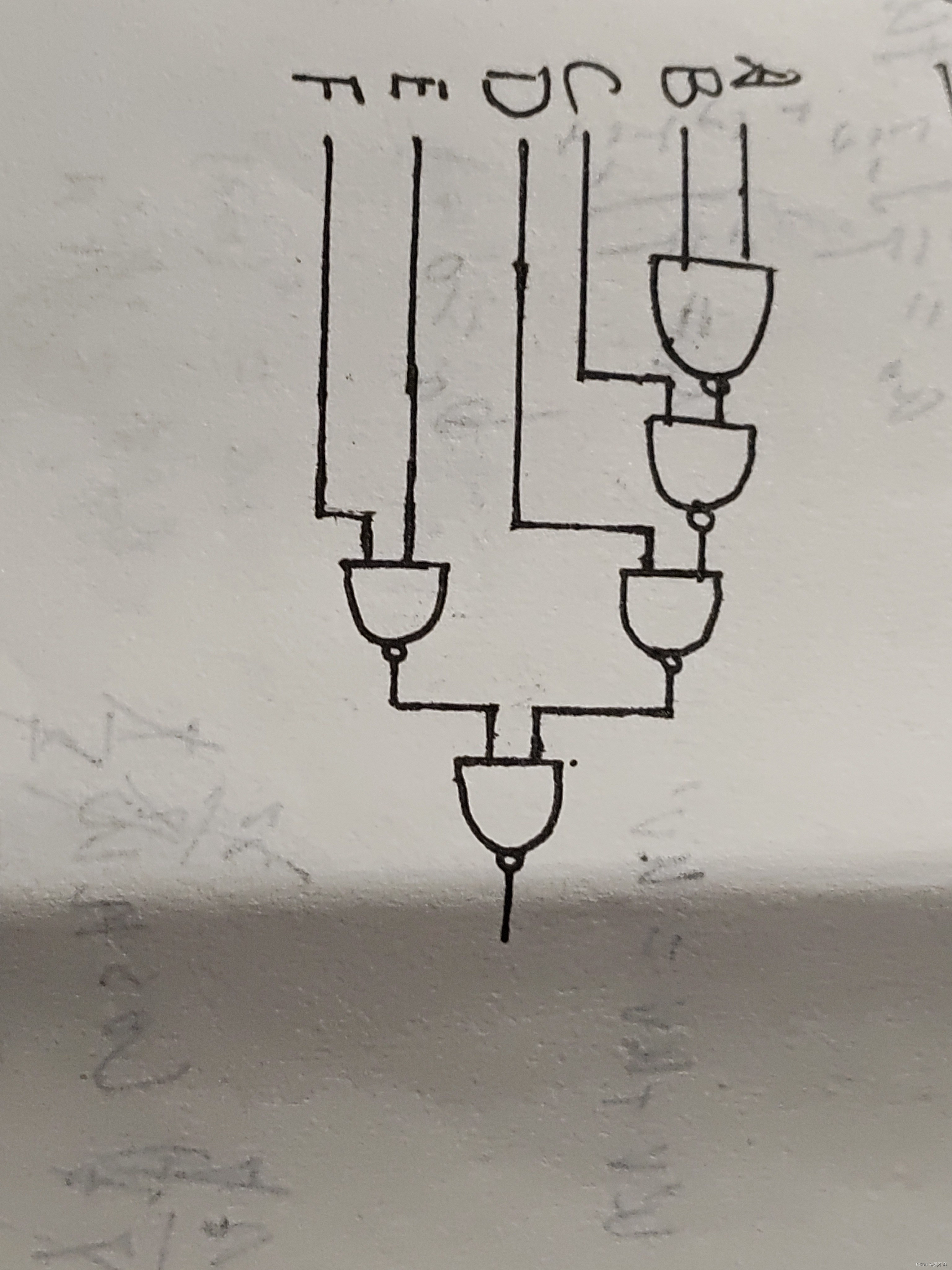
2.形如【 Y = [（A+B)C fei + D ](E+F) 的或非式，用“NOR”画出逻辑图】之类的问题。

常见方法：

①图形法：从输出端开始，奇数层  “或非”变成“非与”。

 

②表达式：适用于先“或”再“与”的式子，将所有“或项式”添加两次非。

 

具体事例如下：

 

本文推荐方法.方法二:

①：根据原逻辑表达式使用“与”门和“或”门画出逻辑表达式。

②：再根据“或非”门等同于“非与”门，将原图中的“或”→“或非”，“与”→“非与”，如下图所示。

注：此处为画图简易，将“非门”（—△o—）记作“—o—”；

未做红笔处理前的部分，为第一步操作后的逻辑图。

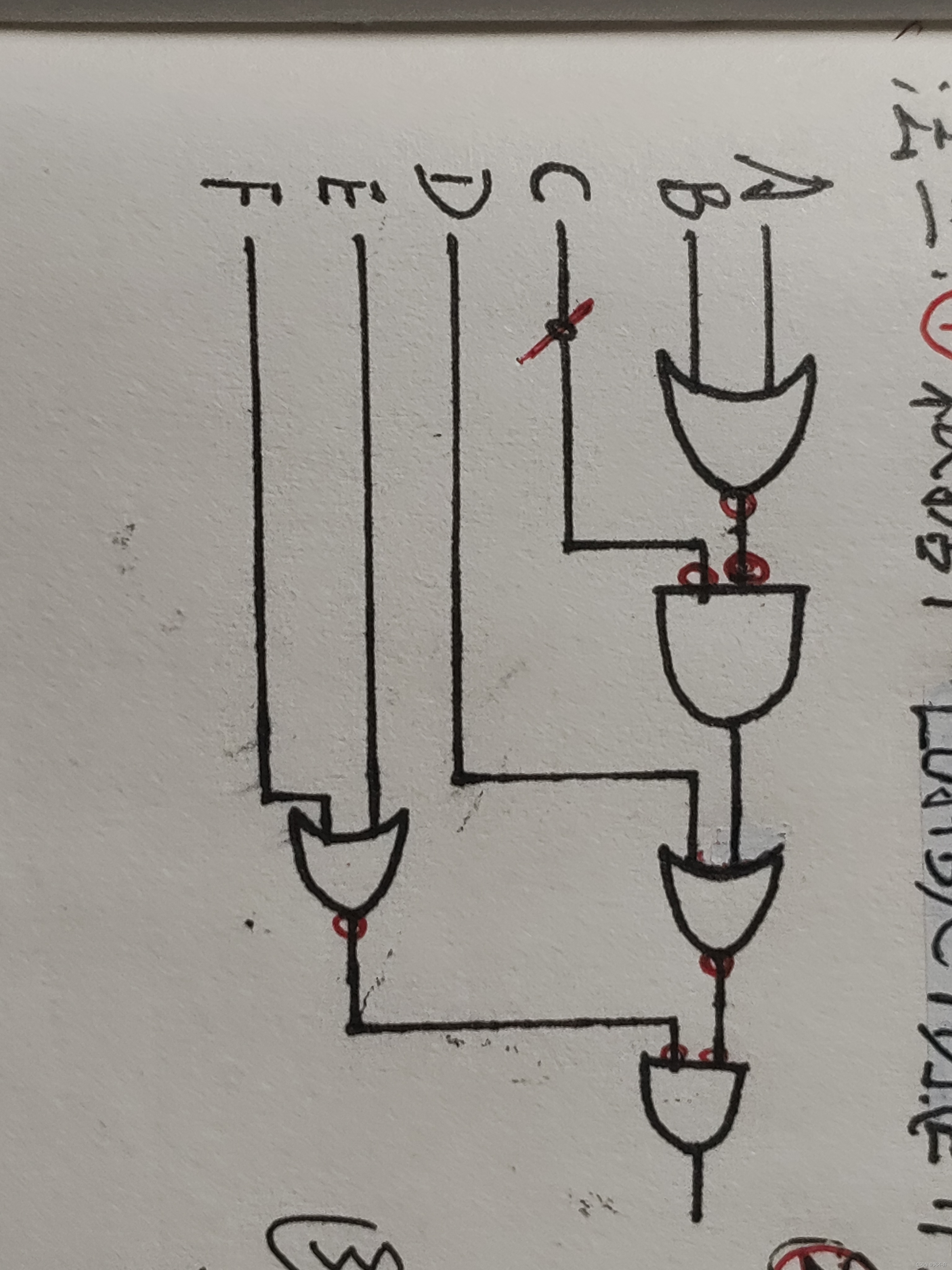
 ③：将“非与”换成“或非”，再根据替换后的逻辑图，写出表达式。

 

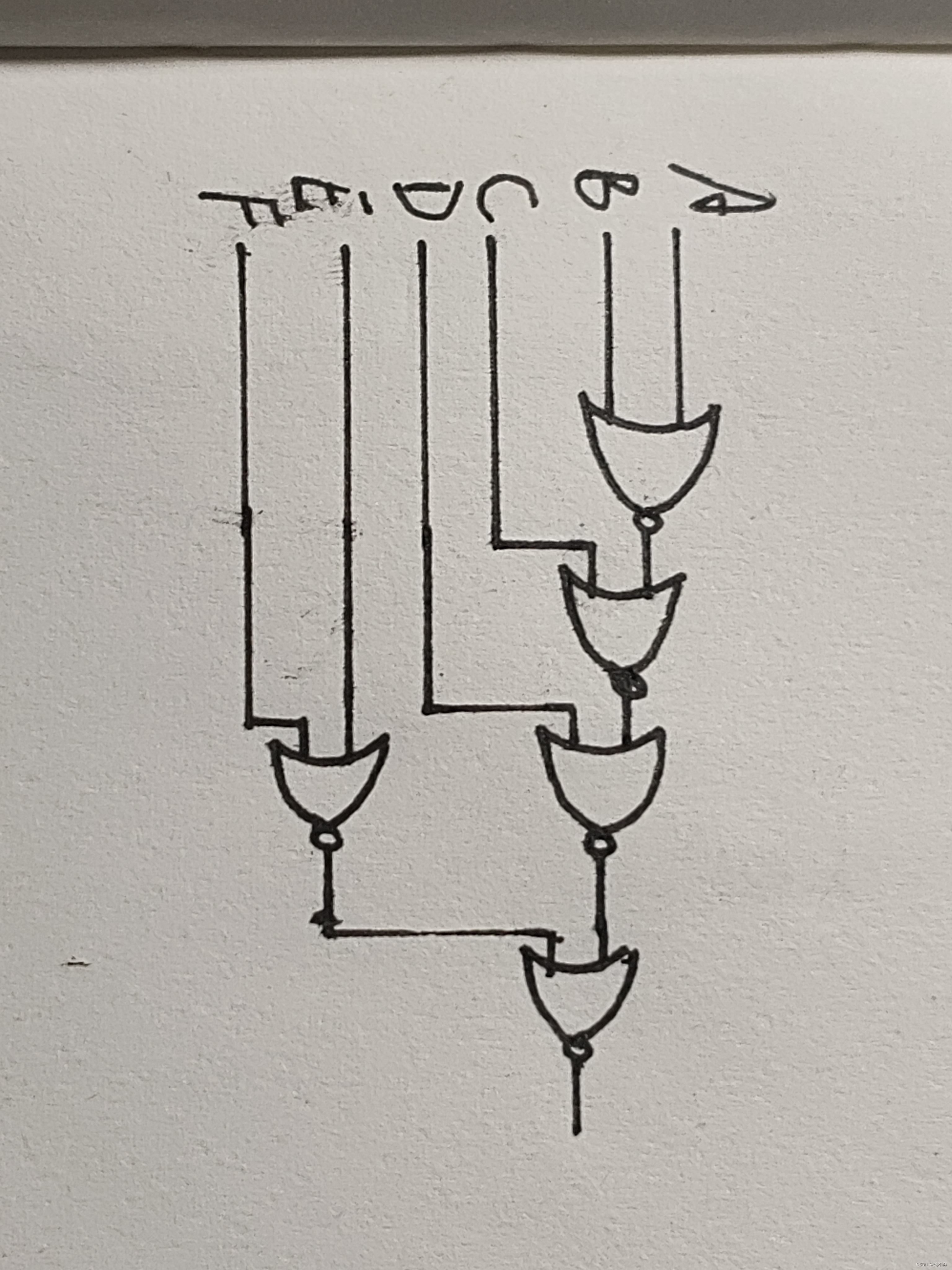
 总结：

①先根据原逻辑表达式用“与”门和“或”门画出逻辑图。

②在根据类型如：“NAND”就将“与”→“与非”，“或”→“非或”。

注意，其根本原理在于两个非门相互抵消，不要盲目的变换。

③再根据要求，统一逻辑符号。

 

希望本章对你有所帮助，期待下一次相遇。