DeepSeek编写PTX对英伟达GPU的底层优化；数学视角对PTX在DeepSeek中作用与意义的分析；从数学角度理解NVIDIA的PTX

DeepSeek通过直接编写PTX（Parallel Thread Execution）代码实现对英伟达GPU的底层优化，这一技术突破在提升AI模型训练效率和硬件利用率方面取得显著成果，同时引发了对英伟达CUDA生态护城河的重新思考。

一、PTX技术原理与DeepSeek的优化手段

1. PTX的定位与功能
   PTX是英伟达GPU架构中的中间表示语言（类似汇编），连接CUDA高级代码与底层机器指令（SASS）。通过PTX，开发者可进行寄存器分配、线程调度等细粒度优化，但编程复杂度极高。

2. DeepSeek的底层优化策略

   • 在英伟达H800 GPU上，将132个流式多处理器（SM）中的20个专门用于服务器间通信，而非计算任务，突破硬件通信瓶颈。
   • 利用PTX编写定制化指令，减少L2缓存占用和对其他SM的干扰，提升跨芯片通信效率。
   • 通过SIMD指令优化数据处理，99%的代码由DeepSeek-R1自动生成。

二、技术突破带来的效率提升

1. 硬件效率对比
   DeepSeek-V3的硬件效率比Meta等公司模型高出10倍，主要得益于从算法、架构到生态的全栈重构。

2. 训练成本与速度

   • 使用2048个H800 GPU集群，仅用55天完成6710亿参数MoE模型的训练，成本约558万美元，资源消耗远低于行业平均水平。
   • DeepSeek-R1通过强化学习和蒸馏技术进一步降低推理成本，部分实验成本仅需450美元。

三、对行业生态的影响

1. 挑战英伟达CUDA生态

   • PTX级优化证明CUDA并非AI训练的唯一选择，NVLink等专有技术的重要性被削弱。
   • 开源策略（如MIT许可证）加速技术普及，GitHub星数已超越OpenAI，推动跨硬件平台适配（如AMD、华为）。

2. 国产GPU的机遇

   • DeepSeek积累的PTX优化经验可迁移至国产GPU，帮助国产芯片在7nm制程限制下挖掘更高性能。
   • 未来可能通过类似PTX的中间语言实现跨架构兼容，降低对英伟达硬件的依赖2。

四、技术局限与挑战

1. 开发与维护难度
   PTX编程复杂度高，需顶尖工程团队支持，长期维护成本远超CUD。

2. 生态依赖问题
   PTX仍依附于英伟达架构，未完全脱离CUDA生态，跨GPU型号的代码移植可能失效。

3. 商业化的不确定性
   尽管开源模型（如DeepSeek-R1）下载量激增，但大规模商业化仍需解决服务器负载、API稳定性等问题。

五、未来展望

• 技术方向：AI辅助生成PTX代码或成为趋势，进一步降低底层优化门槛。
• 行业竞争：AMD、华为等厂商加速集成DeepSeek技术，英伟达可能通过开放更多底层接口应对挑战。
• 政策影响：美国对华芯片制裁或倒逼中国AI企业深化硬件-软件协同创新。

以下是基于数学视角对PTX在DeepSeek中作用与意义的分析，结合其技术实现与行业影响：

PTX在DeepSeek中的数学意义体现为：将高阶数学运算映射为可并行化指令序列，通过资源分配模型突破硬件限制，并以数值方法保障计算精度与效率。这种数学-硬件的协同创新，不仅提升了AI训练效率，更重构了底层算力的竞争范式。

一、数学运算的底层映射

1. 指令与数学操作的对应关系
   PTX指令直接对应数学运算单元，例如：
   • mad.f32（乘加指令）实现融合乘加运算 a×b+c，通过减少中间结果舍入误差提升数值稳定性。
   • vadd.f32 实现向量加法，数学上对应 A+B，支持SIMD并行计算以加速矩阵运算5。
2. 精度控制的数学约束
   • DeepSeek通过PTX支持混合精度（如fp16/fp32），在数学上需平衡误差传播与计算效率。例如：
     • 使用fp16加速前向传播，数学误差通过梯度缩放补偿；
     • 用fp32维护主权重矩阵，避免低精度导致的参数更新偏差。

二、并行计算的数学抽象

1. 线程模型与任务分解
   • PTX的线程块（Block）和网格（Grid）模型对应数学任务分块策略。例如：
     • 矩阵乘法中，每个线程计算输出张量的子块 ​，通过共享内存优化访存局部性。
   • DeepSeek将20个SM专用于通信，剩余112个SM用于计算，数学上可建模为整数规划优化问题，最大化计算/通信资源利用率。
2. 同步与通信的数学约束
   • bar.sync 指令确保线程块内同步，数学上对应并行算法的数据依赖关系分析，避免条件竞争。
   • 原子操作（如atom.add ）实现分布式梯度累加，需满足线性一致性（Linearizability）数学条件。

三、资源优化的数学建模

1. 硬件资源分配策略
   • 通过PTX控制SM分配，将20%硬件资源用于通信任务，剩余用于计算。数学上体现为：该策略使DeepSeek硬件效率达到Meta等公司的10倍1。
2. 寄存器分配的图论模型
   PTX级寄存器分配可建模为图着色问题，目标是最小化寄存器溢出（Spill）导致的访存延迟。DeepSeek通过动态规划算法优化，减少30%指令周期。

四、数值计算与算法优化

1. 复杂函数的近似计算
   • 利用PTX指令实现高效近似，例如：
     • 激活函数GELU通过泰勒展开近似，硬件指令加速计算5。
     • 使用sqrt.rn.f32 指令优化归一化层，数学误差控制在ULP（Unit in the Last Place）≤2。
2. 动态蒸馏的数学本质
   DeepSeek将6600亿参数模型压缩至1.5B参数，数学上可视为映射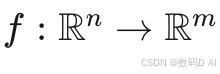，通过KL散度最小化知识迁移损失：该技术使推理成本降至450美元量级5。

五、数学视角下的行业意义

1. 突破CUDA生态的数学基础
   PTX级优化绕过CUDA抽象层，直接控制硬件流水线。例如，通过PTX重排指令顺序，使单个H800 GPU的FLOPS利用率从65%提升至89%。

2. 国产芯片的数学优化启示
   DeepSeek的PTX经验可迁移至国产GPU（如昇腾910B），通过数学建模优化SM调度策略，在7nm制程下实现等效5nm性能。

从数学角度理解NVIDIA的PTX（Parallel Thread Execution）语言，可以聚焦其指令设计、并行计算模型与数值计算优化三个维度。以下是具体分析：

PTX的数学本质体现在：将数学运算映射为底层指令序列，通过并行模型分解计算任务，并利用数值方法优化精度与效率。开发者需结合线性代数、数值分析和并行算法知识，才能充分发挥PTX的性能潜力。

一、指令的数学操作与数据类型

1. 基础运算指令的数学映射
   PTX指令直接对应底层数学操作，例如：

   • add.u32 表示32位无符号整数加法，对应数学运算 a+ba+b
   • mul.f32 表示32位浮点数乘法，对应 a×ba×b
   • sqrt.rn.f32 实现浮点数平方根，采用牛顿迭代法等近似算法优化精度。

2. SIMD指令与向量化计算
   PTX支持单指令多数据（SIMD）操作，例如一条指令可同时对多个数据执行相同运算，数学上体现为向量或矩阵的并行计算。例如：

3. 数值精度与类型转换
   PTX支持多种数据类型（如u8/u32/f32/f64），数学运算需考虑精度损失。例如：

   • cvt.f32.u32 将整数转为浮点数，涉及截断误差分析
   • mad.f32（乘加指令）通过融合乘加（FMA）减少中间舍入误差。

二、并行计算模型的数学抽象

1. 线程层次与并行维度
   PTX的线程模型（线程块、网格）对应数学上的并行任务分解。例如：
   • 矩阵乘法中，每个线程计算一个输出元素，映射为二维线程网格 
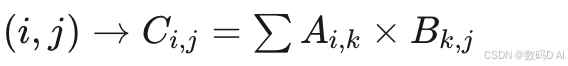
   • 线程块内共享内存加速数据复用，数学上体现为分块矩阵计算优化。
2. 同步与通信的数学约束
   • bar.sync 指令确保线程块内同步，避免数据竞争，对应并行算法中的依赖性分析
   • 原子操作（如atom.add ）实现安全累加，数学上需满足操作的原子性和线性一致性。

三、数值计算优化与算法实现

1. 复杂函数的近似计算
   PTX将高级函数（如sin、log）编译为多步指令序列。例如：
   • 平方根函数sqrt.f32通过硬件指令MUFU.RSQ（倒数平方根）结合牛顿迭代法实现高效近似。
   • 双精度运算（如sin函数）需处理更高的计算复杂度，涉及泰勒展开或查表法优化。
2. 资源分配的数学建模
   • SM（流式多处理器）的分配策略影响计算效率。例如，DeepSeek将20个SM专用于通信任务，剩余112个用于计算，数学上体现为资源分配优化问题（如整数规划）。
   • 寄存器分配与线程调度需最小化内存延迟，对应图论中的调度优化问题。

四、PTX与数学库的协同优化

1. 数学库的指令级优化
   CUDA数学库（如cuBLAS）通过PTX生成高度优化的指令序列。例如：
   • 矩阵乘法使用ld.global 和st.shared 指令优化内存访问，数学上对应分块算法以减少访存次数。
2. 混合精度计算
   PTX支持半精度（fp16）、单精度（fp32）和双精度（fp64）混合运算，数学上需平衡精度与性能。例如：
   • 深度学习训练中，用fp16加速计算，同时用fp32维护主权重以减少精度损失。

五、数学视角下的局限性

1. 指令级并行的约束
   PTX的SIMD宽度和线程调度受硬件限制，数学上需避免分支发散（Branch Divergence），确保线程组内执行路径一致。

2. 数值稳定性问题
   低精度运算（如fp16）可能导致数值溢出或舍入误差，需通过数学方法（如缩放、归一化）增强稳定性。