深入解析交换排序：从基础到优化的全面解析-CSDN博客

本文链接：https://blog.csdn.net/2301_82213854/article/details/142909786

😎在之前文章中我们学习过了多种排序算法，现在我们来学习排序算法中的交换排序。

👉【选择排序】

👉【插入排序】

💯引言

交换排序作为一类重要的排序算法，以其独特的思想和实现方式在众多算法中占据一席之地。

😁本文将对交换排序进行深度解析，包括其基本原理、常见算法（冒泡排序和快速排序）的详细分析、时间复杂度与空间复杂度的探讨，以及实际应用场景和性能优化策略等方面。

💯交换排序的基本原理

交换排序的核心思想是通过不断交换元素的位置，使得序列中的元素逐渐有序。它基于比较两个元素的大小关系，若不满足既定的顺序要求，则交换它们的位置。这种反复比较和交换的操作持续进行，直到整个序列达到有序状态。

👇动图图解：

💯常见的交换排序算法

⭐冒泡排序

1.算法描述

冒泡排序是一种最简单的交换排序算法。它重复地走访要排序的数列，一次比较两个相邻的元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。

😐具体步骤如下：

比较相邻的元素。如果第一个比第二个大，就交换它们两个。
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

👇图解分析：

✍我们以一个未排序的数组为例：

冒泡排序从最初的两个元素开始，比较它们以检查哪个更大。

在这种情况下，值 33 大于 14，所以它已经在排序的位置。接下来，我们比较 33 和 27。

我们发现 27 比 33 小，这两个值必须交换。

接下来我们比较 33 和 35。我们发现它们已经处于排序的位置。

然后我们移动到下两个值，35 和 10。

我们知道 10 比 35 小。因此它们没有排序。我们交换这些值。我们发现我们已经到达了数组的末尾。经过一次迭代，数组应该如下所示：

确切地说，我们现在展示每次迭代后数组应该是什么样子。经过第二次迭代，它应该如下所示：

注意，每次迭代后，至少有一个值移动到末尾。

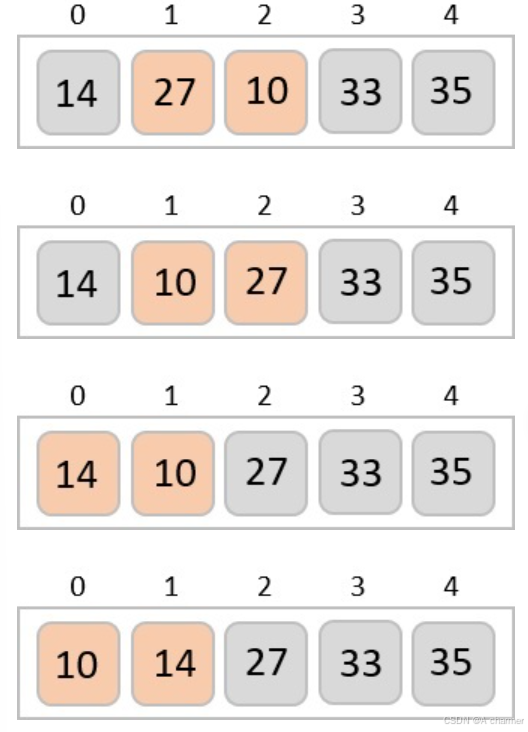
当不需要交换时，冒泡排序知道数组已完全排序。

2.示例代码（C++ 实现）

   #include <iostream>
   #include <vector>

   using namespace std;

   vector<int> bubbleSort(vector<int> arr) {
       int n = arr.size();
       for (int i = 0; i < n; i++) {
           bool swapped = false;
           for (int j = 0; j < n - i - 1; j++) {
               if (arr[j] > arr[j + 1]) {
                   swap(arr[j], arr[j + 1]);
                   swapped = true;
               }
           }
           if (!swapped) break;
       }
       return arr;
   }

3.时间复杂度分析

最坏情况：当序列是逆序时，需要进行的比较和交换次数最多。对于长度为 $n$ 的序列，第一轮需要比较 $n-1$ 次，第二轮需要比较 $n-2$ 次，以此类推，最后一轮需要比较 $1$ 次。所以总的比较次数为 $sum_{i = 1}^{n - 1}i=\frac{n(n - 1)}{2}$ ，其时间复杂度为 $O(n^2)$ 。
最好情况：当序列已经是有序时，只需要进行 $n-1$ 次比较，无需交换，时间复杂度为 $O(n)$
平均情况：平均情况下，时间复杂度也为 $O(n^2)$

4.空间复杂度分析

冒泡排序只需要在交换元素时使用一个额外的临时变量，因此空间复杂度为 $O(1)$ ，它是一种原地排序算法。

⭐快速排序

1.算法描述

快速排序是一种高效的排序算法，采用分治的思想。👀它首先选取一个基准元素（pivot），将数列分成两部分，使得左边部分的所有元素都小于等于基准元素，右边部分的所有元素都大于等于基准元素。然后分别对这两部分递归地进行快速排序。
😬以下动画表示解释了如何在数组中找到基准元素（pivot）:枢轴值将列表划分为两部分。然后递归地，我们为每个子列表找到枢轴，直到所有列表只包含一个元素。

😕具体步骤如下：

从数列中选取一个基准元素。
重新排序数列，将所有小于基准元素的元素放在基准元素的左边，将所有大于基准元素的元素放在基准元素的右边（相同大小的元素可以放在任意一边）。在这个分区过程中，基准元素的位置会被确定下来。
对基准元素左边和右边的子数列分别递归地执行上述两个步骤，直到整个数列有序。

2.示例代码（C++ 实现）

   #include <iostream>
   #include <vector>

   using namespace std;

   int partition(vector<int>& arr, int low, int high) {
       int pivot = arr[high];
       int i = low - 1;
       for (int j = low; j < high; j++) {
           if (arr[j] < pivot) {
               i++;
               swap(arr[i], arr[j]);
           }
       }
       swap(arr[i + 1], arr[high]);
       return i + 1;
   }

   void quickSort(vector<int>& arr, int low, int high) {
       if (low < high) {
           int pivotIndex = partition(arr, low, high);
           quickSort(arr, low, pivotIndex - 1);
           quickSort(arr, pivotIndex + 1, high);
       }
   }

3.时间复杂度分析

最坏情况：当每次划分选取的基准元素都是当前子序列中的最大或最小元素时，划分得到的两个子序列一个为空，另一个子序列的长度为 $n-1$ 。此时，快速排序退化为冒泡排序，时间复杂度为 $O(n^2)$ 。
最好情况：每次划分都能将序列均匀地分成两个子序列，此时时间复杂度为 $O(nlogn)$ 。
平均情况：快速排序的平均时间复杂度为 $O(nlogn)$ 。

4.空间复杂度分析

快速排序的空间复杂度主要取决于递归调用的栈空间。在最好情况下，递归树的深度为 $logn$ ，空间复杂度为 $O(logn)$ ；在最坏情况下，递归树的深度为 $n$ ，空间复杂度为 $O(n)$ 。平均情况下，空间复杂度为 $O(logn)$ 。

💯交换排序的性能优化策略

⭐冒泡排序的优化

1.设置标志位

在冒泡排序的每一轮遍历中，如果没有发生元素的交换，说明序列已经有序，可以提前结束排序。通过设置一个标志位来记录是否发生了交换操作，例如：

   vector<int> bubbleSortOptimized(vector<int> arr) {
       int n = arr.size();
       for (int i = 0; i < n; i++) {
           bool swapped = false;
           for (int j = 0; j < n - i - 1; j++) {
               if (arr[j] > arr[j + 1]) {
                   swap(arr[j], arr[j + 1]);
                   swapped = true;
               }
           }
           if (!swapped) break;
       }
       return arr;
   }

2.选择合适的步长

对于某些特殊的数据分布，可以采用不同的步长进行比较和交换。例如，在处理间隔较大的逆序对时，可以先以较大的步长进行初步的排序，然后逐渐减小步长，进行更精细的排序。这种策略类似于希尔排序的思想，但在冒泡排序中可以根据具体数据情况适当调整步长，以提高效率。

⭐快速排序的优化

1.合理选择基准元素

选择合适的基准元素可以改善快速排序的性能。一种常见的方法是选择序列的中间元素、首元素和尾元素的中位数作为基准元素，这样可以减少在极端情况下（如序列已经有序或逆序）的性能退化。例如：

   int medianOfThree(vector<int>& arr, int low, int high) {
       int mid = (low + high) / 2;
       if (arr[low] > arr[mid])
           swap(arr[low], arr[mid]);
       if (arr[low] > arr[high])
           swap(arr[low], arr[high]);
       if (arr[mid] > arr[high])
           swap(arr[mid], arr[high]);
       return arr[mid];
   }

   void quickSortOptimized(vector<int>& arr, int low, int high) {
       if (low < high) {
           int pivot = medianOfThree(arr, low, high);
           int pivotIndex = partition(arr, low, high, pivot);
           quickSortOptimized(arr, low, pivotIndex - 1);
           quickSortOptimized(arr, pivotIndex + 1, high);
       }
   }

2.减少不必要的交换

在快速排序的划分过程中，可以通过一种更巧妙的方式来移动元素，减少不必要的交换操作。例如，使用双指针法，一个指针从左向右扫描找到大于基准元素的位置，另一个指针从右向左扫描找到小于基准元素的位置，然后交换这两个位置的元素，直到两个指针相遇。这样可以在不影响排序正确性的前提下，提高算法的效率。