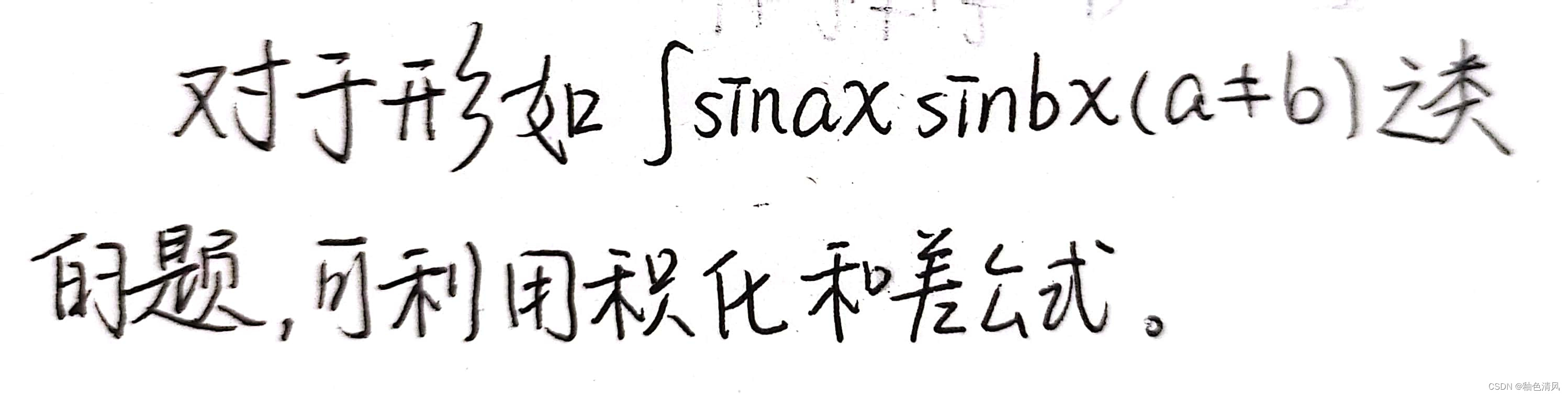
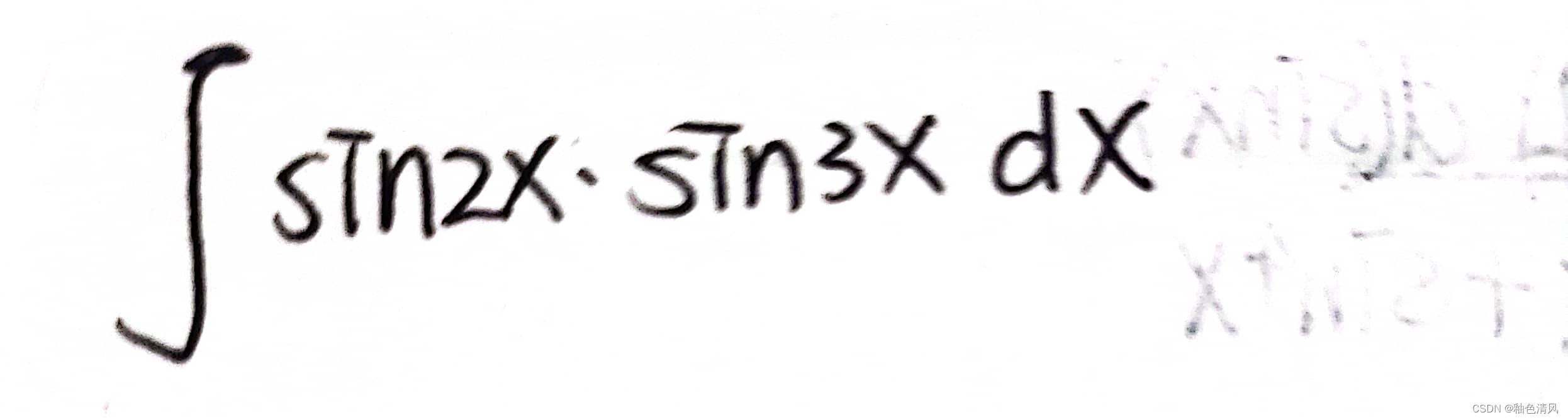
积化和差,可以直接凑。想一下什么展开会有sin ×sin,cos(x+y)和cos(x-y)可以!
所以cos(2x+3x)和cos(2x-3x),为了消去cos这一项,所以这两项相减。
过程:
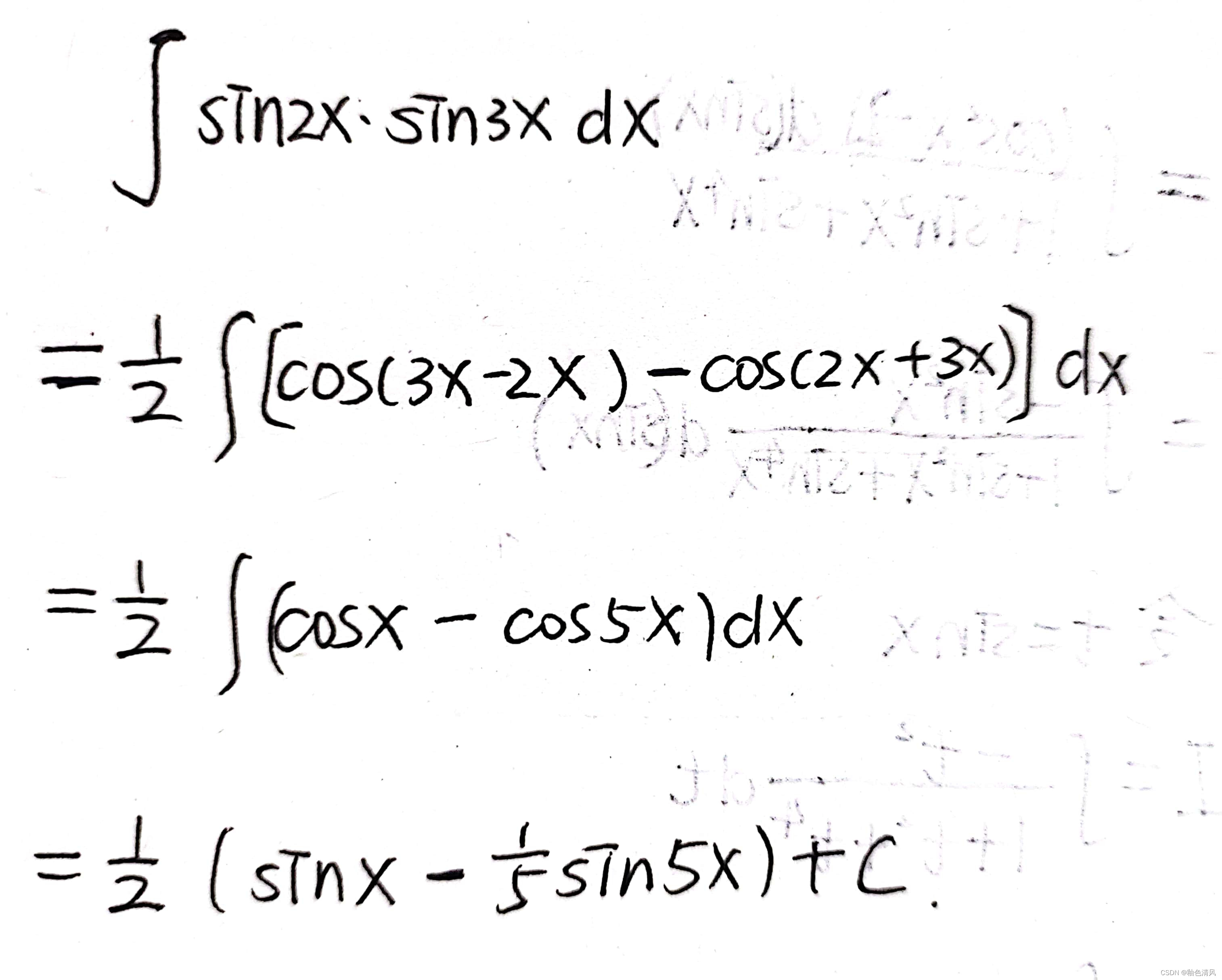
类题1
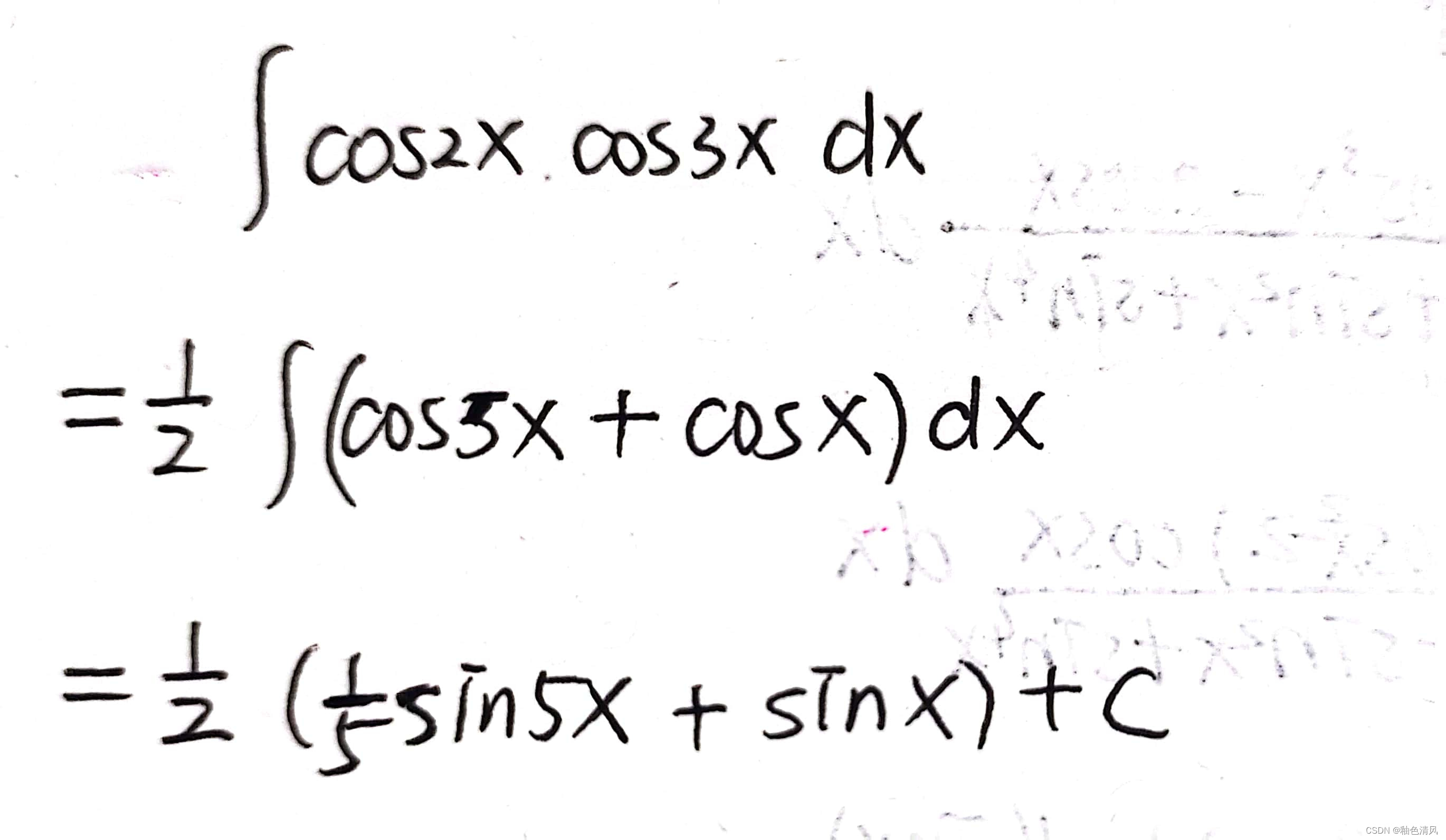
类题2
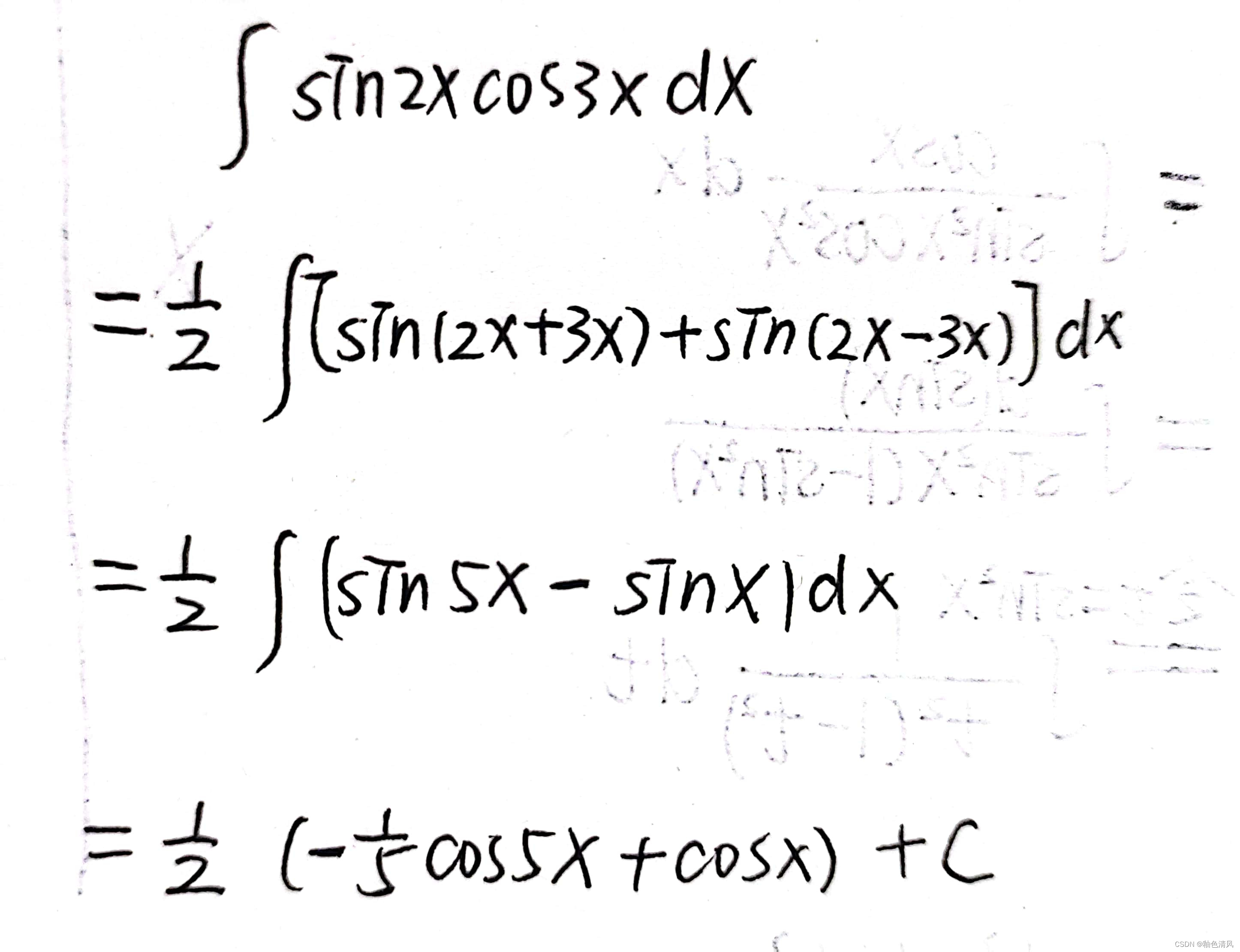
三角函数不定积分常用方法及相应类题差不多都已经补充完了。下面👇来展现几道还不错的例题。
例题(1)
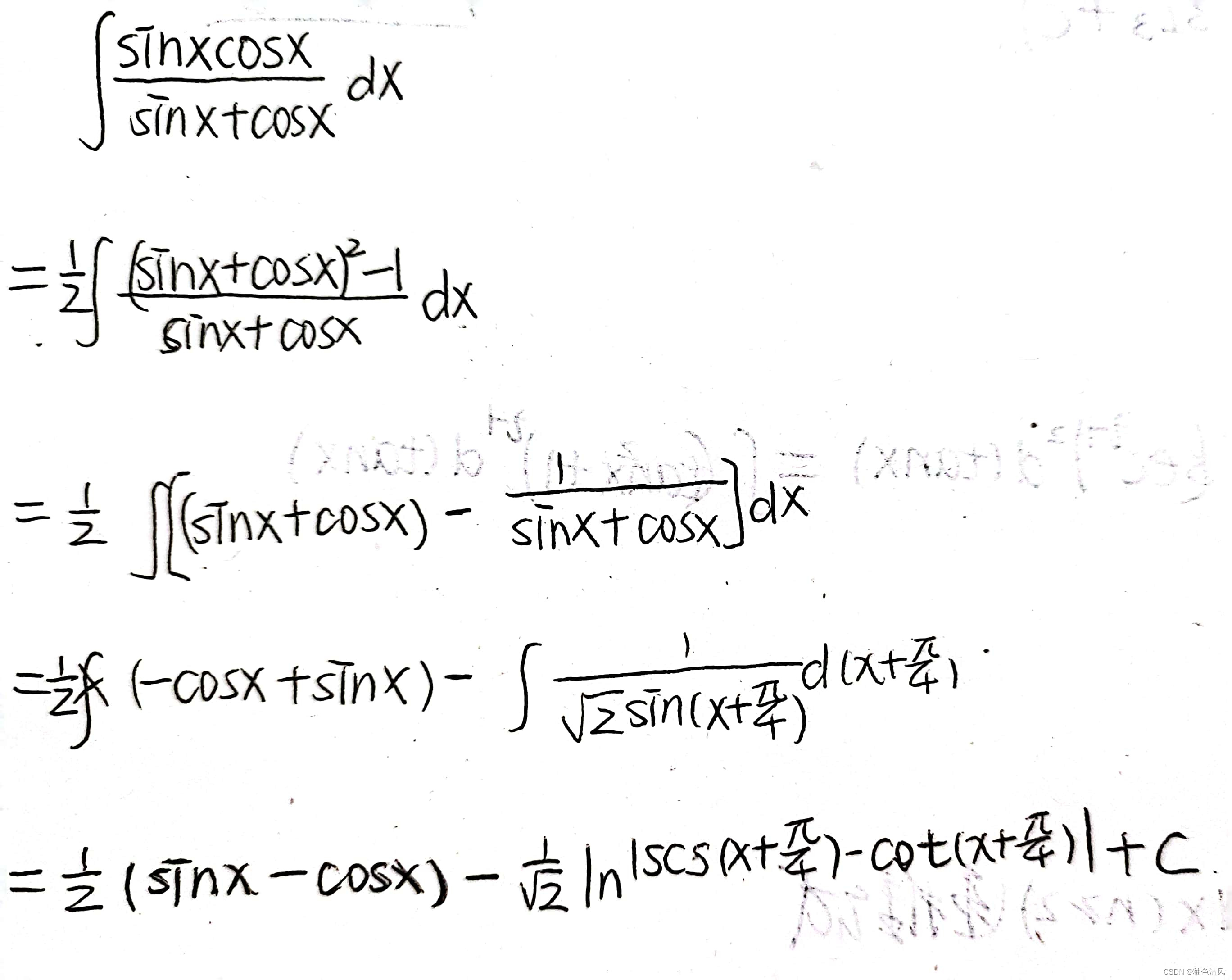
之前已经总结了,主要利用三角函数的恒等变换。
类题
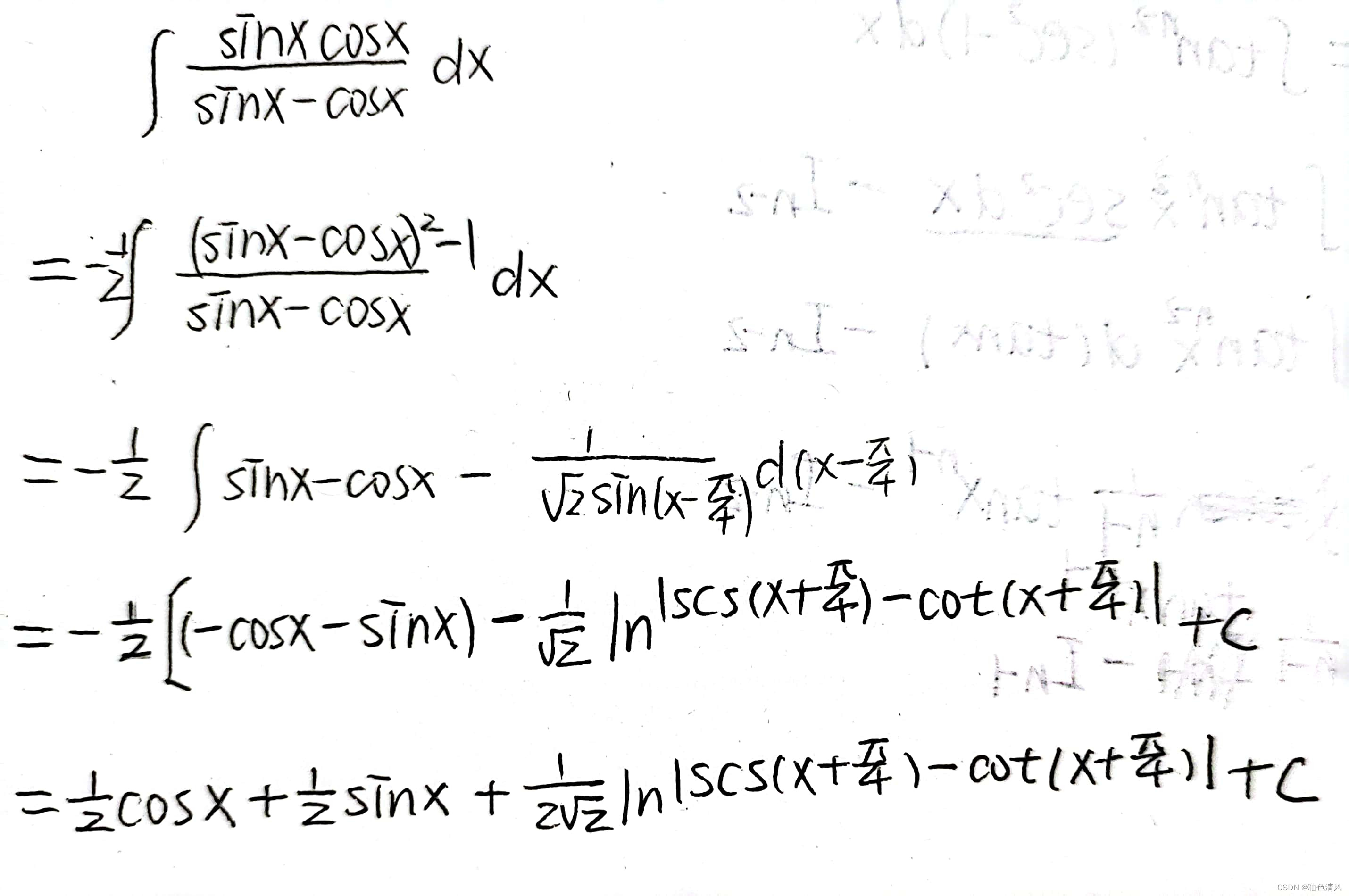
例题(2)
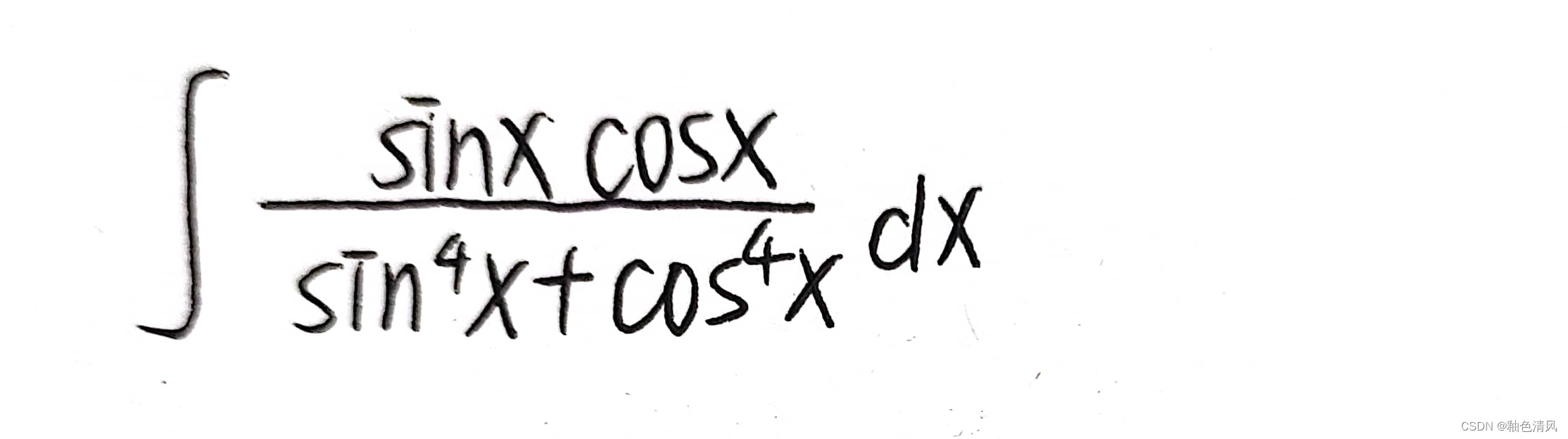
看到这道题,首先的反应是分母的次数高,要降次。
对于一般四次方,是不会因式分解的,但是sin⁴x和cos⁴x是比较特殊。
可以把sin⁴x+cos⁴x写成(sin²x+cos²x)²-2sin²xcos²x
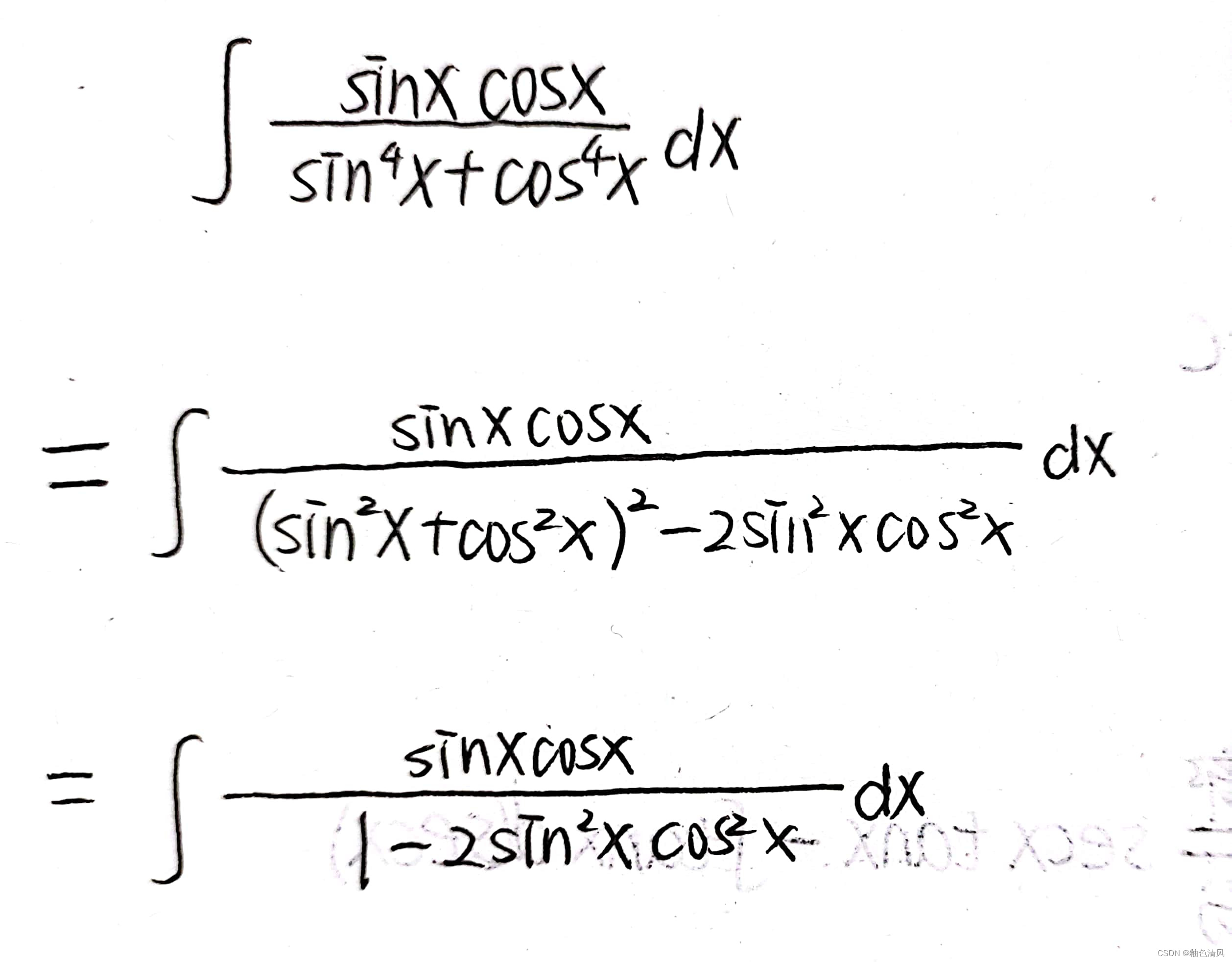
这时,分母的次数还是四次,可以利用二倍角公式降次。
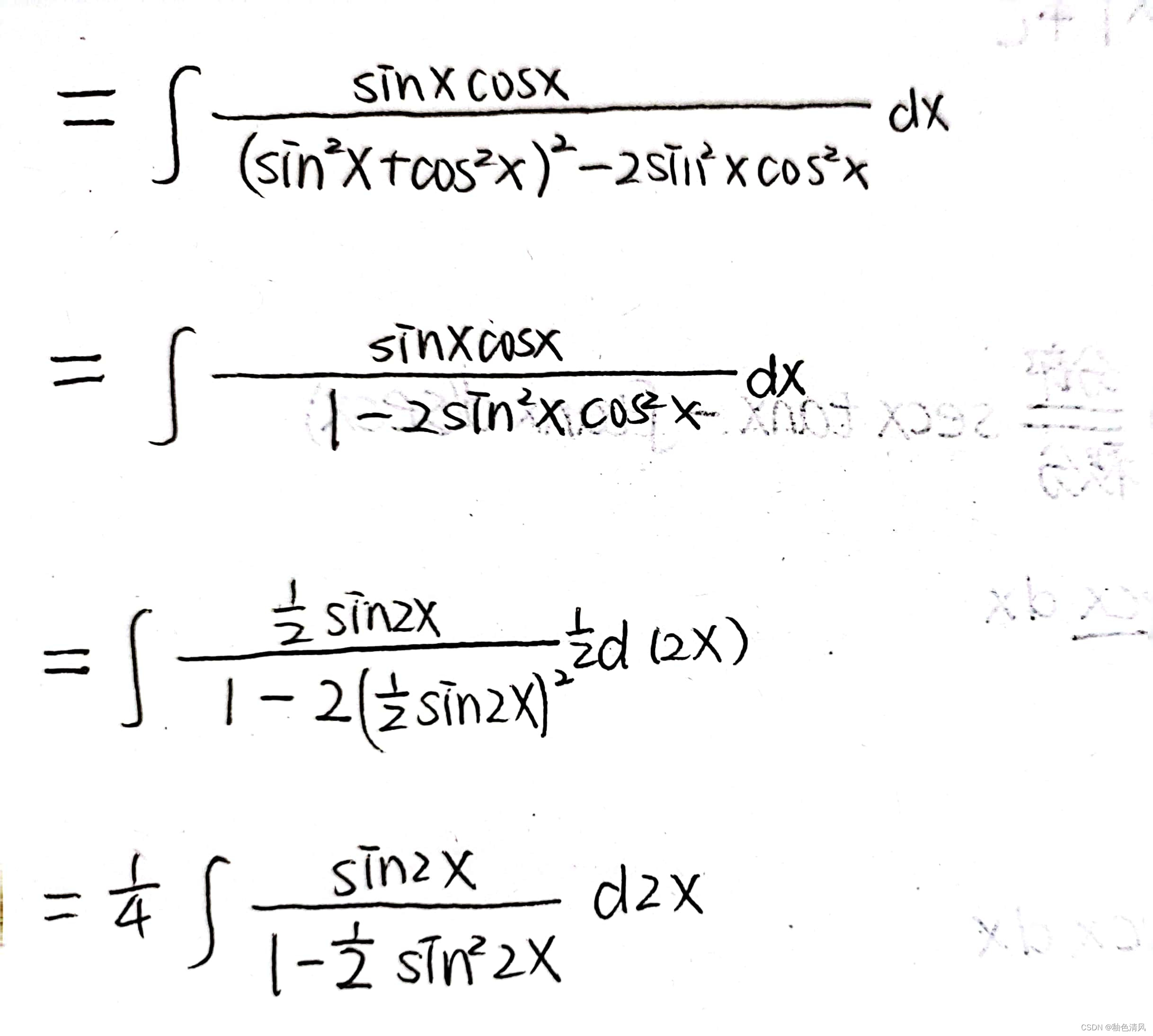
这时,观察,可以将sin2x和d2x凑成-dcos2x
完整过程如下
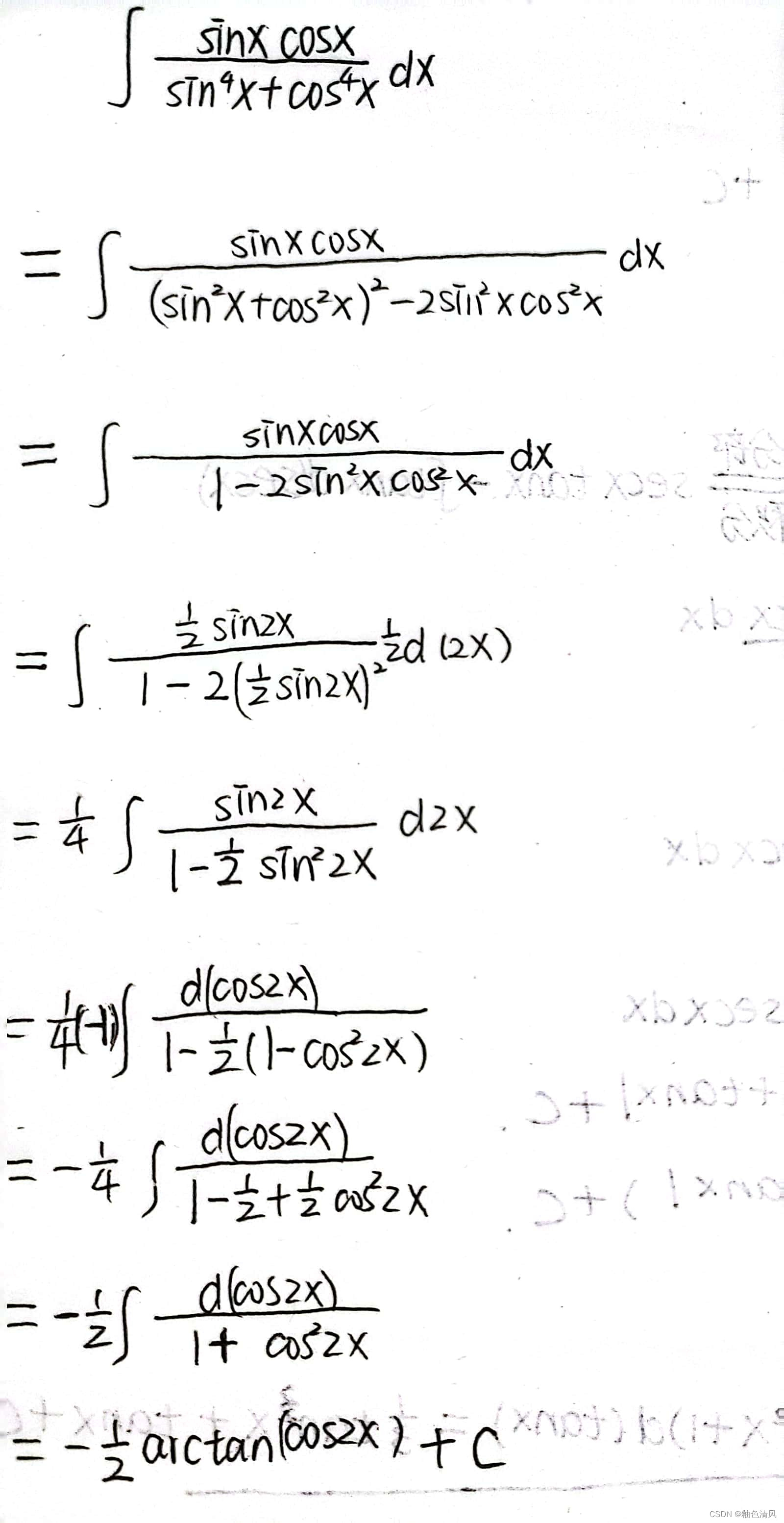
例题(3)
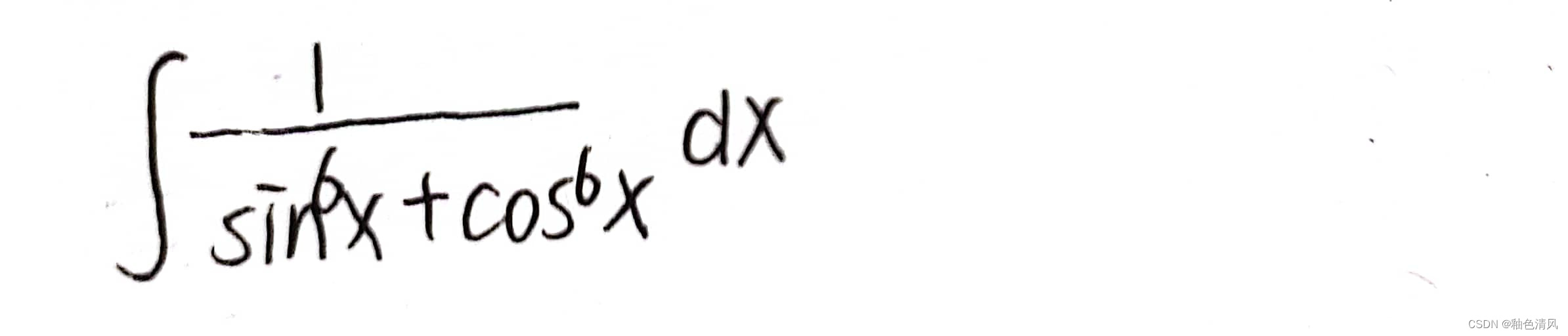
分母为6次,联想到立方和公式(我是第一次没想到这么处理)
下是完整过程(+批注)

例题(4)
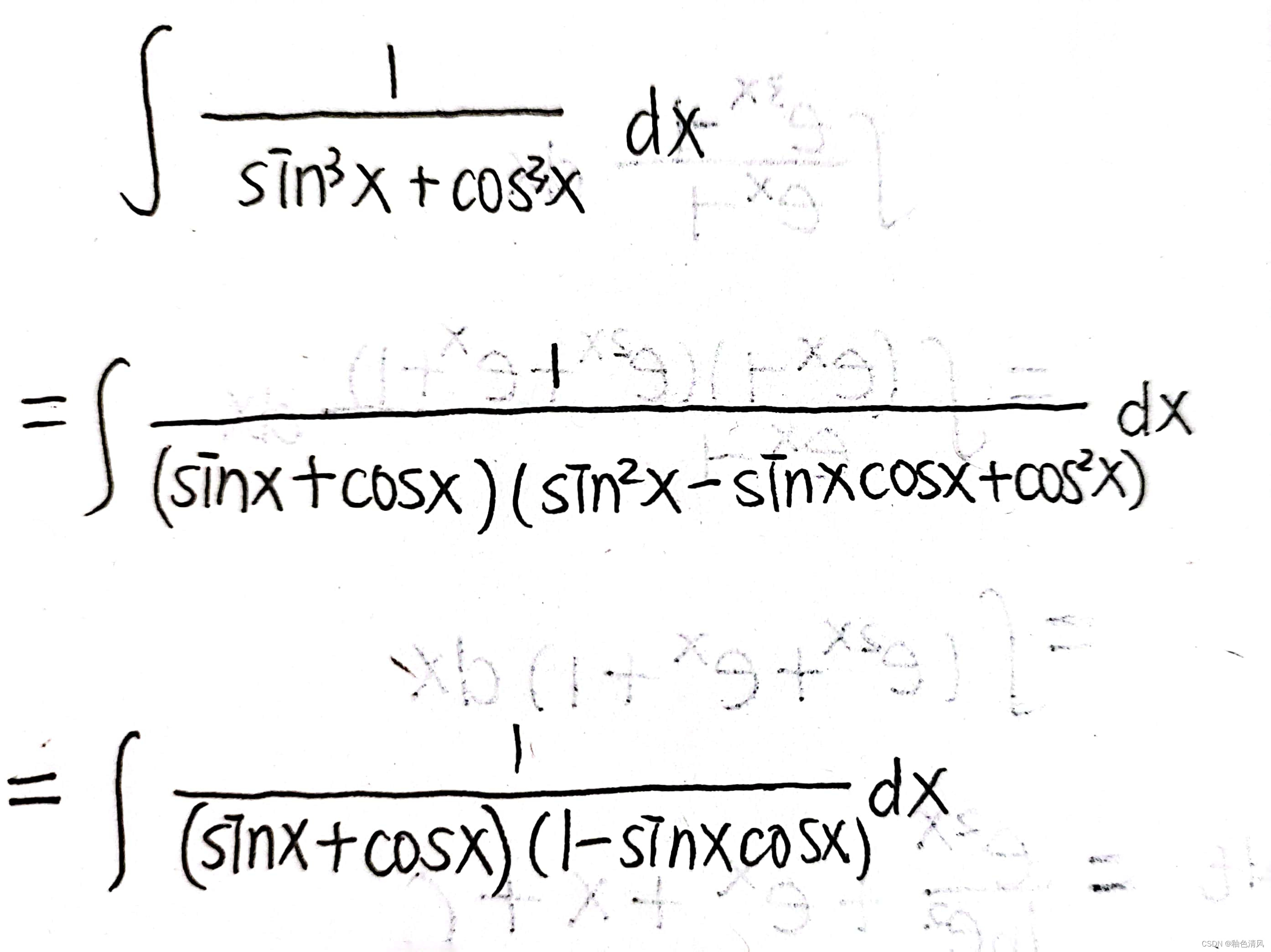
如上题目,利用立方和公式展开。
做到上面👆这一步,这时,观察到分子形式简单,只是分母形式较为繁琐,联想到有理函数。如果能够裂项就好了……
有理函数有固定的裂项方法,但是三角函数呢,好像不太……
但是可以具体题目具体分析,利用三角函数的恒等变形而具体分析
这道题目,首先观察到分子为“1”,分母为sinx+cos,又有sinxcosx,所以不难想到(sinx+cosx)²=1+2sinxcosx
裂项一定是将分子用分母两项进行表示。分子是常数,即要寻找(sinx+cosx)²与1-sincosx之间的系数关系。
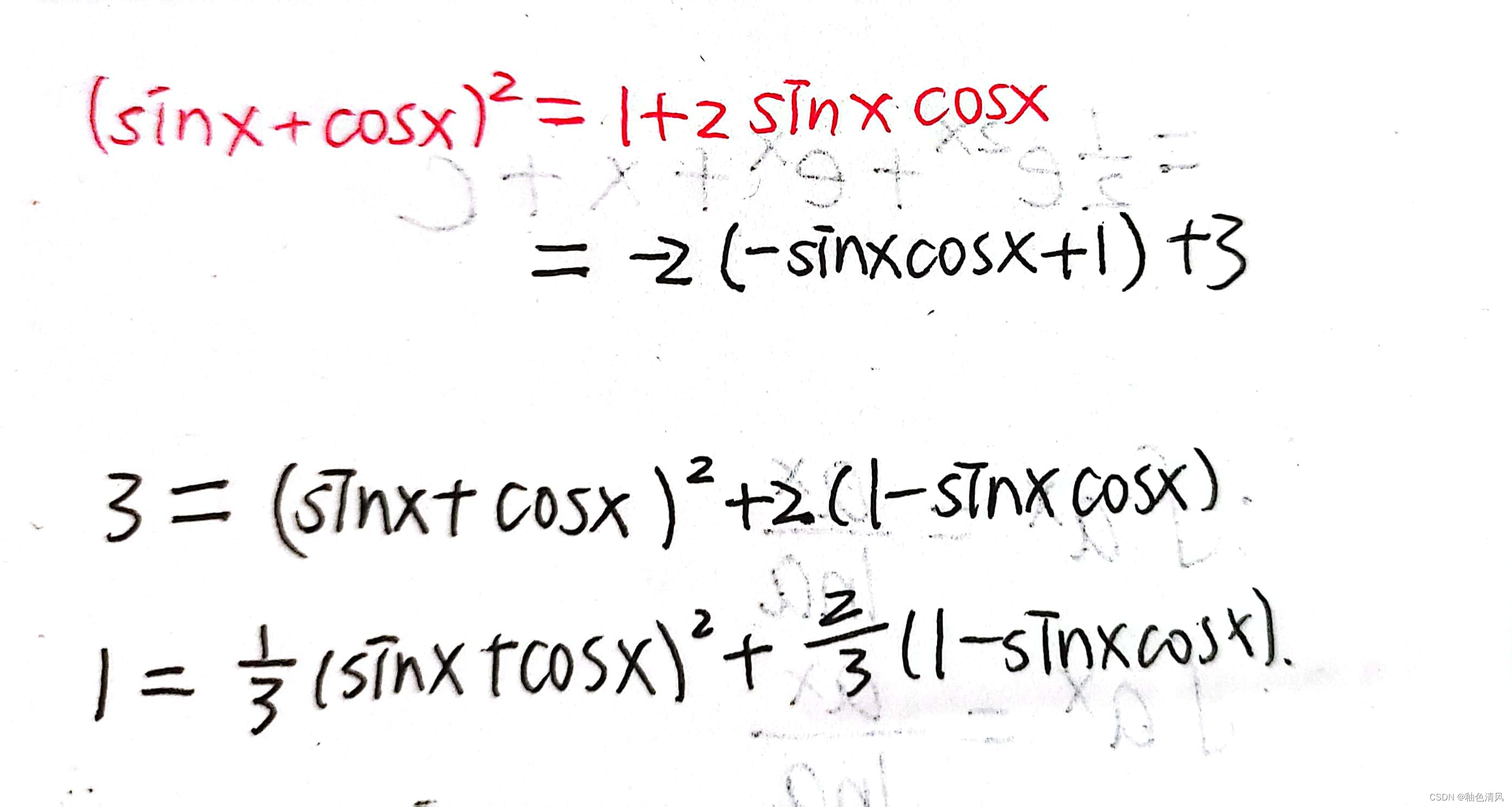
将分子上的“1”替换,原式变为:
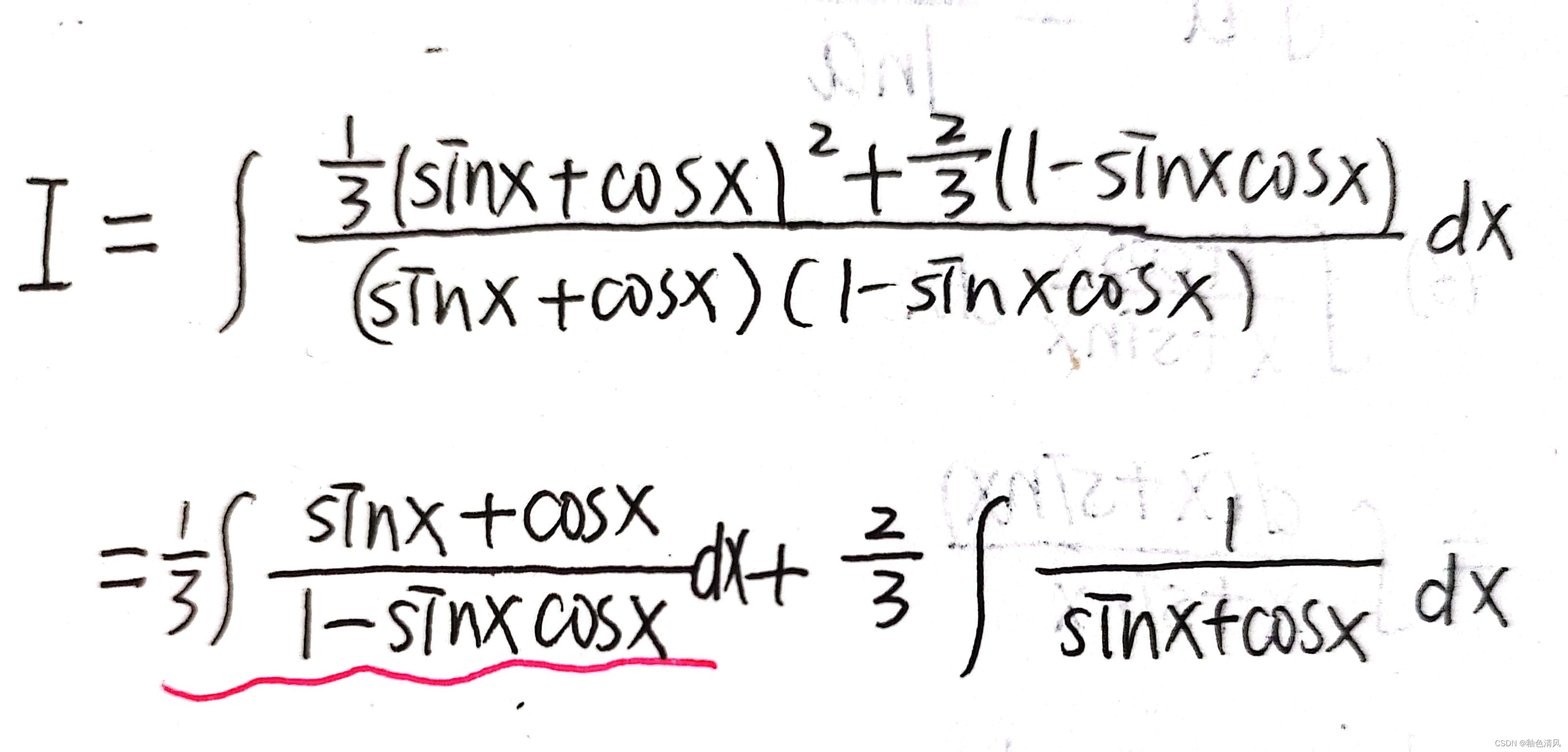
观察到,第二项不定积分很容易求得。
即:
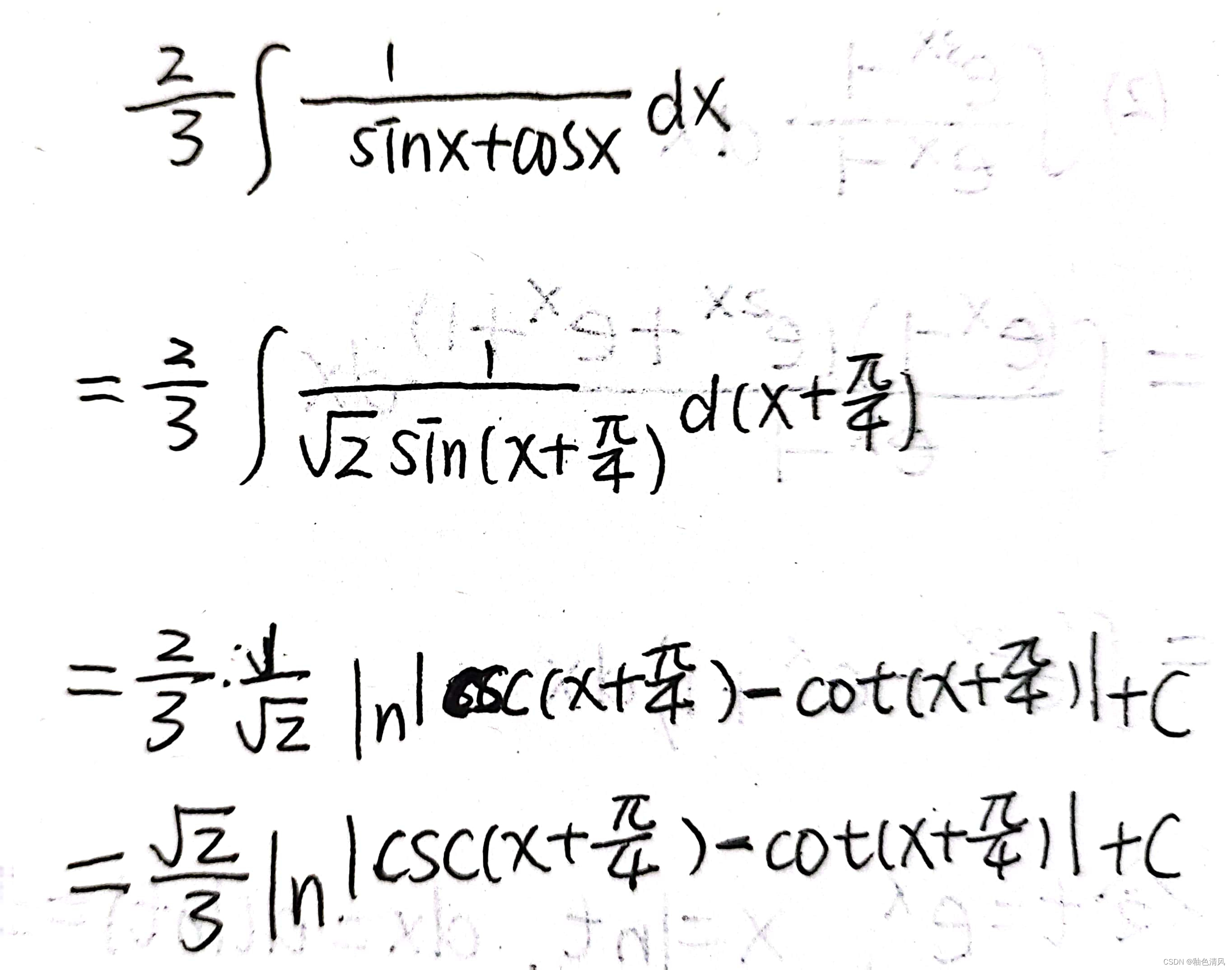
所以,现在要主要解决第一部分的不定积分
✨✨✨✨✨✨(我刚开始并没有想到怎么解决)
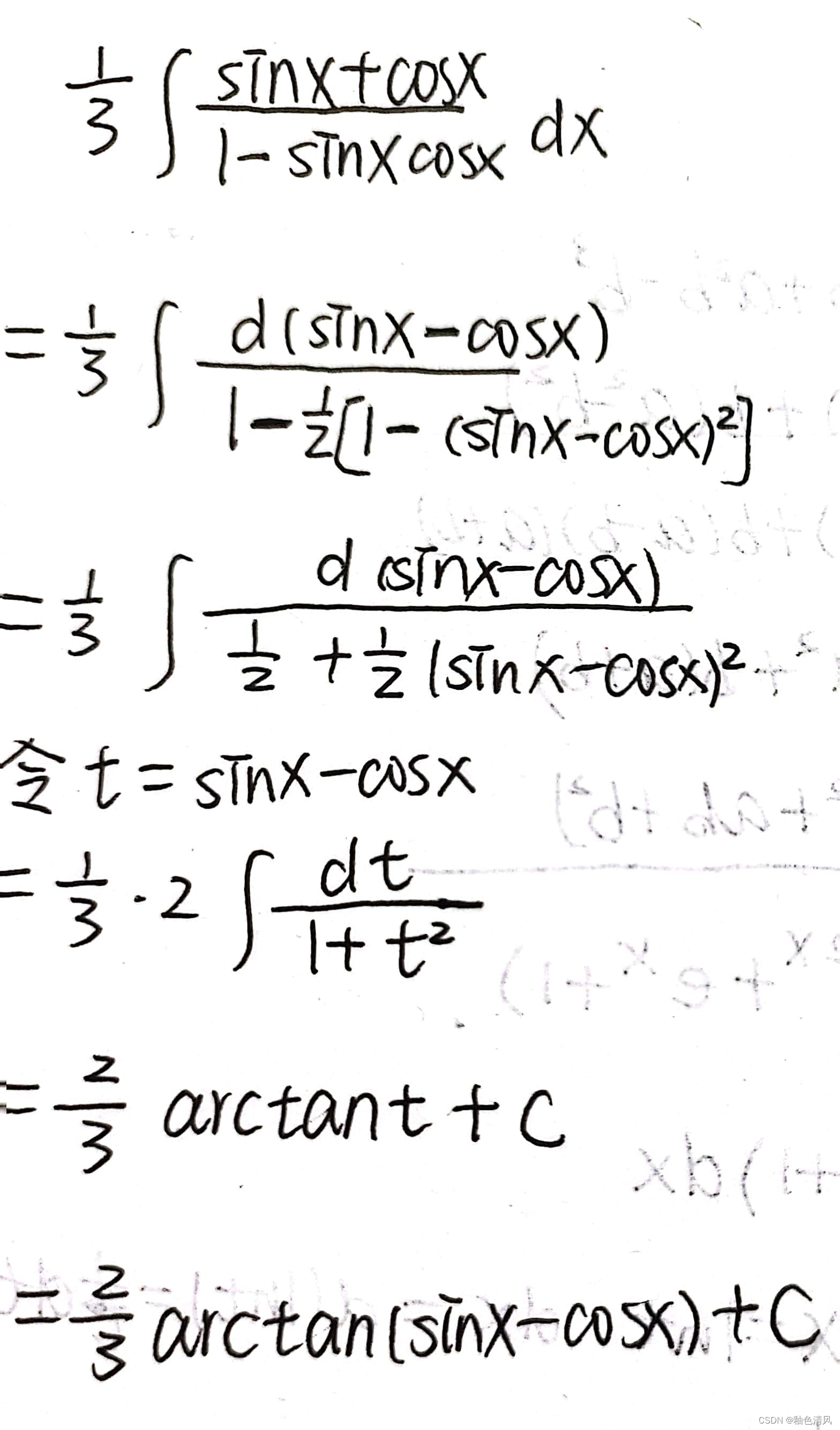
将分子上的sinx+cosx凑到d后面,然后根据三角恒等变形,变换分子下的sinxcosx。
所以,最终
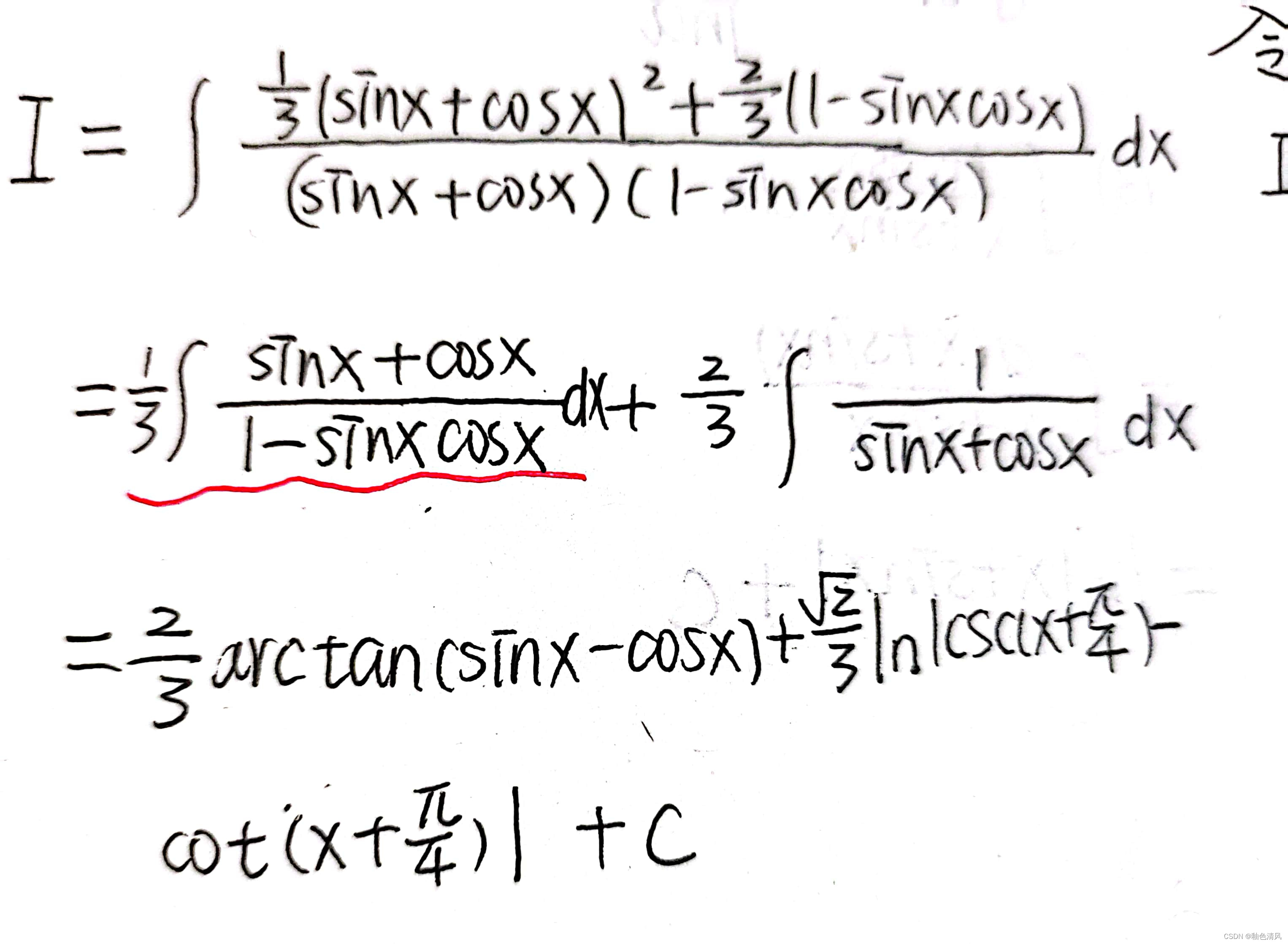








 文章介绍了三角函数积分的一些常见方法,包括积化和差公式、恒等变换的应用,以及如何利用立方和公式、二倍角公式降次。在处理复杂积分问题时,文章强调了具体题目具体分析的重要性,展示了如何通过三角恒等变形和有理函数的裂项技巧来简化问题。
文章介绍了三角函数积分的一些常见方法,包括积化和差公式、恒等变换的应用,以及如何利用立方和公式、二倍角公式降次。在处理复杂积分问题时,文章强调了具体题目具体分析的重要性,展示了如何通过三角恒等变形和有理函数的裂项技巧来简化问题。

















 7456
7456

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










