数据的统计分析及可视化

Manelli.

已于 2025-04-24 23:27:51 修改

阅读量229

点赞数 4

文章标签： python 学习

于 2025-04-24 23:26:24 首次发布

本文链接：https://blog.csdn.net/2302_76372408/article/details/147110370

版权

今天学习了运用python进行的数据统计分析及可视化

一、随机变量及其分布

1.均匀分布及随机数图

（1）均匀分布

加载numpy模块，设置格式

import numpy as np                        #加载numpy包
np.set_printoptions(precision=4)          #设置numpy输出为4位有效数

生成数据集

a=0
b=1
n=20            # n表示在[a,b]中生成n个点
x=np.linspace(a,b,n);   # [a,b]中n个等差数据
# x = np.linspace(0, 1, 20)
x

z = np.ones(n)
y=np.ones(n)/(b-a)
import matplotlib.pyplot as plt               
plt.plot(x,y)
plt.ylim(0,1.5)
plt.stem(x,y)

stem图是一种用于表示离散序列数据的图表，类似于条形图但更加简洁。每个数据点用一根垂直线（茎）表示，而数据值则显示在线的顶部或底部（叶子）。这种类型的图表在信号处理、统计学和工程领域非常常见，因为它可以清晰地展示数据点的位置及其对应的值。

（2）均匀随机数

#生成一个均匀随机实数
np.random.rand(1)   #生成[0,1]上的一个随机实数:random.uniform(0,1) ,每次运行的结果，是不一样的 
#生成一组随机实数及图示
np.random.seed(123)            #设置种子数seed可重复结果,可任意设置
R=np.random.rand(10)
R[:10]  #[0,1]上的1000个随机数=np.random.uniform(0,1,1000) 
plt.plot(R,'.');

示例代码：

# 整数随机数
import random
random.randint(10,20)
# 实数随机数
random.uniform(0,1)
# 整数随机数列
import numpy as np
np.random.randint(10, 21, 9)
# 实数随机数列
np.random.uniform(0,1,10)

2.正态分布及随机数图

（1）正态分布函数

#标准正态分布曲线
from numpy import arange,exp  #arange类似linspace函数
from math import sqrt,pi   
x=arange(-4, 4, 0.1)            #x为-4到4上间距为0.1的数   
y=1/sqrt(2*pi)*exp(-x**2/2)
plt.plot(x,y)

#标准正态分布的取值(pdf)及分位数(ppf)计算
import scipy.stats as st  #加载统计方法包 
p_z=st.norm.pdf(-2)
p_z   #p(z)=1/sqrt(2*pi)*exp(-z**2/2);

za=st.norm.ppf(0.95)
za   #单侧
[st.norm.ppf(0.025),st.norm.ppf(0.975)] #双侧
#标准正态分布的概率计算
p=st.norm.cdf(1.645)
p       #标准正态分布下的面积：p=P(z≤1.645)的累积概率

 #标准正态曲线下[a,b]上计算概率的面积图
import scipy.stats as st  #加载统计方法包 
def norm_p(a,b):            
        x=np.arange(-4,4,0.1) 
        y=st.norm.pdf(x)         
        x1=x[(a<=x) & (x<=b)];x1 
        y1=y[(a<=x) & (x<=b)];y1         
        p=st.norm.cdf(b)-st.norm.cdf(a);
        print("    N(0,1)分布: [%3.2f,%3.2f]  p=%5.4f"%(a,b,p)) 
        plt.plot(x,y);#plt.text(-0.7,0.2,"p=%5.4f"%p,fontsize=15);
        plt.hlines(0,-4,4); plt.vlines(x1,0,y1,colors='r');         
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as st

def norm_p(a, b):
    # 定义x的范围
    x = np.arange(-4, 4, 0.1)
    y = st.norm.pdf(x)
    
    # 计算区间[a, b]内的x和y值
    mask = (a <= x) & (x <= b)
    x1 = x[mask]
    y1 = y[mask]
    
    # 计算累积概率p
    p = st.norm.cdf(b) - st.norm.cdf(a)
    print("N(0,1)分布: [{:.2f},{:.2f}]  p={:.4f}".format(a, b, p))
    
    # 绘制图形
    plt.figure(figsize=(10, 6))
    plt.plot(x, y, label='Standard Normal Distribution PDF')
    plt.fill_between(x1, y1, color='skyblue', alpha=0.5, label=f'Area between {a} and {b}')
    plt.hlines(0, -4, 4, colors='black', linestyles='dashed')
    plt.vlines([a, b], 0, [st.norm.pdf(a), st.norm.pdf(b)], colors='red', linestyle='--')
    
    # 添加标题和标签
    plt.title('Standard Normal Distribution Probability Density Function')
    plt.xlabel('x')
    plt.ylabel('Probability Density')
    plt.legend()
    
    # 显示图形
    plt.grid(True)
    plt.show()

# 示例调用
norm_p(-1, 1)

（2）正态分布随机图

#标准正态随机数及分布图 
np.random.normal(0,1,5)    #生成 5 个标准正态分布随机数

#随机产生1000个标准正态分布随机数，作其概率直方图，然后再添加正态分布的密度函数线。
#np.random.seed(123)             #设置种子数seed可使结果可重复
z1=np.random.normal(0,1,1000)   #1000个标准正态分布随机数N(0,1)
z1[:20]
plt.hist(z1);                   #可设定分段数bins, plt.hist(z1,bins=30)

两张图制作方法

np.random.seed(456)            #设置种子seed可重复结果
z2=np.random.normal(0,1,1000)
plt.hist(z2);#plt.ylim=[0,400];
#做在一张图上
plt.hist(z1)
plt.hist(z2);    
#一页绘制2个正态分布随机图
plt.subplot(121)
plt.hist(z1)
plt.subplot(122)
plt.hist(z2)

import pandas as pd
z12=pd.DataFrame({'z1':z1,'z2':z2})
z12 #构建数据框
z12.plot(kind='hist'); #根据数据框绘直方图
z12.plot(kind='hist',subplots=True,layout=(1,2))
z12.plot(kind='density',subplots=True,layout=(1,2)) #模拟正态分布曲线

#一般正态随机数及分布图
np.random.seed(12)   #设置种子数seed可重复结果
X=np.random.normal(170,10,100)
X.round(1)    #  将数组 X 中的所有元素四舍五入到小数点后一位
import seaborn as sns
sns.distplot(X)

#非正态随机数及分布图
np.random.seed(15)  #设置种子数seed可重复结果
Y=np.random.lognormal(0,1,1000)
Y[:10]
sns.histplot(Y, kde=True)
Z=np.log(Y)      # Z=log(Y)
sns.histplot(Z, kde=True)

（3）正态分布概率检验图

import scipy.stats as st   #加载科学计算包scipy的统计功能
st.probplot(X,plot=plt)

同理可得Y、Z的图像

st.probplot(Y,plot=plt)
st.probplot(Z, plot=plt)

二、统计量及抽样分布图

1.统计量及抽样的概念

（1）简单随机模拟

#生成[0,1]上的一组随机整数
np.random.randint(0,2,10)    #[0,1]上的10个随机整数 
#生成任意区间上的一组随机整数
np.random.randint(1,101,10)  #[1,100]上的10个随机整数数组
np.random.seed(15)           #设置种子数结果可重复
np.random.randint(1,101,10)

（2）随机抽样方法

#根据随机数抽样
import pandas as pd
BSdata=pd.read_excel('./data/DaPy_data.xlsx','BSdata');   #读取学生数据

i=np.random.randint(0,52,6);i #抽取6名学生，取[1,52]上的6个整数
BSdata.iloc[i]                 #获取抽到的6名学生信息 
#直接抽取样本（sample）
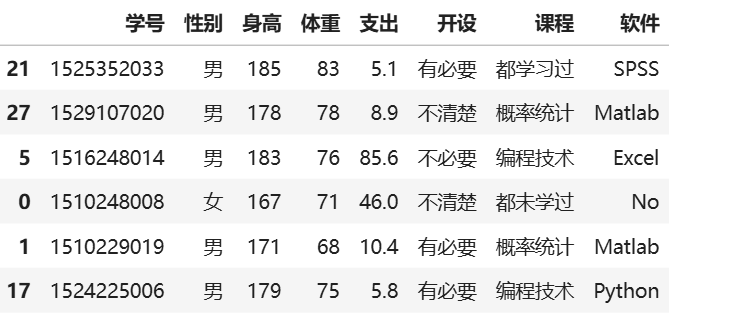
BSdata.sample(6)             #直接抽取名学生及其信息

数据集（部分）：

随机数抽样：

直接抽取样本：

2.统计量的分布

（1）中心极限定理及其模拟图

#正态均值的分布—正态分布 
# 基于正态分布的中心极限定理模拟函数
import seaborn as sns
def norm_sim1(N=1000,n=10):    # n为样本个数，N为模拟次数（即抽样次数） 
    xbar=np.zeros(N)           # 产生放置样本均值的向量  
    for i in range(N):         # 计算[0,1]上的标准正态随机数及均值 
        xbar[i]=np.random.normal(0,1,n).mean() 
    sns.distplot(xbar,bins=50) #plt.hist(xbar,bins=50)   
    print(pd.DataFrame(xbar).describe().T) #模拟结果的基本统计量
np.random.seed(1)         #设置种子数seed使结果可重复
norm_sim1(10000,30)               #根据默认值模拟

#非正态均值统计量的分布 —— 渐近正态分布
# 基于非正态分布的中心极限定理模拟函数
def norm_sim2(N=1000,n=10): 
    xbar=np.zeros(N) 
    for i in range(N):  #计算[0,1]上的均匀随机数及均值 
        xbar[i]=np.random.uniform(0,1,n).mean()  
    sns.distplot(xbar,bins=50)
    print(pd.DataFrame(xbar).describe().T) 
np.random.seed(3)   #设置种子数seed使结果可重复
norm_sim2()

（2）均值的t分布及其图示

#t 分布曲线比较图
x = np.arange(-4,4,0.1)
yn = st.norm.pdf(x,0,1)
yt3 = st.t.pdf(x, 3)
yt10 = st.t.pdf(x, 10)
plt.plot(x, yn, 'r-', x,yt3,'b.',x,yt10,'g-.')
plt.legend(["N(0, 1)", "t(3)", "t(10)"])

三、基本统计推断方法

1.参数的估计方法

（1）点估计

import pandas as pd
BSdata=pd.read_excel('./data/DaPy_data.xlsx','BSdata');   #读取学生数据
#均值的点估计
BSdata['身高'].mean() 

#标准差的点估计
BSdata['身高'].std() 
#比例的点估计
f=BSdata['开设'].value_counts(); 
p=f/sum(f)
p

（2）区间估计

norm_p(-2,2)

# 定义t分布曲线下[a, b]上计算概率的面积图
import scipy.stats as st
def t_p(a,b,df=10):  #t分布曲线下[a,b]上计算概率的面积图
        x=np.arange(-4,4,0.1) 
        y=st.t.pdf(x,df)         
        x1=x[(a<=x) & (x<=b)];x1 
        y1=y[(a<=x) & (x<=b)];y1 
        p=st.t.cdf(b,df)-st.t.cdf(a,df);
        print("      t("+str(df)+"): [%3.2f, %3.2f]  p=%5.4f"%(a,b,p)) 
        plt.plot(x,y);#plt.text(-0.7,0.2,"p=%5.4f"%p,fontsize=15);
        plt.hlines(0,-4,4); plt.vlines(x1,0,y1,colors='r'); 
t_p(-2,2)  #t:[-2,2], df=10

#基于原始数据的t分布均值和置信区间
def t_interval(x,b=0.95):  #这里b为置信水平，通常取95%
    a=1-b 
    n = len(x) 
    ta=st.t.ppf(1-a/2,n-1);ta     
    from math import sqrt 
    se=x.std()/sqrt(n)
    return(x.mean()-ta*se, x.mean()+se*ta)
t_interval(BSdata['身高']) #身高均值的 95%的置信区间

2.参数的假设检验

（1）样本均值t检验

#单样本 t 检验函数进行均值的 t 检验 
print("样本均值：",BSdata.身高.mean())
st.ttest_1samp(BSdata.身高,popmean = 166)

3.统计推断的可视化

（1）均值推断的可视化函数

#定义单样本均值t检验图
def ttest_1plot(X,mu=0,k=0.1): 
    df=len(X)-1  #df=n-1
    t1p=st.ttest_1samp(X, popmean = mu);
    x=np.arange(-4,4,k); y=st.t.pdf(x,df)
    t=abs(t1p[0]);p=t1p[1]
    x1=x[x<=-t]; y1=y[x<=-t];
    x2=x[x>=t]; y2=y[x>=t];
    print("  样本均值： \t%8.4f "%X.mean())
    print("  单样本t检验:    t=%6.3f  p=%6.4f"%(t,p))
    t_interval=st.t.interval(0.95,len(X)-1,X.mean(),X.std())
    print("   t置信区间:\t(%7.4f, %7.4f)"%(t_interval[0],t_interval[1]))
    plt.plot(x,y); plt.hlines(0,-4,4);
    plt.vlines(x1,0,y1,colors='r'); plt.vlines(x2,0,y2,colors='r');
    plt.vlines(st.t.ppf(0.05/2,df),0,0.2,colors='b');
    plt.vlines(-st.t.ppf(0.05/2,df),0,0.2,colors='b');
    plt.text(-0.6,0.2,r"$\alpha$=%3.2f"%0.05,fontsize=15);
ttest_1plot(BSdata.身高,166)  #总体均值为166时的推断图