《概率论与数理统计》第二章总结

星图辛某人

已于 2023-11-02 16:29:38 修改

阅读量381

点赞数

分类专栏：《概率论与数理统计》文章标签：概率论

于 2023-10-22 22:41:28 首次发布

本文链接：https://blog.csdn.net/2302_77272988/article/details/133968370

版权

《概率论与数理统计》专栏收录该内容

6 篇文章 0 订阅

订阅专栏

一、随机变量与分布函数

1.随机变量：设 $X\left ( \omega \right )$ 是定义在概率空间 $\left ( \Omega ,F,P \right )$ 上的单值实函数，即对每个 $\omega \in \Omega$ ，都有 $X\left (\omega \right )\in R$ ，并且对任意 $x\in R$ , $\left \{ \omega :X(\omega )\leq x \right \}$ 都是随机事件，即有

$\left \{ \omega :X(\omega )\leq x \right \}$ $\in F$

则称 $X\left ( \omega \right )$ 为概率空间 $\left ( \Omega ,F,P \right )$ 上的随机变量。通常随机变量 $X\left ( \omega \right )$ 简记为 $X$ ，而事件

$\left \{ \omega :X(\omega )\leq x \right \}$ 简记为 $\left \{ X\leqslant x \right \}$ 。

2.设 $X$ 是概率空间 $\left ( \Omega ,F,P \right )$ 上的随机变量，称函数

$F(x)=P(X\leqslant x)$

为随机变量 $X$ 的概率分布函数，简称为分布函数。通常记为 $X\sim F(x)$ 。

3.概率分布函数的性质：1）单调不减性：若 $a< b$ ，则 $F(a)\leqslant F(b)$

2） $0\leqslant F(x) \leqslant 1$ ，且 $\lim_{x\rightarrow -\infty }F(x)=0,\lim_{x\rightarrow +\infty }F(x)=1,$

3）右连续性： $F(x)$ 在任何点x处右连续。

4.分类：1）离散型随机变量：取值是有限个或像自然数那样无穷可列多个；

2）非离散型随机变量：又可分为连续型随机变量和其它类型随机变量。

二、离散型随机变量及其分布

1.设离散型随机变量X的所有可能取值为 $x_{k}(k=1,2,...)$ ，而X取值 $x_{k}$ 的概率为 $p_{k}$ ，即

$P(X=x_{k})=p_{k},k=1,2,...$

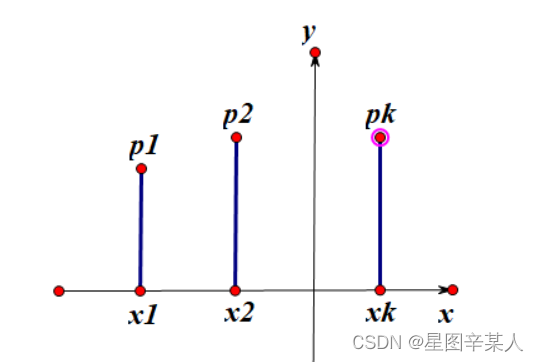
称为离散型随机变量X的概率分布或分布律。把X可能取的值及相应的概率列成表，称为X的概率分布表，或分布列。

随机变量的概率分布是指随机变量所有可能取的值与那些值的概率之间的一种对应关系，这种对应关系可以用解析式、分布列和图示法表示。

2.对于离散型随机变量，概率分布中 $p_{k}$ 必须满足下列性质：

1） $p_{k}\geqslant 0,k=1,2,...$

2） $\sum_{k}^{}p_{k}=1$

反过来，如果满足这两个性质的 $p_{k}$ 也一定可以作为某个离散型随机变量的概率分布。

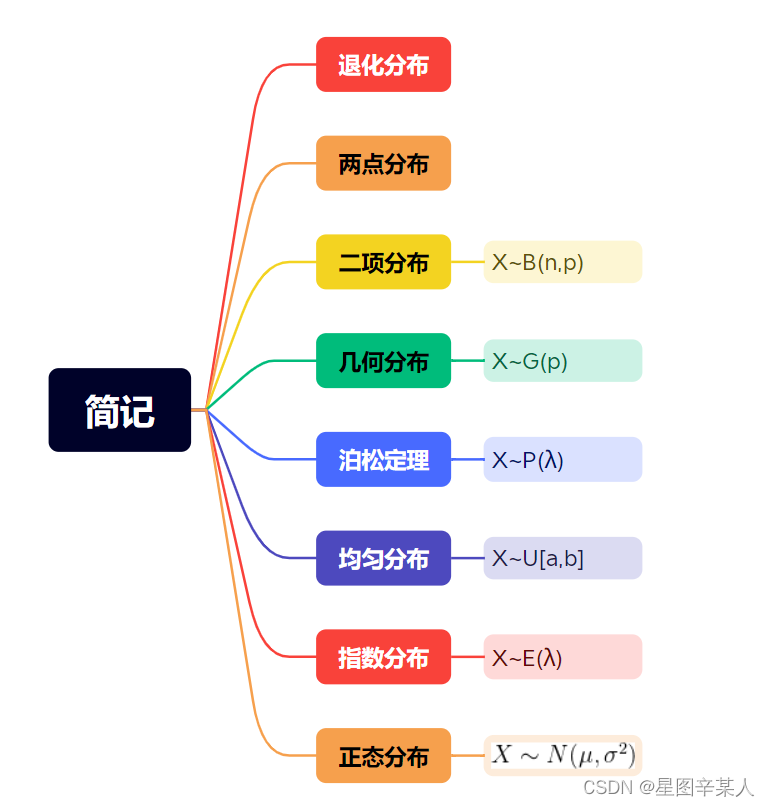
3.几种常见的离散型随机变量：

1）退化分布：

若随机变量X取常数值C的概率为1，即 $P(X=C)=1$ ，则称X服从退化分布。

2）两点分布：

设在一次伯努利试验中， $P(A)=p,P(\overline{A})=q=1-p$ ，若用X记事件A出现的次数，则X的分布列为

或 $P(X=k)=p^{k}q^{1-k}$ ， $k=0,1$ 称X服从两点分布或(0-1)分布。

3）二项分布：

在n重伯努利试验中，若事件A出现的次数记为X，随机变量X可能的值是0,1,2,...,n，相应概率分布为

$P(X=k)=C_{n}^{k}p^{k}q^{n-k},k=0,1,2,...,n$

式中 $p=P(A)$ ，且 $0< p< 1,q= 1-p$ ，则称X服从参数为n,p的二项分布，记作 $X\sim B(n,p)$ .

二项分布的最可能出现次数为 $\left [ (n+1)p \right ]$ 。

4）几何分布：

在伯努利试验中，考虑事件A首次出现时的试验次数X的分布。X的所有可能取值是集合 $\left \{ 1,2,...,n,... \right \}$ ，事件 $\left \{ X=k \right \}$ 表示A首次出现是在第k次试验，即前k-1次试验都出现 $\overline{A}$ ，而第k次试验出现A，这一事件的概率为

$P(X=k)=q^{k-1}p,k=1,2,...,n,...$

上式是几何级数的一般项，因此称为几何分布。记作 $X\sim G(p),0<p<1$ 。显然有

$\sum_{k=1}^{\infty }P(X=k)=\sum_{k=1}^{\infty }q^{k-1}p=p\sum_{k=1}^{\infty }q^{k-1}=p\frac{1}{1-q}=1$

几何分布给出了等待事件A出现共试验了k次的概率。

5）超几何分布：

现有N件产品，其中有M件次品，今从中任取n件(不放回抽取)，则这n件中所含的次品数X是一离散型随机变量，其概率分布为

$P\left \{ X=k \right \}=\frac{C_{M}^{k}C_{N-M}^{n-k}}{C_{N}^{n}}$

其中 $l=min\left \{ M,n \right \}$ 。通常称这个概率分布为超几何分布。记作 $X\sim H(N,n,M)$ 。

4.泊松定理：

设随机变量 $X_{n}(n=1,2,...)$ 服从参数 $n,p_{n}$ 的二项分布，若 $\lim_{n\rightarrow \infty }np_{n}=\lambda$ ，则有

$\lim_{n\rightarrow \infty }P(X_{n}=k)=\frac{\lambda ^{k}}{k!}e^{-\lambda }$

在实际应用中当 $n>10,p<0.1$ 就可以使用泊松定理近似地计算二项分布的概率。

5.泊松分布：

如果随机变量X的概率分布为

$P(X=k)=\frac{\lambda ^{k}}{k!}e^{-\lambda },k=0,1,2,...$

式中 $\lambda >0$ 是常数，则称X服从以 $\lambda$ 为参数的泊松分布，记作 $X\sim P(\lambda )$ 。

自然界中的很多稀疏现象都服从或近似服从泊松分布，所以泊松分布又称为稀疏现象律。

泊松分布的最可能值为 $\left [ \lambda \right ]$ ，若 $\lambda$ 为整数，则最可能值为 $\lambda$ 或 $\lambda -1$ .

三、连续型随机变量及其分布

1.连续型随机变量：在非离散型随机变量中，有一类随机变量可能的取值范围是一个区间或几个区间的并，而且其分布函数可用积分的形式表示。

2.设随机变量X的概率分布函数为 $F(x)$ ，如果存在一个函数 $f(x)$ ，对于任意的实数x，都有

$F(x)=\int_{-\infty }^{x}f(t)dt,-\infty <x<+\infty$

则称X为连续型随机变量，f(x)为X的概率密度函数，简称为概率密度或密度函数。

3.密度函数f(x)具有性质：1） $f(x)\geqslant 0$ 2) $\int_{-\infty }^{+\infty }f(t)dt=1$

满足上述性质的函数f(x)也一定可以作为某一随机变量的概率密度函数。

4. 连续型变量取一特定值a的概率为0，即 $P(X=a)=0$ 。

在计算连续型变量落在某一区间内的概率时，不必区分是开区间还是闭区间。

一个事件的概率为0，这个事件不一定是不可能事件。同样一个事件的概率等于1，这个事件也不一定是必然事件。

5.均匀分布：若连续型随机变量X的概率密度函数为

$f(x)=\left\{\begin{matrix} \frac{1}{b-a},a\leqslant x\leqslant b\\0, else \end{matrix}\right.$

则称X在区间 $\left [ a,b \right ]$ 上服从均匀分布，记作 $X\sim U\left [ a,b \right ]$ 。

服从均匀分布的随机变量X取值落在 $\left [ a,b \right ]$ 内任一区间 $\left [ c,d \right ]$ 内的概率与该区间的长度成正比，而与区间的位置无关，即取值在 $\left [ a,b \right ]$ 上是均匀的。

6.指数分布：

若连续型随机变量X的密度函数为

$f(x)=\left\{\begin{matrix} \lambda e^{-\lambda x},x>0\\0,x\leqslant 0 \end{matrix}\right.$

其中 $\lambda >0$ 为常数，则称X服从参数为 $\lambda$ 的指数分布，记作 $X\sim E(\lambda )$ 。其分布函数为

$F(x)=\left\{\begin{matrix} 1- e^{-\lambda x},x>0\\0,x\leqslant 0 \end{matrix}\right.$

指数分布在研究”寿命“一类问题有很重要的应用，这些”寿命“都近似服从指数分布，其中参数 $\lambda$ 表示平均寿命的倒数。

无记忆性： $P(X>s+t|X>s)=P(X>t)$

如果某人年龄已经s岁，则他再存活t年的概率与年龄s无关。

7.正态分布：

若随机变量X的概率密度函数为

$f(x)=\frac{1}{\sqrt{2\pi }\sigma }e^{-\frac{(x-\mu )^{2}}{2\sigma ^{2}}},-\infty <x<+\infty$

其中 $\mu ,\sigma$ 为常数，且 $\sigma >0$ ，则称随机变量X服从参数为 $\mu ,\sigma$ 的正态分布，记为 $X\sim N(\mu ,\sigma ^{2})$ 。服从正态分布的随机变量又称为正态变量。

当参数 $\mu =0,\sigma =1$ 时，正态分布称为标准正态分布，记为 $X\sim N(0,1)$ ，相应的概率密度函数和分布函数分别特记为 $\varphi (x),\Phi (x)$ 。正态分布又称为高斯分布或者高斯-拉普拉斯分布。 $\mu$ 称为位置参数； $\sigma$ 称为离散参数，越小函数越陡峭。