《概率论与数理统计》第六章总结

星图辛某人

于 2023-12-29 00:22:29 发布

阅读量1.1k

点赞数 22

分类专栏：《概率论与数理统计》文章标签：概率论

本文链接：https://blog.csdn.net/2302_77272988/article/details/135049715

版权

《概率论与数理统计》专栏收录该内容

6 篇文章 0 订阅

订阅专栏

一、参数的点估计

1、参数估计和假设检验是统计推断的核心内容，它们具有深刻的统计思想内涵，是各种数理统计方法的基础。

2、在很多情况下，人们根据经验对总体的分布形式是可以事先确定的，但对其中的某些参数(比如总体均值、方差等)并不清楚。参数估计就是根据样本对总体未知参数的取值进行估计的一种统计推断方法。本节中使用 $\theta$ 表示总体的待估参数， $\Theta$ 表示参数空间，也就是 $\theta$ 所有可能取值的集合。

3、参数估计的形式有两种：

（1）一种是点估计，就是根据样本构造一个统计量 $\widehat{\theta }=\widehat{\theta }(X_{1},X_{2},...,X_{n})$ ，然后用 $\widehat{\theta }$ 去估计 $\theta$ 。称 $\widehat{\theta }(X_{1},X_{2},...,X_{n})$ 为 $\theta$ 的估计量，称 $\widehat{\theta }(x_{1},x_{2},...,x_{n})$ 为 $\theta$ 的估计值。点估计有两种常用方法，矩估计法、最大似然估计法。

（2）另一种是区间估计，就是根据样本构造两个统计量 $\widehat{\theta }_{1}$ 和 $\widehat{\theta }_{2}$ ，且 $\widehat{\theta }_{1}$ < $\widehat{\theta }_{2}$ ，然后用区间 $[\widehat{\theta }_{1},\widehat{\theta }_{2}]$ 估计 $\theta$ ，并对事件“区间 $[\widehat{\theta }_{1},\widehat{\theta }_{2}]$ 包含 $\theta$ ”发生的概率给予一定的保证。

4、矩估计法是用样本的k阶原点矩作为总体的k阶原点矩的估计，进而求解未知参数的一种估计方法。步骤为：

设总体X的未知参数 $\theta =(\theta _{1},\theta _{2},...,\theta _{m})$ 。总体X的k阶原点矩 $E(X^{k})(k\leqslant m)$ 存在，它们显然是 $\theta$ 的函数，不妨记 $\widetilde{A}_{k}(\theta _{1},\theta _{2},...,\theta _{m})=E(X^{k})$ 。设样本 $X_{1},X_{2},...,X_{n}$ 的k阶原点矩为 $A_{k}$ 。根据大数定律， $E(X^{k})(k\leqslant m)$ 的一个合理的估计是样本的k阶原点矩 $A_{k}$ 。故有方程组

$\left\{\begin{matrix} \widetilde{A}_{1}(\theta _{1},\theta _{2},...,\theta _{m})=A_{1}, \\ \widetilde{A}_{2}(\theta _{1},\theta _{2},...,\theta _{m})=A_{2}, \\ .................... \\ \widetilde{A}_{m}(\theta _{1},\theta _{2},...,\theta _{m})=A_{m} \end{matrix}\right.$

若上述方程式有唯一解 $\widehat{\theta }=(\widehat{\theta }_{1},\widehat{\theta }_{2},...,\widehat{\theta }_{m})$

则得到的估计量 $(\widehat{\theta }_{1},\widehat{\theta }_{2},...,\widehat{\theta }_{m})$ 称为未知参数的 $(\theta _{1},\theta _{2},...,\theta _{m})$ 的矩估计量。

不论总体服从什么分布，其均值的矩估计量就是样本均值，方差的矩估计量与样本方差相差一个因子 $\frac{n-1}{n}$ 。

矩估计法只要求知道总体的适当阶原点矩存在，并不要求知道总体的分布类型，但是矩估计法有两点不足：一是求解所要求的总体的某阶原点矩可能不存在，二是求解方程组可能很困难。

5、最大似然估计：设总体X含有待估参数 $\theta =(\theta _{1},\theta _{2},...,\theta _{m})$ ，参数空间为 $\Theta$ 。我们要在 $\Theta$ 中选取一个 $\widehat{\theta }$ ，使得 $\theta =\widehat{\theta }$ 时，样本观测结果即事件 $\left \{ X_{1}=x_{1},X_{2}=x_{2},...,X_{n}=x_{n} \right \}$ 出现的概率 $L(\theta )$ 达到最大值，我们称 $\widehat{\theta }$ 为 $\theta$ 的最大似然估计。

求最大似然估计关键有两步：一是 $L(\theta )$ 的表达式，二是 $L(\theta )$ 的极值解。

（1）若总体X是离散型的， $L(\theta )=\prod_{i=1}^{n}p(x_{i};\theta )$

（2）若总体X是连续型的， $L(\theta )=\prod_{i=1}^{n}f(x_{i};\theta )$

称 $L(\theta )$ 为样本的似然函数。求 $L(\theta )$ 的最大值解常需要求导，为求导方便，一般对似然函数求对数 $lnL(\theta )$ ，称之为对数似然函数。 $\theta$ 的最大似然估计 $\widehat{\theta }$ 可有由似然方程

$\frac{\partial lnL(\theta )}{\partial \theta _{i}}=0,i=1,2,...,m$ 解得

注：求解似然方程(组)得到 $\widehat{\theta }$ 后，还需要验证 $L(\theta )$ 在 $\widehat{\theta }$ 处是否取最大值。另外，有时 $L(\theta )$ 不是 $\theta$ 的连续可导函数，有时参数空间是有界区域，此时不能用求解似然方程(组)的方法，一般利用定义进行判断分析求解。矩估计和最大似然估计有时并不一致。

6、参数的点估计是构造一个统计量作为参数取值的估计，矩估计法和最大似然估计法只是构造参数统计量的两种常用方法。与参数的真值偏离程度越小的估计量越好。通常用偏差平方的期望 $E(\widehat{\theta }-\theta )^{2}$ 来衡量估计量 $\widehat{\theta }$ 的偏离程度，并称为均方误差(MSE)，记作 $MSE(\widehat{\theta })=E(\widehat{\theta }-\theta )^{2}$ 。显然，均方误差越小的估计量越好。如果存在一个估计量 $\widehat{\theta }$ ，在所有的估计量中，它的均方误差最小，则称 $\widehat{\theta }$ 为 $\theta$ 的最优估计量。均方误差可分解为两项 $MSE(\widehat{\theta })=D(\widehat{\theta })+[E(\widehat{\theta })-\theta ]^{2}$

（1）无偏性：设 $\widehat{\theta }=\widehat{\theta }(X_{1},X_{2},...,X_{n})$ 是未知参数 $\theta$ 的估计量。若 $E(\widehat{\theta })=\theta$ ，则称 $\widehat{\theta }$ 是 $\theta$ 的无偏估计，否则称为有偏估计。若 $\lim_{n\rightarrow \infty }E(\widehat{\theta })=\theta$ ，则称 $\widehat{\theta }$ 是 $\theta$ 的渐近无偏估计。

只要总体均值存在，样本均值总是它的无偏估计；只要总体方差存在，样本方差总是其无偏估计。

（2）有效性：设 $\widehat{\theta }_{1}=\widehat{\theta }_{1}(X_{1},X_{2},...,X_{n})$ ， $\widehat{\theta }_{2}=\widehat{\theta }_{2}(X_{1},X_{2},...,X_{n})$ 都是参数 $\theta$ 的无偏估计，如果 $D(\widehat{\theta }_{1})<D(\widehat{\theta }_{2})$ ，则称估计量 $\widehat{\theta }_{1}$ 和 $\widehat{\theta }_{2}$ 有效。进一步，若对于 $\theta$ 的任一无偏估计 $\widehat{\theta }$ ，有 $D(\widehat{\theta }_{1})\leqslant D(\widehat{\theta })$ ，则称 $\widehat{\theta }_{1}$ 是 $\theta$ 的最小方差无偏估计。

（3）相合性(一致性)：设对每一个自然数n，统计量 $\widehat{\theta }_{n}(X_{1},X_{2},...,X_{n})$ 都是未知参数 $\theta$ 的一个估计量，若对任意的 $\varepsilon >0$ ，有 $\lim_{n\rightarrow \infty }P(\left | \widehat{\theta }-\theta \right |\geqslant \varepsilon )=0$ ，则称 $\widehat{\theta }_{n}$ 是 $\theta$ 的相合(一致)估计。

设 $\widehat{\theta }_{n}$ 是 $\theta$ 的一个估计量，若 $\lim_{n\rightarrow \infty }E(\widehat{\theta }_{n})=\theta ,\lim_{n\rightarrow \infty }D(\widehat{\theta }_{n})=0$ ，则 $\widehat{\theta }_{n}$ 是 $\theta$ 的相合估计。

二、参数的区间估计

1、设 $\widehat{\theta }_{1}=\widehat{\theta }_{1}(X_{1},X_{2},...,X_{n})$ ， $\widehat{\theta }_{2}=\widehat{\theta }_{2}(X_{1},X_{2},...,X_{n})$ 是两个统计量，且 $\widehat{\theta }_{1}< \widehat{\theta }_{2}$ ， $\theta$ 是总体X的未知参数，若对给定的 $\alpha \epsilon (0,1)$ ，有 $P(\widehat{\theta }_{1}\leqslant \theta \leqslant \widehat{\theta }_{2})=1-\alpha$ 。则称随机区间 $[\widehat{\theta }_{1},\widehat{\theta }_{2}]$ 是 $\theta$ 的一个区间估计或置信区间。 $\widehat{\theta }_{1}$ 和 $\widehat{\theta }_{2}$ 分别称为置信下限、置信上限， $1-\alpha$ 称为置信水平或置信度。

置信区间的长度描述了估计的“精确性”。置信区间的长度越小，则估计越精确；置信区间的长度越大，则估计越不精确。一般来说，当样本容量n固定后，置信水平要求越高，则精确性(置信区间的长度)就越差。处理的方法是固定置信水平，精确性尽可能地高，也可以增加样本容量n，使得置信水平和精确性都达到满意地要求。

2、求解置信区间的方法：

（1）找一个与要估计的参数 $\theta$ 有关的统计量T，一般是 $\theta$ 的一良好点估计 $\widehat{\theta }$ ；

（2）设法找出T和 $\theta$ 的某一函数 $H(T,\theta )$ ，要求 $H(T,\theta )$ 的分布已知且与 $\theta$ 无关， $H(T,\theta )$ 称为枢轴变量。

（3）寻找合适的常数c,d,使 $P(c\leqslant H(T,\theta )\leqslant d)=1-\alpha$

（4）将不等式 $c\leqslant H(T,\theta )\leqslant d$ 等价变换为 $\widehat{\theta }_{1}\leqslant \theta \leqslant \widehat{\theta }_{2}$ ，所以 $P(\widehat{\theta }_{1}\leqslant \theta \leqslant \widehat{\theta }_{2})=1-\alpha$

故随机区间 $[\widehat{\theta }_{1}, \widehat{\theta }_{2}]$ 即为参数 $\theta$ 的置信水平为 $1-\alpha$ 的置信区间。

表1 单个正态总体的参数区间估计表(置信水平为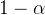 $1-\alpha$ )

待估参数	条件	枢轴变量及其分布	置信区间
均值 $\mu$	方差 $\sigma ^{2}$ 已知	$\frac{\overline{X}-\mu }{\sigma /\sqrt{n}}\sim N(0,1)$	$[\overline{X}-u_{\alpha /2}\frac{\sigma }{\sqrt{n}},\overline{X}+u_{\alpha /2}\frac{\sigma }{\sqrt{n}}]$
均值 $\mu$	方差 $\sigma ^{2}$ 未知	$\frac{\overline{X}-\mu }{S/\sqrt{n}}\sim t(n-1)$	$[\overline{X}-t_{\alpha /2}(n-1)\frac{S }{\sqrt{n}},\overline{X}+t_{\alpha /2}(n-1)\frac{S}{\sqrt{n}}]$
方差 $\sigma ^{2}$	均值 $\mu$ 已知	$\frac{\sum_{i=1}^{n}(X_{i}-\mu )^{2}}{\sigma ^{2}}\sim \chi ^{2}(n)$	$[\frac{\sum_{i=1}^{n}(X_{i}-\mu )^{2}}{\chi ^{2}_{\alpha /2}(n)},\frac{\sum_{i=1}^{n}(X_{i}-\mu )^{2}}{\chi ^{2}_{1-\alpha /2}(n)}]$
方差 $\sigma ^{2}$	均值 $\mu$ 未知	$\frac{(n-1)S^{2}}{\sigma ^{2}}\sim \chi ^{2}(n-1)$	$[\frac{(n-1)S^{2}}{\chi ^{2}_{\alpha /2}(n-1)},\frac{(n-1)S^{2}}{\chi ^{2}_{1-\alpha /2}(n-1)}]$

表2 两个正态总体均值差、方差比的区间估计表(置信水平为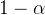 $1-\alpha$ )

待估参数	条件	枢轴变量及其分布	置信区间
$\mu _{1}-\mu _{2}$	$\sigma ^{2}_{1},\sigma ^{2}_{2}$ 已知	$\frac{\overline{X}-\overline{Y}-\left ( \mu _{1}-\mu _{2} \right )}{\sqrt{\frac{\sigma ^{2}_{1}}{m}+\frac{\sigma ^{2}_{2}}{n}}}\sim N(0,1)$	$\begin{matrix} [\overline{X}-\overline{Y}-u_{\alpha /2}\sqrt{\frac{\sigma ^{2}_{1}}{m}+\frac{\sigma ^{2}_{2}}{n}}, \\ \overline{X}-\overline{Y}+u_{\alpha /2}\sqrt{\frac{\sigma ^{2}_{1}}{m}+\frac{\sigma ^{2}_{2}}{n}}] \end{matrix}$
$\mu _{1}-\mu _{2}$	$\sigma ^{2}_{1},\sigma ^{2}_{2}$ 未知，但 $\sigma ^{2}_{1}=\sigma ^{2}_{2}$	$\frac{\overline{X}-\overline{Y}-(\mu _{1}-\mu _{2})}{S_{W}\sqrt{\frac{1}{m}+\frac{1}{n}}}\sim t(m+n-2)$	$\begin{matrix} [\overline{X}-\overline{Y}-t_{\alpha /2}(m+n-2)S_{w}\sqrt{\frac{1}{m}+\frac{1}{n}}, \\ \overline{X}-\overline{Y}+t_{\alpha /2}(m+n-2)S_{w}\sqrt{\frac{1}{m}+\frac{1}{n}}] \end{matrix}$
$\frac{\sigma ^{2}_{1}}{\sigma ^{2}_{2}}$	$\mu _{1},\mu _{2}$ 已知	$\frac{\frac{1}{m}\sum_{i=1}^{m}(X_{i}-\mu _{1})^{2}/\sigma ^{2}_{1}}{\frac{1}{n}\sum_{i=1}^{n}(Y_{i}-\mu _{2})^{2}/\sigma ^{2}_{2}}\sim F(m,n)$	$[\frac{A}{F_{\alpha /2}(m,n)},\frac{A}{F_{1-\alpha /2}(m,n)}]$
$\frac{\sigma ^{2}_{1}}{\sigma ^{2}_{2}}$	$\mu _{1},\mu _{2}$ 未知	$\frac{S^{2}_{1}/\sigma ^{2}_{1}}{S^{2}_{2}/\sigma ^{2}_{2}}\sim F(m-1,n-1)$	$\begin{matrix} [\frac{S^{2}_{1}}{S^{2}_{2}}\frac{1}{F_{\alpha /2}(m-1,n-1)} ,\\ \frac{S^{2}_{1}}{S^{2}_{2}}\frac{1}{F_{1-\alpha /2}(m-1,n-1)}] \end{matrix}$

注：在表2中，符号 $X_{1},X_{2},...,X_{m}$ 表示来自总体 $X\sim N(\mu _{1},\sigma ^{2}_{1})$ 的样本， $Y_{1},Y_{2},...,Y_{n}$ 表示来自总体 $Y\sim N(\mu _{2},\sigma ^{2}_{2})$ 的样本，两样本假定相互独立。 $\overline{X},S_{1}^{2}$ 及 $\overline{Y},S_{2}^{2}$ 分别表示两样本的均值和方差。

$S_{w}^{2}=\frac{(m-1)S_{1}^{2}+(n-1)S_{2}^{2}}{m+n-2},A=\frac{\frac{1}{m}\sum_{i=1}^{m}(X_{i}-\mu _{1})^{2}}{\frac{1}{n}\sum_{i=1}^{n}(Y_{i}-\mu _{2})^{2}}$

三、假设检验

1、已知总体的分布形式，只对总体的某些未知参数取值作出假设，通过抽样来判断假设是否成立，这种检验称为参数检验。如果不知道总体分布的具体类型，只对未知分布函数的类型或者它的某些特性提出假设，然后对这种假设进行检验，这种检验称为非参数检验。参数检验和非参数检验称为假设检验。

2、假设检验的步骤：

（1）建立假设

得到 $H_{0},H_{1}$ ，通常称 $H_{0}$ 为原假设，称 $H_{1}$ 为备选假设。假设检验的目的是在两者之间选择其一。

（2）选取检验统计量

求出 $H_{0}$ 成立时检验统计量的分布，并与 $H_{1}$ 成立时统计量的分布进行比较，从而得到对 $H_{0}$ 不利的事件。

（3）选取检验的显著性水平 $\alpha$ 与临界值，进而确定 $H_{0}$ 的拒绝区域

显著性水平 $\alpha$ 就是所谓的小概率的具体数值，它一般事先给定。临界值表示使对 $H_{0}$ 不利的小概率事件发生的统计量的取值界限。临界值通常根据统计量分布的分位数确定。

（4）作判断

计算统计量的观测值，并与临界值比较，即考察对 $H_{0}$ 不利的小概率事件是否发生。若发生，则拒绝 $H_{0}$ ，接受 $H_{1}$ ；反之，则接受 $H_{0}$ 。

3、原假设与备选假设的选取原则

（1）把研究者要证明的结论作为备选假设 $H_{1}$ ；

（2）把研究者要反对的假设作为原假设 $H_{0}$ ；

（3）把现状作为原假设 $H_{0}$ ；

（4）把不能轻易否定的假设作为原假设 $H_{0}$ 。原假设通常处于“被保护”的地位。

4、可以将假设检验归纳为 $H_{0}:\theta \in \Theta_{0} , ~~H_{1}:\theta \in \Theta_{1}=\Theta -\Theta _{0}$

如果集合 $\Theta _{0}$ 或 $\Theta _{1}$ 为单点集合，则这样的假设称为简单假设，如果集合 $\Theta _{0}$ 或 $\Theta _{1}$ 是多点集合，则这样的假设称为复合假设。

在数轴上，如果集合 $\Theta _{1}$ 位于集合 $\Theta _{0}$ 的两侧，则这种类型的参数检验称为双侧检验；如果集合 $\Theta _{1}$ 位于集合 $\Theta _{0}$ 的右侧，则这种类型的参数检验称为右侧检验；如果集合 $\Theta _{1}$ 位于集合 $\Theta _{0}$ 的左侧，则这种类型的参数检验称为左侧检验；右侧检验和左侧检验统称为单侧检验。

5、犯错误，就是检验得到的结论与实际情况不符。有两种情况： $\beta$

一是原假设 $H_{0}$ 成立，而检验的结果是拒绝了 $H_{0}$ ；

二是备择假设 $H_{1}$ 成立，而检验的结果是接受了 $H_{0}$ 。

（1）当原假设 $H_{0}:\theta \in \Theta_{0}$ 为真时，而样本落在拒绝区域 $V$ 中，根据判别法则，应做出拒绝 $H_{0}$ 的判断，称这类错误为第一类错误或“弃真”错误。犯第一类错误的概率，通常记为 $\alpha$ 。

$\alpha =P(V|H_{0})=P(V|\theta \in \Theta _{0})$

（2）当备择假设 $H_{1}:\theta \in \Theta -\Theta_{0}$ 为真时，而样本落在 $H_{0}$ 的接受区域 $\overline{V}$ 中，根据判别法则，应做出接受 $H_{0}$ 的判断，称这类错误为第二类错误或“存伪”错误。犯第二类错误的概率，通常记为 $\beta$

$\beta =P(\overline{V}|H_{1})=P(\overline{V}|\theta \in \Theta _{1})$

判断结果	实际情况
判断结果	$H_{0}$ 成立	$H_{1}$ 成立
拒绝 $H_{0}$	第一类错误	正确
接受 $H_{0}$	正确	第二类错误

$H_{0},H_{1}$ 给定后，若样本容量n固定， $\alpha$ 取值越小， $u_{\alpha }$ 越大，犯第二类错误的概率 $\beta$ 将越大；若 $\alpha$ 固定，当样本容量n增大时， $\beta$ 的取值将变小。所以要使得 $\alpha ,\beta$ 都达到很小，一般通过适当增加样本容量n来实现。

6、对于一个假设检验问题，当显著性水平 $\alpha$ 给定后，检验的结果要么拒绝原假设要么接受原假设，但显然假设检验的结果受到 $\alpha$ 数值的影响。在假设检验问题中，利用样本观测值能够做出拒绝原假设的最小显著性水平，称为检验的 $p$ 值。

四、正态总体参数的假设检验

1、关于均值 $\mu$ 的检验

（1） $\sigma ^{2}$ 已知

选择 $U=\frac{\overline{X}-\mu _{0}}{\sigma /\sqrt{n}}$ 为检验统计量。当 $H_{0}$ 成立时，统计量 $U\sim N(0,1)$ 。统计量 $U$ 的绝对值偏大，说明 $\overline{X}$ 与 $\mu _{0}$ 相差偏大，此时应拒绝 $H_{0}$ 。

故对于给定的显著性水平 $\alpha$ ，选取临界值 $u_{\alpha /2}$ 满足

$P(\left | U \right |> u_{\alpha /2})=\alpha ,$

从而得到拒绝域为

$V=\left \{ (x_{1},x_{2},...,x_{n}):\left | U(x_{1},x_{2},...,x_{n}) \right |>u_{\alpha /2} \right \}$

这种以 $U$ 作为检验统计量的检验称为 $U$ 检验。

（2） $\sigma ^{2}$ 未知

选择 $T=\frac{\overline{X}-\mu _{0}}{S/\sqrt{n}}$ 作为检验统计量。当 $H_{0}$ 成立时，统计量 $T\sim t(n-1)$ 。统计量 $T$ 的绝对值偏大，说明 $\overline{X}$ 与 $\mu _{0}$ 相差偏大，此时应拒绝 $H_{0}$ 。

故对于给定的显著性水平 $\alpha$ ，选取临界值 $t_{\alpha /2}(n-1)$ 满足

$P(\left | T \right |>t_{\alpha /2}(n-1))=\alpha$

从而得到拒绝域为

$V=\left \{ (x_{1},x_{2},...,x_{n}):\left | T(x_{1},x_{2},...,x_{n}) \right |>t_{\alpha /2}(n-1) \right \}$

这种以 $t$ 分布作为检验统计量的检验称为 $t$ 检验。

2、关于方差 $\sigma ^{2}$ 的检验

（1） $\mu$ 已知

选择 $\chi ^{2}=\frac{\sum_{i=1}^{n}(X_{i}-\mu )^{2}}{\sigma ^{2}}$ 作为检验统计量。当 $H_{0}$ 成立时， $\frac{\sum_{i=1}^{n}(X_{i}-\mu )^{2}}{\sigma ^{2}}\sim \chi ^{2}(n)$ 。检验统计量 $\chi ^{2}$ 的取值偏大或偏小时，说明相差较大，此时应拒绝 $H_{0}$ 。

故对于给定的显著性水平 $\alpha$ ，选取临界值 $\chi ^{2}_{\alpha /2}(n),\chi ^{2}_{1-\alpha /2}(n)$ 分别满足

$P(\chi ^{2}>\chi ^{2}_{\alpha /2}(n))=\frac{\alpha }{2},P(\chi ^{2}<\chi ^{2}_{1-\alpha /2}(n))=\frac{\alpha }{2}$

从而得到拒绝域为

$V=\{ (x_{1},x_{2},...,x_{n}):\chi ^{2}>\chi ^{2}_{\alpha /2}(n)$ 或 $\chi ^{2}<\chi ^{2}_{1-\alpha /2}(n)\}$

这种以 $\chi ^{2}$ 分布作为检验统计量的检验称为 $\chi ^{2}$ 检验。

（2） $\mu$ 未知

选择 $\chi ^{2}=\frac{(n-1)S^{2}}{\sigma ^{2}}$ 作为检验统计量。当 $H_{0}$ 成立时, $\chi ^{2}=\frac{(n-1)S^{2}}{\sigma ^{2}}\sim \chi ^{2}(n-1)$ 。统计量 $\chi ^{2}$ 的取值偏大或偏小时，说明样本方差 $S^{2}$ 与 $\sigma ^{2}_{0}$ 相差偏大，此时应拒绝 $H_{0}$ 。

故对于给定的显著性水平 $\alpha$ ，选取临界值 $\chi ^{2}_{\alpha /2}(n-1),\chi ^{2}_{1-\alpha /2}(n-1)$ 分别满足

$P(\chi ^{2}>\chi ^{2}_{\alpha /2}(n-1))=\frac{\alpha }{2},P(\chi ^{2}<\chi ^{2}_{1-\alpha /2}(n-1))=\frac{\alpha }{2}$

从而得到拒绝域为

$V=\{ (x_{1},x_{2},...,x_{n}):\chi ^{2}>\chi ^{2}_{\alpha /2}(n-1)$ 或 $\chi ^{2}<\chi ^{2}_{1-\alpha /2}(n-1)\}$

这种以 $\chi ^{2}$ 分布作为检验统计量的检验称为 $\chi ^{2}$ 检验。

3、两个正态总体的假设检验

（1） $\mu_{1},\mu _{2}$ 未知，检验假设 $H_{0}:\sigma ^{2}_{1}=\sigma ^{2}_{2};H_{1}:\sigma ^{2}_{1}\neq \sigma ^{2}_{2}$

由于样本方差 $S^{2}$ 是总体方差 $\sigma ^{2}$ 的良好估计，一般情况下二者相差不大。因而当 $H_{0}$ 成立时，比值 $\frac{S^{2}_{1}/\sigma ^{2}_{1}}{S^{2}_{2}/\sigma ^{2}_{2}}$ 的值不应过大，也不应过小，否则就应拒绝 $H_{0}$ 。可选择 $F=\frac{S^{2}_{1}/\sigma ^{2}_{1}}{S^{2}_{2}/\sigma ^{2}_{2}}$ 作为检验统计量。当 $H_{0}$ 成立时， $F=\frac{S^{2}_{1}}{S^{2}_{2}}\sim F(m-1,n-1)$ 。若 $F$ 的取值偏大或偏小，应拒绝 $H_{0}$ 。

故对于给定的显著性水平 $\alpha$ ，选取临界值 $F_{\alpha /2}(m-1,n-1),F_{1-\alpha /2}(m-1,n-1)$ ，分别满足

$P(F>F_{\alpha /2}(m-1,n-1))=\frac{\alpha }{2},P(F<F_{1-\alpha /2}(m-1,n-1))=\frac{\alpha }{2}$

从而得到拒绝域为

$V=\{ (x_{1},x_{2},...,x_{n}):F>F_{\alpha /2}(m-1,n-1)$ 或 $F<F_{1-\alpha /2}(m-1,n-1)\}$

（2） $\sigma ^{2}_{1},\sigma ^{2}_{2}$ 未知，但 $\sigma ^{2}_{1}=\sigma ^{2}_{2}$ ，检验假设 $H_{0}:\mu _{1}=\mu _{2};H_{1}:\mu _{1}\neq \mu _{2}$

选择检验统计量 $T=\frac{\overline{X}-\overline{Y}}{S_{w}\sqrt{\frac{1}{m}+\frac{1}{n}}}\sim t(m+n-2)$ ，其中 $S^{2}_{w}=\frac{(m-1)S^{2}_{1}+(n-1)S^{2}_{2}}{m+n-2}$

表1 单正态总体的假设检验表(显著性水平为 $\alpha$ )

条件	原假设 $H_{0}$	备择假设 $H_{1}$	检验统计量	拒绝域
$\sigma ^{2}=\sigma ^{2}_{0}$ 已知	$\mu =\mu _{0}$	$\mu \neq \mu _{0}$	$U=\frac{\overline{X}-\mu _{0}}{\sigma _{0}/\sqrt{n}}$	$\left \| U \right \|>u_{\alpha /2}$
	$\mu \leqslant \mu _{0}$	$\mu > \mu _{0}$		$U>u_{\alpha }$
	$\mu \geqslant \mu _{0}$	$\mu < \mu _{0}$		$U<-u_{\alpha }$
$\sigma ^{2}$ 未知	$\mu =\mu _{0}$	$\mu \neq \mu _{0}$	$T=\frac{\overline{X}-\mu _{0}}{S/\sqrt{n}}$	$\left \| T \right \|>t_{\alpha /2}(n-1)$
	$\mu \leqslant \mu _{0}$	$\mu > \mu _{0}$		$T >t_{\alpha }(n-1)$
	$\mu \geqslant \mu _{0}$	$\mu < \mu _{0}$		$T <-t_{\alpha }(n-1)$
$\mu =\mu _{0}$ 已知	$\sigma ^{2}=\sigma ^{2}_{0}$	$\sigma ^{2}\neq \sigma ^{2}_{0}$	$\chi ^{2}=\frac{\sum_{i=1}^{n}(X_{i}-\mu_{0} )^{2}}{\sigma_{0} ^{2}}$	$\chi ^{2}>\chi ^{2}_{\alpha /2}(n)$ 或 $\chi ^{2}<\chi ^{2}_{1-\alpha /2}(n)$
	$\sigma ^{2}\leqslant \sigma ^{2}_{0}$	$\sigma ^{2}> \sigma ^{2}_{0}$		$\chi ^{2}>\chi ^{2}_{\alpha }(n)$
	$\sigma ^{2}\geqslant \sigma ^{2}_{0}$	$\sigma ^{2}< \sigma ^{2}_{0}$		$\chi ^{2}<\chi ^{2}_{1-\alpha }(n)$
$\mu$ 已知	$\sigma ^{2}=\sigma ^{2}_{0}$	$\sigma ^{2}\neq \sigma ^{2}_{0}$	$\chi ^{2}=\frac{(n-1)S^{2}}{\sigma _{0}^{2}}$	$\chi ^{2}>\chi ^{2}_{\alpha /2}(n-1)$ 或 $\chi ^{2}<\chi ^{2}_{1-\alpha /2}(n-1)$
	$\sigma ^{2}\leqslant \sigma ^{2}_{0}$	$\sigma ^{2}> \sigma ^{2}_{0}$		$\chi ^{2}>\chi ^{2}_{\alpha }(n-1)$
	$\sigma ^{2}\geqslant \sigma ^{2}_{0}$	$\sigma ^{2}< \sigma ^{2}_{0}$		$\chi ^{2}<\chi ^{2}_{1-\alpha }(n-1)$

表2 两个正态总体的假设检验表(显著性水平为 $\alpha$ )

条件	原假设 $H_{0}$	备择假设 $H_{1}$	检验统计量	拒绝域
$\sigma _{1}^{2},\sigma _{2}^{2}$ 已知	$\mu _{1}=\mu _{2}$	$\mu _{1}\neq \mu _{2}$	$U=\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{\sigma ^{2}_{1}}{m}+\frac{\sigma ^{2}_{2}}{n}}}$	$\left \| U \right \|>u_{\alpha /2}$
	$\mu _{1}\leqslant \mu _{2}$	$\mu _{1}>\mu _{2}$		$U>u_{\alpha }$
	$\mu _{1}\geqslant \mu _{2}$	$\mu _{1}<\mu _{2}$		$U<-u_{\alpha }$
$\sigma _{1}^{2},\sigma _{2}^{2}$ 未知但 $\sigma _{1}^{2}=\sigma _{2}^{2}$	$\mu _{1}=\mu _{2}$	$\mu _{1}\neq \mu _{2}$	$T=\frac{\overline{X}-\overline{Y}}{S_{w}\sqrt{\frac{1}{m}+\frac{1}{n}}}$	$\left \| T \right \|>t_{\alpha /2}(m+n-2)$
	$\mu _{1}\leqslant \mu _{2}$	$\mu _{1}>\mu _{2}$		$T >t_{\alpha }(m+n-2)$
	$\mu _{1}\geqslant \mu _{2}$	$\mu _{1}<\mu _{2}$		$T <-t_{\alpha }(m+n-2)$
$\mu _{1},\mu _{2}$ 已知	$\sigma ^{2}_{1}=\sigma ^{2}_{2}$	$\sigma ^{2}_{1}\neq \sigma ^{2}_{2}$	$F=\frac{\sum_{i=1}^{n}(X_{i}-\mu _{1})^{2}/m}{\sum_{j=1}^{n}(Y_{j}-\mu _{2})^{2}/n}$	$F>F_{\alpha /2}(m,n)$ 或 $F<F_{1-\alpha /2}(m,n)$
	$\sigma ^{2}_{1}\leqslant \sigma ^{2}_{2}$	$\sigma ^{2}_{1}>\sigma ^{2}_{2}$		$F>F_{\alpha }(m,n)$
	$\sigma ^{2}_{1}\geqslant \sigma ^{2}_{2}$	$\sigma ^{2}_{1}<\sigma ^{2}_{2}$		$F<F_{1-\alpha }(m,n)$
$\mu _{1},\mu _{2}$ 未知	$\sigma ^{2}_{1}=\sigma ^{2}_{2}$	$\sigma ^{2}_{1}\neq \sigma ^{2}_{2}$	$F=\frac{S^{2}_{1}}{S^{2}_{1}}$	$F>F_{\alpha /2}(m-1,n-1)$ 或 $F<F_{1-\alpha /2}(m-1,n-1)$
	$\sigma ^{2}_{1}\leqslant \sigma ^{2}_{2}$	$\sigma ^{2}_{1}>\sigma ^{2}_{2}$		$F>F_{\alpha }(m-1,n-1)$
	$\sigma ^{2}_{1}\geqslant \sigma ^{2}_{2}$	$\sigma ^{2}_{1}<\sigma ^{2}_{2}$		$F<F_{1-\alpha }(m-1,n-1)$

星图辛某人

关注

22
点赞
踩
25

收藏

觉得还不错? 一键收藏
1
评论
《概率论与数理统计》第六章总结

和是统计推断的核心内容，它们具有深刻的统计思想内涵，是各种数理统计方法的基础。在很多情况下，人们根据经验对总体的分布形式是可以事先确定的，但对其中的某些(比如总体均值、方差等)并不清楚。就是根据样本对总体未知参数的取值进行估计的一种统计推断方法。本节中使用表示总体的待估参数，表示参数空间，也就是所有可能取值的集合。设总体X的未知参数。总体X的k阶原点矩存在，它们显然是的函数，不妨记。设样本的k阶原点矩为。根据的一个合理的估计是样本的k阶原点矩。故有方程组若上述方程式有唯一解则得到的。
复制链接

扫一扫