【霍夫变换】图像处理（OpenCV）-part11

最新推荐文章于 2025-04-26 18:37:55 发布

绝顶大聪明

最新推荐文章于 2025-04-26 18:37:55 发布

阅读量815

点赞数 26

文章标签：图像处理 opencv 人工智能

本文链接：https://blog.csdn.net/2302_77326347/article/details/147489705

版权

20 霍夫变换

20.1 理解霍夫变换

霍夫变换的基本思想是将图像空间中的几何元素（如直线、圆等）通过参数方程转换到参数空间中，形成一个参数空间的累加器数组。图像空间中的每个点在参数空间中对应一个曲线或曲面，而几何形状在图像空间中的对应关系则表现为参数空间中的曲线或曲面的交点。通过在参数空间中寻找累加器数组的局部极大值，可以确定这些几何形状的参数，从而实现对图像中相应形状的检测。

霍夫变换是图像处理的一种技术，主要用于检测图像中的直线、圆等几何形状。基本思想就是将图像空间中的点映射到参数空间中，通过在参数空间中寻找累计最大值实现对特定形状的检测。

20.2 霍夫直线变换

对于一条直线（不垂直于x轴的直线），都可以用y=k x+q来表示，此时，x和y是横纵坐标，k和q是一个固定参数。当我们换一种方式来看待这个式子，我们就可以得到：

q = -kx + y

此时，以k和q为横纵坐标，x和y为固定参数，也就是说k和q成了自变量和因变量，变换如下图所示：

从上图可以看出，在直角坐标系下的一个直线，在变换后的空间中仅仅表示为一点，对于变换后的空间，我们称其为霍夫空间，也就是参数空间。也就是说，直角坐标系下的一条直线对应了霍夫空间中的一个点。类似的，霍夫空间中的一条直线也对应了直角坐标系中的一个点，如下图所示：

那么对于一个二值化后的图形来说，其中的每一个目标像素点（这里假设目标像素点为白色像素点）都对应了霍夫空间的一条直线，当霍夫空间中有两条直线相交时，就代表了直角坐标系中某两个点所构成的直线。而当霍夫空间中有很多条线相交于一点时，说明直角坐标系中有很多点能构成一条直线，也就意味着这些点共线，因此我们就可以通过检测霍夫空间中有最多直线相交的交点来找到直角坐标系中的直线。

基本对应关系

直线与点：在直角坐标系中，直线 y=ax+b，参数空间用 a（斜率）和 b（截距）表示直线，所以直角坐标系的一条直线对应参数空间的一个点 (a,b)。

点与直线：在直角坐标系中，一个点 (x0,y0)，代入直线方程得 y0=ax0+b，变形为 b=y0−ax0，这在参数空间是一条直线。参数空间的这条直线代表所有可能经过直角坐标系点 (x0,y0) 的直线的参数组合。

直角坐标系与霍夫空间的联系

两直线相交：直角坐标系中的两个点 (x1,y1) 和 (x2,y2)，它们在参数空间分别对应直线 b=y1−ax1 和 b=y2−ax2。联立解方程，可得交点 (a′,b′)。此交点即所求直线的参数，对应直角坐标系中两点连成的直线方程 y=a′x+b′。

多线相交于一点：若有多个点共线，这些点在直角坐标系的直线方程为 y=a0x+b0。在参数空间，每个共线点对应的直线都经过 (a0,b0)，多条直线交于一点，说明直角坐标系的多个点共线，参数空间交点即共线直线参数。

参数坐标系中，相交在一点的直线越多，说明在直角坐标系中，有越多的点构成直线

总结

参数空间中，相交在一点的直线越多，说明在直角坐标系中，有越多的点构成直线。

累加器值表示有多少个点共线。

通过寻找参数空间中累加器值的局部极大值，可以检测出直角坐标系中的直线。

然而对于x=1这种直线（垂直于x轴）来说，y已经不存在了，斜率无穷大，无法映射到霍夫空间中去，那么就没办法使用上面的方法进行检测了，为了解决这个问题，我们就将直角坐标系转化为极坐标系，然后通过极坐标系与霍夫空间进行相互转化。

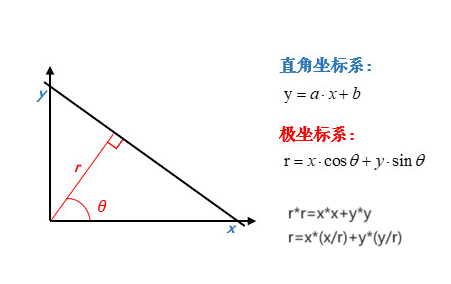
在极坐标系下是一样的，极坐标中的点对于霍夫空间中的线，霍夫空间中的点对应极坐标中的直线。并且此时的霍夫空间不再是以k为横轴、b为纵轴，而是以为θ横轴、ρ(上图中的r)为纵轴。上面的公式中，x、y是直线上某点的横纵坐标（直角坐标系下的横纵坐标），和是极坐标下的坐标，因此我们只要知道某点的x和y的坐标，就可以得到一个关于θ-ρ的表达式，如下图所示：

根据上图，霍夫空间在极坐标系下，一点可以产生一条三角函数曲线，而多条这样的曲线可能会相交于同一点。因此，我们可以通过设定一个阈值，来检测霍夫空间中的三角函数曲线相交的次数。如果一个交点的三角函数曲线相交次数超过阈值，那么这个交点所代表的直线就可能是我们寻找的目标直线。

使用API

lines=cv2.HoughLines(image, rho, theta, threshold)

image：输入图像，通常为二值图像，其中白点表示边缘点，黑点为背景。

rho：r的精度，以像素为单位，表示霍夫空间中每一步的距离增量, 值越大，考虑越多的线。

theta：角度θ的精度，通常以弧度为单位，表示霍夫空间中每一步的角度增量。值越小，考虑越多的线。

threshold：累加数阈值，只有累积投票数超过这个阈值的候选直线才会被返回。

返回值：cv2.HoughLines 函数返回一个二维数组，每一行代表一条直线在霍夫空间中的参数 (rho, theta)。

import cv2 as cv
import numpy as np
img = cv.imread("images/huofu.png")
#灰度转换
img_gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
#边缘检测
img_edge = cv.Canny(img_gray, 30, 70)
#霍夫直线变换
lines = cv.HoughLines(img_edge, 0.8, np.pi/180, 90)
for line in lines:
    rho,theta = line[0]
    sin_theta = np.sin(theta)
    cos_theta = np.cos(theta)
    x1,x2 = 0,img_edge.shape[1]
    y1,y2 = int((rho -x1 * cos_theta)/sin_theta),int((rho -x2 * cos_theta)/sin_theta)
    cv.line(img, (x1,y1), (x2,y2), (100,100,255), 1)
cv.imshow("img", img)
cv.waitKey()
cv.destroyAllWindows()

20.3 统计概率霍夫直线变换

前面的方法又称为标准霍夫变换，它会计算图像中的每一个点，计算量比较大，另外它得到的是整一条线（r和θ），并不知道原图中直线的端点。所以提出了统计概率霍夫直线变换(Probabilistic Hough Transform)，是一种改进的霍夫变换，它在获取到直线之后，会检测原图中在该直线上的点，并获取到两侧的端点坐标，然后通过两个点的坐标来计算该直线的长度，通过直线长度与最短长度阈值的比较来决定该直线要不要被保留。

使用API

lines=cv2.HoughLinesP(image, rho, theta, threshold, lines=None, minLineLength=0, maxLineGap=0)

image：输入图像，通常为二值图像，其中白点表示边缘点，黑点为背景。

rho：极径分辨率，以像素为单位，表示极坐标系中的距离分辨率。

theta：极角分辨率，以弧度为单位，表示极坐标系中角度的分辨率。

threshold：阈值，用于过滤掉弱检测结果，只有累计投票数超过这个阈值的直线才会被返回。

lines（可选）：一个可初始化的输出数组，用于存储检测到的直线参数。

minLineLength（可选）：最短长度阈值，比这个长度短的线会被排除。

maxLineGap（可选）：同一直线两点之间的最大距离。当霍夫变换检测到一系列接近直角的线段时，这些线段可能是同一直线的不同部分。maxLineGap参数指定了在考虑这些线段属于同一直线时，它们之间最大可接受的像素间隔。

返回值lines：cv2.HoughLinesP 函数返回一个二维数组，每个元素是一个包含4个元素的数组，分别表示每条直线的起始点和结束点在图像中的坐标（x1, y1, x2, y2）。

def func2():
    # 读取图像
    img = cv.imread("images/huofu.png")
    if img is None:
        print("无法加载图像，请检查文件路径是否正确。")
        return

    # 灰度转换
    img_gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)

    # 边缘检测
    img_edge = cv.Canny(img_gray, 30, 70)

    # 霍夫直线变换
    lines = cv.HoughLinesP(img_edge, 1, np.pi/180, 100, minLineLength=100, maxLineGap=10)
    # 遍历所有检测到的直线
    for line in lines:
        x1, y1, x2, y2 = line[0]
        cv.line(img, (x1, y1), (x2, y2), (100, 200, 200), 2)
    # 显示结果
    cv.imshow("img", img)
    cv.waitKey()
    cv.destroyAllWindows()

func2()

20.4 霍夫圆变换

霍夫圆变换跟直线变换类似，它可以从图像中找出潜在的圆形结构，并返回它们的中心坐标和半径。只不过线是用(r,θ)表示，圆是用(x_center,y_center,r)来表示，从二维变成了三维，数据量变大了很多；所以一般使用霍夫梯度法减少计算量。

使用API

circles=cv2.HoughCircles(image, method, dp, minDist, param1, param2)

image：输入图像，通常是灰度图像。

method：使用的霍夫变换方法:霍夫梯度法，可以是 cv2.HOUGH_GRADIENT，这是唯一在OpenCV中用于圆检测的方法。

dp：累加器分辨率与输入图像分辨率之间的降采样比率，用于加速运算但不影响准确性。设置为1表示霍夫梯度法中累加器图像的分辨率与原图一致

minDist：检测到的圆心之间的最小允许距离，以像素为单位。在霍夫变换检测圆的过程中，可能会检测到许多潜在的圆心。minDist 参数就是为了过滤掉过于接近的圆检测结果，避免检测结果过于密集。当你设置一个较小的 minDist 值时，算法会尝试找出尽可能多的圆，即使是彼此靠得很近的圆也可能都被检测出来。相反，当你设置一个较大的 minDist 值时，算法会倾向于只检测那些彼此间存在一定距离的独立的圆。

param1 和 param2：这两个参数是在使用 cv2.HOUGH_GRADIENT 方法时的特定参数，分别为：

param1(可选)：阈值1，决定边缘强度的阈值。

param2：阈值2，控制圆心识别的精确度。较大的该值会使得检测更严格的圆。param2 通常被称为圆心累积概率的阈值。在使用霍夫梯度方法时，param2 设置的是累加器阈值，它决定了哪些候选圆点集合被认为是有效的圆。较高的 param2 值意味着对圆的检测更严格，只有在累加器中积累了足够高的响应值才认为是真实的圆；较低的 param2 值则会降低检测的门槛，可能会检测到更多潜在的圆，但也可能包含更多的误检结果。

返回值：cv2.HoughCircles 返回一个二维numpy数组，包含了所有满足条件的圆的参数。

def func3():
    # 读取图像
    img = cv.imread("images/huofu.png")
    if img is None:
        print("无法加载图像，请检查文件路径是否正确。")
        return

    # 灰度转换
    img_gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)

    # 边缘检测
    img_edge= cv.Canny(img_gray, 30, 70)
    # 霍夫圆变换
    circles = cv.HoughCircles(img_edge, cv.HOUGH_GRADIENT, 1, 20, param1=50, param2=30, minRadius=0, maxRadius=0)
    if circles is not None:
        circles = np.uint16(np.around(circles))
        print(circles)
        for circle in circles[0, :]:
            x, y, r = circle
            cv.circle(img, (x, y), r, (100, 200, 255), 2)
    # 显示结果
    cv.imshow("img", img)
    cv.waitKey()
    cv.destroyAllWindows()

func3()