引言:
线段树和树状数组,是两个十分相似的数据结构。他们能使对一个区间的数修改以及查询的速度提升许多。两个结构本质相同,各有优缺点,今天我们来从单点修改,单点查询,区间修改,区间查询。
线段树和树状数组的区别
线段树可以在O(log(N))时间复杂度内寻找区间极值和区间和,线段树的创建时间复杂度为O(log(N)),空间复杂度为O(>=2n-1);树状数组可以在O(log(N))的时间复杂度内计算区间极值和区间和,树状数组的创建时间复杂度为O(Nlog(N)),空间复杂度为O(N)。线段树求解的区间是任意的,越界也无所谓,但是树状数组求解的区间必须是从1开始的合法区间
线段树:
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。
比如讲一个有4个数的线段树,是长这个样子的:

一号节点,代表着区间1~4
二号节点,代表区间1~2
三号节点,代表区间3~4
以此类推。。。。。。
很容易发现,对于n号节点来说,n×2代表着它的区间的前半段,n×2+1代表着它的区间的后半段。
树状数组:
前置知识:Lowbit() 非负整数n在二进制表示下最低位1及其后面的0构成的数值。
这里有一个很关键的东西,叫做lowbit,lowbit是将一个二进制数的所有高位一都去掉,只留下最低位的1,比如lowbit(5)=lowbit(0101(二进制))=0001(二进制)
x & - x(二进制转变)
规则:这里是tree数组的相加(),只有偶数才有变化,奇数为本身!!!
(数值)二进制:=?(这里假设main函数输入用的数组名是input)
(1)1=1 tree[1]=input[1];
(2) 10=10+1 tree[2]=input[2]+tree[1];
(3) 11=11 tree[3]=input[3];
(4) 100=100+11+10 tree[4]=input[4]+tree[3]+tree[2];
(6) 110=110+101 tree[6]=input[6]+tree[5];
(8) 1000=1000+111+110+100 tree[8]=input[8]+tree[7]+tree[6]+tree[4];
(10)1010=1010+1001; tree[10]=input[10]+tree[9];
(12) 1100=1100+1011+1010 tree[12]=input[12]+tree[11]+tree[10];
(14) 1110=1110+1101; tree[14]=input[14]+tree[13];
如下图,如下下图

tree[x]保存以为根的子树中叶节点值的和
tree[x]节点的长度等于lowbit(x)
tree[x]节点的父节点为t[x+lowbit(x)]
整棵树的深度为log2n +1
树状数组是一个很奇特的树,它的节点会比线段树少一些,也能表示一个数组。
比如一个数组叫做a有8个数,那么它的树状数组样子就长这样c数组就是树状数组,能看出来
c1=a1; c2=a1+a2; c3=a3; c4=a1+a2+a3+a4;
以此类推。。。。。。 很难说出他们的关系,但是如果把它们变为二进制
c0001=a0001 c0010=a0001+a0010 c0011=a0011 c0100=a0001+a0010+a0011+a0100
你会发现,将每一个二进制,去掉所有高位1,只留下最低位的1,然后从那个数一直加到1,看一看是不是这样。

线段树构造
因为树状数组不需要构造这一过程,所以先讲线段树的构造
就是用到递归:先设left=1,right=n,然后每一次递归,left、mid和mid+1、right。代码如下:
void build(int left,int right,int index)
{
tree[index].left=left;
tree[index].right=right;
if(left==right)
return ;
int mid=(right+left)/2;
build(left,mid,index*2);
build(mid+1,right,index*2+1);
}线段树单点修改
单点修改就是每到一个节点,看这个节点代表着的区间包括不包括这个点,包括就加上。
void my_plus(int index,int dis,int k)
{
tree[index].num+=k;
if(tree[index].left==tree[index].right)
return ;
if(dis<=tree[index*2].right)
my_plus(index*2,dis,k);
if(dis>=tree[index*2+1].left)
my_plus(index*2+1,dis,k);
}树状数组单点修改
也叫做树状数组的维护
void add(int x,int k)
{
while(x<=n)
{
tree[x]+=k;
x+=lowbit(x);
}
}线段树区间查询
区间查询就是,每查到一个区间,有三种选择:
1、如果这个区间被完全包括在目标区间内,那么加上这个区间的和,然后return;
2、如果这个区间的right>目标区间的left,那么查询这个区间;
3、如果这个区间的left<目标区间的right,也查询这个区间;
void search(int index,int l,int r)
{
if(tree[index].left>=l && tree[index].right<=r)
{
ans+=tree[index].num;
return ;
}
if(tree[index*2].right>=l)
search(index*2,l,r);
if(tree[index*2+1].left<=r)
search(index*2+1,l,r);
}树状数组区间查询
就是前缀和,比如查询x到y区间的和,那么就将从1到y的和-从1到x的和。
从1到y的和求法是,将y转为2进制,然后一直减去lowbit(y),一直到0
比如求1到7的和
int sum(int x)
{
int ans=0;
while(x!=0)
{
ans+=tree[x];
x-=lowbit(x);
}
return ans;
}线段树区间修改
和线段树区间查询类似,分为三种
1、如果当前区间完全属于要加的区间,那么这个区间,也就是节点加上,然后return;
2、如果这个区间的right>目标区间的left,那么查询这个区间;
3、如果这个区间的left<目标区间的right,也查询这个区间;
void pls(int index,int l,int r,int k)
{
if(tree[index].left>=l && tree[index].right<=r)
{
tree[index].num+=k;
return ;
}
if(tree[index*2].right>=l)
pls(index*2,l,r,k);
if(tree[index*2+1].left<=r)
pls(index*2+1,l,r,k);
}树状数组区间修改
这就会变的很好玩。如果将x到y区间加上一个k,那就是从x到n都加上一个k,再从y+1到n加上一个-k
但是要修改区间x到区间y是这样用的,z为增减的值
add(x,z); //用到差分的思想,在一个部分加上多少,在到后面一个位置坐截止,就相当于改变了其中间的量
add(y+1,-z);void add(int x,int k)
{
while(x<=n)
{
tree[x]+=k;
x+=lowbit(x);
}
}线段树单点查询
就是从根节点,一直搜索到目标节点,然后一路上都加上就好了。
void search(int index,int dis)
{
ans+=tree[index].num;
if(tree[index].left==tree[index].right)
return ;
if(dis<=tree[index*2].right)
search(index*2,dis);
if(dis>=tree[index*2+1].left)
search(index*2+1,dis);
}树状数组单点查询
从x点,一直x-=lowbit(x),沿途都加上就好啦
int search(int x)
{
int ans=0;
while(x!=0)
{
ans+=tree[x];
x-=lowbit(x);
}
return ans;
}看到这里,相信你现在已经学有所成了,那么来小试牛刀一下吧!!!
实战演练
1.【模板】树状数【模板】树状数组1

输入:
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4注意:只修改一个数(单点修改),却要输出一个区间的值(区间查询)!!!
解法一:线段树
#include<bits/stdc++.h> //线段树
using namespace std;
const int N = 5e5+5;
int n,m,ans;
int he=0;
int input[N];
struct node { //结构体,left,right表示input[left]~input[right]的范围,从left开始,到right结束,tree.num表示他们之间的和
int left,right;
int num;
} tree[2000010];
void build(int left,int right,int index) { //创建线段树
he++;
tree[index].left=left;
tree[index].right=right;
if(left==right)
return ;
int mid=(right+left)/2;
build(left,mid,index*2);
build(mid+1,right,index*2+1);
}
int add(int index) { //输入时候的tree数组,tree[i]=tree[2*i]+tree[2*i+1]
if(tree[index].left==tree[index].right) {
//cout<<index<<" "<<input[tree[index].right]<<endl; //验证
tree[index].num=input[tree[index].right];
return tree[index].num;
}
tree[index].num=add(index*2)+add(index*2+1);
return tree[index].num;
}
void my_plus(int index,int dis,int k) { //区间修改
tree[index].num+=k;
if(tree[index].left==tree[index].right)
return ;
if(dis<=tree[index*2].right)
my_plus(index*2,dis,k);
if(dis>=tree[index*2+1].left)
my_plus(index*2+1,dis,k);
}
void search(int index,int l,int r) { //计算数组input数组l到r的和
//cout<<index<<" ";
if(tree[index].left>=l && tree[index].right<=r) {
ans+=tree[index].num;
return ;
}
if(tree[index*2].right>=l)
search(index*2,l,r);
if(tree[index*2+1].left<=r)
search(index*2+1,l,r);
}
int main() {
cin>>n>>m;
for(int i=1; i<=n; i++)
cin>>input[i];
build(1,n,1);
add(1);
for(int i=1; i<=m; i++) {
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
if(a==1) {
my_plus(1,b,c);
} else {
ans=0;
search(1,b,c);
printf("%d\n",ans);
}
}
return 0;
}解法二:树状数组
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
int n,m,tree[N];
int lowbit(int k) { //树与二进制的关系
return k & -k;
}
void add(int x,int k) { //关于二进制的树,从子到根
while(x<=n) {
tree[x]+=k;
x+=lowbit(x);
}
}
int sum(int x) { //单点改变,从根到子节点
int ans=0;
while(x!=0) {
ans+=tree[x];
x-=lowbit(x);
}
return ans;
}
int main() {
cin>>n>>m;
for(int i=1; i<=n; i++) {
int a;
cin>>a;
add(i,a);
}
for(int i=1; i<=m; i++) {
int a,b,c;
cin>>a>>b>>c;
if(a==1)
add(b,c);
else
cout<<sum(c)-sum(b-1)<<endl;
}
return 0;
}2.【模板】树状数组2

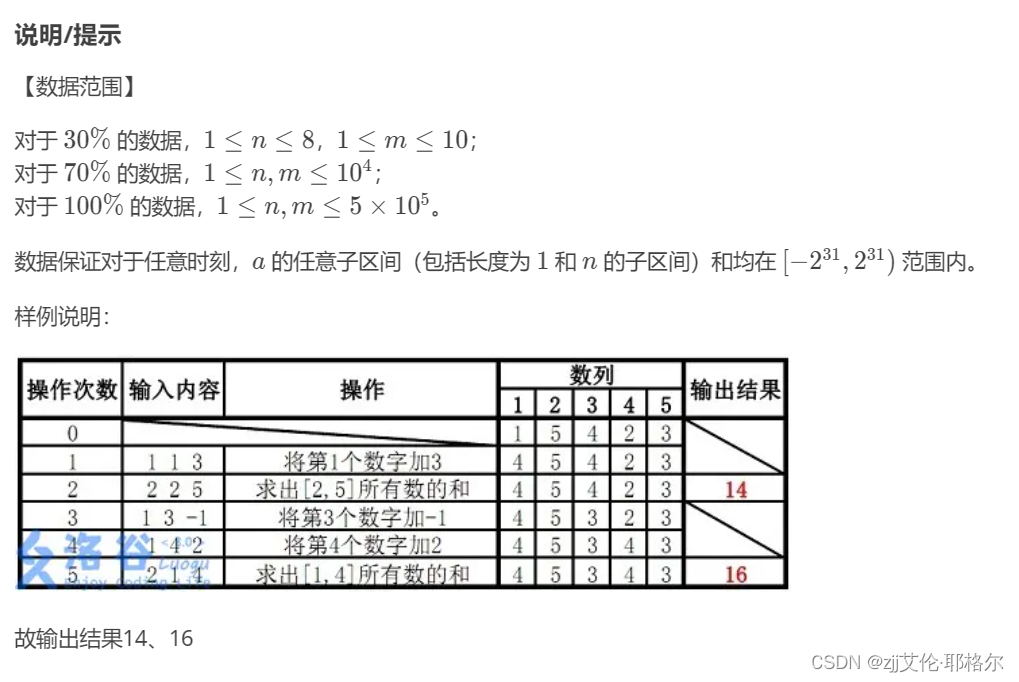
输入:
5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4注意:只修改一个区间(区间修改),却只要输出一个位置的值(单点查询)!!!
方法一:线段树
#include<bits/stdc++.h> //线段树
using namespace std;
int n,m,ans;
const int N=5e5+5;
int input[N];
struct node { //构建线段树需要定义的结构体,他的左支,右支,以及他对应的值
int left,right;
int num;
} tree[4*N];
void build(int left,int right,int index) { //建树从某个点的左右开始,点为index
tree[index].num=0;
tree[index].left=left;
tree[index].right=right;
if(left==right)
return ;
int mid=(right+left)/2; //分治
build(left,mid,index*2);
build(mid+1,right,index*2+1);
}
/*int add(int index) //线段树的单点修改用的上
{
if(tree[index].left==tree[index].right)
{
tree[index].num=input[tree[index].right];
return tree[index].num;
}
tree[index].num=add(index*2)+add(index*2+1);
return tree[index].num;
}
*/
void pls(int index,int l,int r,int k) { //区间修改
if(tree[index].left>=l && tree[index].right<=r) { //如果在指定的范围内,该范围包括左端点和右端点
tree[index].num+=k;
return ;
}
if(tree[index*2].right>=l) //然后将所有涉及到该区间的tree做修改,tree是某给区间前缀和
pls(index*2,l,r,k);
if(tree[index*2+1].left<=r)
pls(index*2+1,l,r,k);
}
void search(int index,int dis) { //用于求第几个数的具体值,一般从1到x开始遍历
ans+=tree[index].num;
if(tree[index].left==tree[index].right)
return ;
if(dis<=tree[index*2].right)
search(index*2,dis);
if(dis>=tree[index*2+1].left)
search(index*2+1,dis);
}
int main() {
int n,m;
cin>>n>>m;
build(1,n,1);
for(int i=1; i<=n; i++)
cin>>input[i];
for(int i=1; i<=m; i++) {
int a;
cin>>a;
if(a==1) {
int x,y,z;
cin>>x>>y>>z;
pls(1,x,y,z);
} else {
ans=0;
int x;
cin>>x;
search(1,x);
printf("%d\n",ans+input[x]);
}
}
return 0;
}注意:只修改一个区间(区间修改),却只要输出一个位置的值(单点查询)!!!
方法二:树状数组
#include<bits/stdc++.h> //树状数组解法
using namespace std;
int n,m;
const int N=5e5+5;
int input[N];
int tree[N];
int lowbit(int x) { //二进制建tree
return x & -x;
}
void add(int x,int k) { //二进制,从子到根节点
while(x<=n) {
tree[x]+=k;
x+=lowbit(x);
}
}
int search(int x) { //单点查询
int ans=0;
while(x!=0) {
ans+=tree[x];
x-=lowbit(x);
}
return ans;
}
int main() {
cin>>n>>m;
for(int i=1; i<=n; i++)
cin>>input[i];
for(int i=1; i<=m; i++) {
int a;
scanf("%d",&a);
if(a==1) {
int x,y,z;
xin>>x>>y>>z;
add(x,z); //用到差分的思想,在一个部分加上多少,在到后面一个位置坐截止,就相当于改变了其中间的量
add(y+1,-z);
} else {
int x;
cin>>x;
printf("%d\n",input[x]+search(x));//值加变化量
}
}
return 0;
}3.【模板】线段树 2

输入:
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4纯纯线段树写法
#include <iostream>
#include <cstdio>
using namespace std;
//题目中给的p
int p;
//暂存数列的数组
long long a[100007];
//线段树结构体,v表示此时的答案,mul表示乘法意义上的lazytag,add是加法意义上的
struct node{
long long v, mul, add;
}st[400007];
//buildtree
void bt(int root, int l, int r){
//初始化lazytag
st[root].mul=1;
st[root].add=0;
if(l==r){
st[root].v=a[l];
}
else{
int m=(l+r)/2;
bt(root*2, l, m);
bt(root*2+1, m+1, r);
st[root].v=st[root*2].v+st[root*2+1].v;
}
st[root].v%=p;
return ;
}
//核心代码,维护lazytag
void pushdown(int root, int l, int r){
int m=(l+r)/2;
//根据我们规定的优先度,儿子的值=此刻儿子的值*爸爸的乘法lazytag+儿子的区间长度*爸爸的加法lazytag
st[root*2].v=(st[root*2].v*st[root].mul+st[root].add*(m-l+1))%p;
st[root*2+1].v=(st[root*2+1].v*st[root].mul+st[root].add*(r-m))%p;
//很好维护的lazytag
st[root*2].mul=(st[root*2].mul*st[root].mul)%p;
st[root*2+1].mul=(st[root*2+1].mul*st[root].mul)%p;
st[root*2].add=(st[root*2].add*st[root].mul+st[root].add)%p;
st[root*2+1].add=(st[root*2+1].add*st[root].mul+st[root].add)%p;
//把父节点的值初始化
st[root].mul=1;
st[root].add=0;
return ;
}
//update1,乘法,stdl此刻区间的左边,stdr此刻区间的右边,l给出的左边,r给出的右边
void ud1(int root, int stdl, int stdr, int l, int r, long long k){
//假如本区间和给出的区间没有交集
if(r<stdl || stdr<l){
return ;
}
//假如给出的区间包含本区间
if(l<=stdl && stdr<=r){
st[root].v=(st[root].v*k)%p;
st[root].mul=(st[root].mul*k)%p;
st[root].add=(st[root].add*k)%p;
return ;
}
//假如给出的区间和本区间有交集,但是也有不交叉的部分
//先传递lazytag
pushdown(root, stdl, stdr);
int m=(stdl+stdr)/2;
ud1(root*2, stdl, m, l, r, k);
ud1(root*2+1, m+1, stdr, l, r, k);
st[root].v=(st[root*2].v+st[root*2+1].v)%p;
return ;
}
//update2,加法,和乘法同理
void ud2(int root, int stdl, int stdr, int l, int r, long long k){
if(r<stdl || stdr<l){
return ;
}
if(l<=stdl && stdr<=r){
st[root].add=(st[root].add+k)%p;
st[root].v=(st[root].v+k*(stdr-stdl+1))%p;
return ;
}
pushdown(root, stdl, stdr);
int m=(stdl+stdr)/2;
ud2(root*2, stdl, m, l, r, k);
ud2(root*2+1, m+1, stdr, l, r, k);
st[root].v=(st[root*2].v+st[root*2+1].v)%p;
return ;
}
//访问,和update一样
long long query(int root, int stdl, int stdr, int l, int r){
if(r<stdl || stdr<l){
return 0;
}
if(l<=stdl && stdr<=r){
return st[root].v;
}
pushdown(root, stdl, stdr);
int m=(stdl+stdr)/2;
return (query(root*2, stdl, m, l, r)+query(root*2+1, m+1, stdr, l, r))%p;
}
int main(){
int n, m;
scanf("%d%d%d", &n, &m, &p);
for(int i=1; i<=n; i++){
scanf("%lld", &a[i]);
}
bt(1, 1, n);
while(m--){
int chk;
scanf("%d", &chk);
int x, y;
long long k;
if(chk==1){
scanf("%d%d%lld", &x, &y, &k);
ud1(1, 1, n, x, y, k);
}
else if(chk==2){
scanf("%d%d%lld", &x, &y, &k);
ud2(1, 1, n, x, y, k);
}
else{
scanf("%d%d", &x, &y);
printf("%lld\n", query(1, 1, n, x, y));
}
}
return 0;
}4.【模板】线段树 1

输入:
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4树状数组写法:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+5;
ll tree1[N];//维护原始数组的差分信息
ll tree2[N];//维护原始数组的(i - 1) * d[i]的差分数组的信息
int n;//原始数组的元素个数
int m;
//临时存放的变量
ll t;
void add(ll tree[], int i, ll v);//在树状数组i位置添加值v
ll sum(ll tree[], int r);//求树状数组[1, r]的累加和
int lowbit(int x);//返回x最右侧的1对应的十进制
void rangeadd(int l, int r, ll v);//让原数组中[l, r]的值都加v
ll range(int l, int r);//返回原数组中[l, r]的累加和
int main() {
cin>>n>>m;//读入原数组中元素的个数和操作的次数
for (int i = 1; i <= n; i++) {//读入原数组中的每个数
cin>>t;
rangeadd(i, i, t);//元素数组中的第i位置相当于在[i, i]区间加一个t
}
for (int i = 0; i < m; i ++) {
cin>>t;
int a,b,c;
if (t == 2) {
cin>>a>>b;
cout<<range(a, b)<<endl;
} else {
cin>>a>>b>>c;
rangeadd(a,b,c);
}
}
return 0;
}
int lowbit(int x) {
return x & -x;
}
void add(ll tree[], int i, ll v) {
while (i <= n) {
tree[i] += v;
i += lowbit(i);
}
}
ll sum(ll tree[], int r) {
ll ans = 0;
while (r) {
ans += tree[r];
r -= lowbit(r);
}
return ans;
}
void rangeadd(int l, int r, ll v) {
//差分操作,在对原数组进行范围的增加
add(tree1, l, v);//在l位置加v
add(tree1, r + 1, -v);//在r + 1位置加-v
//在相同的位置进行操作,只是维护的值不一样,还是一样的树状数组
add(tree2, l, (l - 1) * v);//因为是(i - 1) * d[i]所以是(l - 1) * v;
add(tree2, r + 1, -(r * v));//因为是(i - 1) * d[i]所以是-(r * v)
}
ll range(int l, int r) {
//差分数组中,求原数组的累加和的公式
return r * sum(tree1, r) - sum(tree2, r) - (l - 1) * sum(tree1, l - 1) + sum(tree2, l - 1);
}线段树写法:
线段树要用结构体存储
struct tree{
int l,r;
long long pre,add;
}t[4*maxn+2];建树
在线段树中,从图里也可以看出来,对于一个区间(编号为p),他的左儿子为2p,右儿子为2p+1,so伟大的建树操作就出现了。因为是求修改区间后面区间的值,所以要用
t[p].pre=t[p*2].pre+t[p*2+1].pre;void bulid(int p,int l,int r){
t[p].l=l;t[p].r=r;//以p为编号的节点维护的区间为l到r
if(l==r){//l=r的话,这个区间就只有一个数,直接让区间维护的值等于a[i]
t[p].pre=a[l];
return;
}//否则维护的值等于左儿子加右儿子
int mid=l+r>>1;
bulid(p*2,l,mid);
bulid(p*2+1,mid+1,r);
t[p].pre=t[p*2].pre+t[p*2+1].pre;
} 赖标记
懒标记的精髓就是打标记和下传操作,由于我们要做的操作是区间加一个数,所以我们不妨在区间进行修改时为该区间打上一个标记,就不必再修改他的儿子所维护区间,等到要使用该节点的儿子节点维护的值时,再将懒标记下放即可,可以节省很多时间,对于每次区间修改和查询,将懒标记下传,可以节省很多时间
void spread(int p){
if(t[p].add){//如果懒标记不为0,就将其下传,修改左右儿子维护的值
t[p*2].pre+=t[p].add*(t[p*2].r-t[p*2].l+1);
t[p*2+1].pre+=t[p].add*(t[p*2+1].r-t[p*2+1].l+1);
t[p*2].add+=t[p].add;//为该节点的左右儿子打上标记
t[p*2+1].add+=t[p].add;
t[p].add=0;//下传之后将该节点的懒标记清0
}
}区间修改
考虑将一个区间加上一个数,我们可以从根节点不断向下查找,当发现我们要修改的区间覆盖了当前节点时,我们就把这个区间给修改,并打上懒标记(由于懒标记存在,我们就不必再修改他的儿子节点),否则下传懒标记,继续向下找
void change(int p,int x,int y,int z){
if(x<=t[p].l && y>=t[p].r){//被覆盖的话,就对其进行修改
t[p].pre+=(long long)z*(t[p].r-t[p].l+1);
t[p].add+=z;//打上懒标记
return;
}
spread(p);//如果发现没有被覆盖,那就需要继续向下找,考虑儿子所维护的区间可能因为懒标记的存在而没有修改,因此将懒标记下放
int mid=t[p].l+t[p].r>>1;
if(x<=mid) change(p*2,x,y,z);//如果要修改的区间覆盖了左儿子,就修改左儿子
if(y>mid) change(p*2+1,x,y,z);//右儿子同理
t[p].pre=t[p*2].pre+t[p*2+1].pre;//最终维护的值等于左儿子的值+右儿子的值
}区间查询
考虑询问一个区间的和,依旧是从根节点向下查找,当发现该节点被覆盖时,就返回维护的值,否则下传懒标记,查询左右儿子,累加答案
long long ask(int p,int x,int y){
if(x<=t[p].l && y>=t[p].r) return t[p].pre;//如果被覆盖,就返回维护的值
spread(p);//下传懒标记,并查询左右儿子
int mid=t[p].l+t[p].r>>1;
long long ans=0;
if(x<=mid) ans+=ask(p*2,x,y);
if(y>mid) ans+=ask(p*2+1,x,y);//累加答案,返回左右儿子的和
return ans;
}AC:
#include<bits/stdc++.h>
using namespace std;
const int maxn=100010;
int a[maxn+2];
struct tree{
int l,r;
long long pre,add;
}t[4*maxn+2];
void bulid(int p,int l,int r){
t[p].l=l;t[p].r=r;
if(l==r){
t[p].pre=a[l];
return;
}
int mid=l+r>>1;
bulid(p*2,l,mid);
bulid(p*2+1,mid+1,r);
t[p].pre=t[p*2].pre+t[p*2+1].pre;
}
void spread(int p){
if(t[p].add){
t[p*2].pre+=t[p].add*(t[p*2].r-t[p*2].l+1);
t[p*2+1].pre+=t[p].add*(t[p*2+1].r-t[p*2+1].l+1);
t[p*2].add+=t[p].add;
t[p*2+1].add+=t[p].add;
t[p].add=0;
}
}
void change(int p,int x,int y,int z){
if(x<=t[p].l && y>=t[p].r){
t[p].pre+=(long long)z*(t[p].r-t[p].l+1);
t[p].add+=z;
return;
}
spread(p);
int mid=t[p].l+t[p].r>>1;
if(x<=mid) change(p*2,x,y,z);
if(y>mid) change(p*2+1,x,y,z);
t[p].pre=t[p*2].pre+t[p*2+1].pre;
}
long long ask(int p,int x,int y){
if(x<=t[p].l && y>=t[p].r) return t[p].pre;
spread(p);
int mid=t[p].l+t[p].r>>1;
long long ans=0;
if(x<=mid) ans+=ask(p*2,x,y);
if(y>mid) ans+=ask(p*2+1,x,y);
return ans;
}
int main(){
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
bulid(1,1,n);
for(int i=1;i<=m;i++)
{
int q,x,y,z;
scanf("%d",&q);
if(q==1){
scanf("%d%d%d",&x,&y,&z);
change(1,x,y,z);
}
else {
scanf("%d%d",&x,&y);
cout<<ask(1,x,y)<<endl;
}
}
return 0;
}



















 544
544











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








