胡说八道(24.6.5)—z变换

        上回书说到STM32中的与等于和或等于这两个神奇的符号。

         首先是＂&=＂这个符号。在 STM32 编程中，“与等于”（&=）是一种按位与操作符，用于将一个变量与另一个值进行按位与操作，并将结果赋给该变量。设置特定位：通过将特定的位与 1 进行与等于操作，可以将该位置为 1，而不影响其他位的值。这样就能在特定的为实现置高电平或者是低电平。

        另外一个就是＂ｌ=＂这个符号，其实这两个符号运算差不多。或等于也可以达到设置特定位的操作，不会影响其他的位值。

        还有一张图想和大家分享，就是GPIO引脚的地址是怎么定义的。我们看下图。

        至此，对于简单的stm32引脚定义就差不多了。可以看看简单的代码。

//寄存器版本

GPIOC->BSRR |= (1<<2)|(1<<3);     //GPIOC的2,3置高电平

GPIOA->BSRR |= (1<<4)|(1<<5);     //GPIOA的4,5置高电平

 delay_ms(100);

GPIOC->BSRR |= ((1<<(2+16))|(1<<(3+16)));   //GPIOC的2,3置低电平

GPIOA->BSRR |= ((1<<(4+16))|(1<<(5+16)));   //GPIOA的2,3置低电平

delay_ms(100);

         这只是简单的代码，真正的工程代码可不止这些，包括时钟的配置，库函数的导入等操作这里就不详细介绍了。

        但是，除了这些以外，还遇到了大量的问题。首先，你在Keil4中的仿真，要先勾选一下，魔法棒中Debug部分中的Use Simulator这一个选项。然后，我们编译运行一下，就可以点击“红色的d”按钮进入仿真。仿真是进去了，但是，怎么看引脚的变化呢？点击Peripherals按钮中的General Purpose I/O，就可以找到GPIOA和GPIOC这两组引脚。运行程序，就能看到GPIOC的2，3引脚和GPIOA的4、5引脚在闪烁。

        当然我们也可以通过示波器看看。这里就要滤波器的配置了。

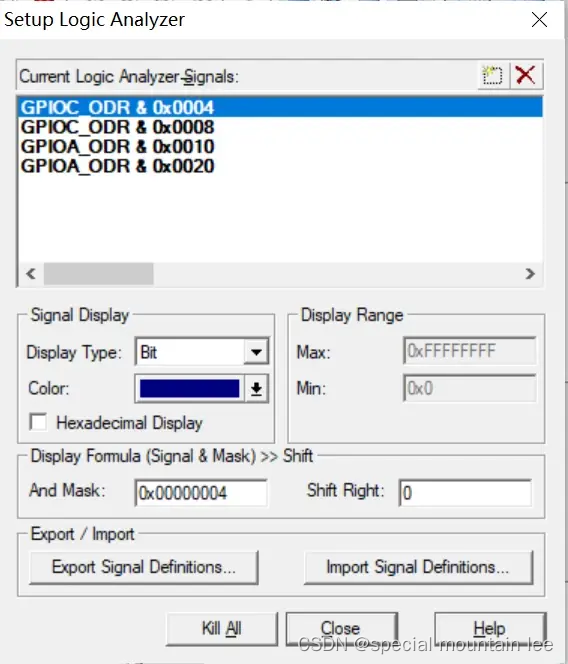
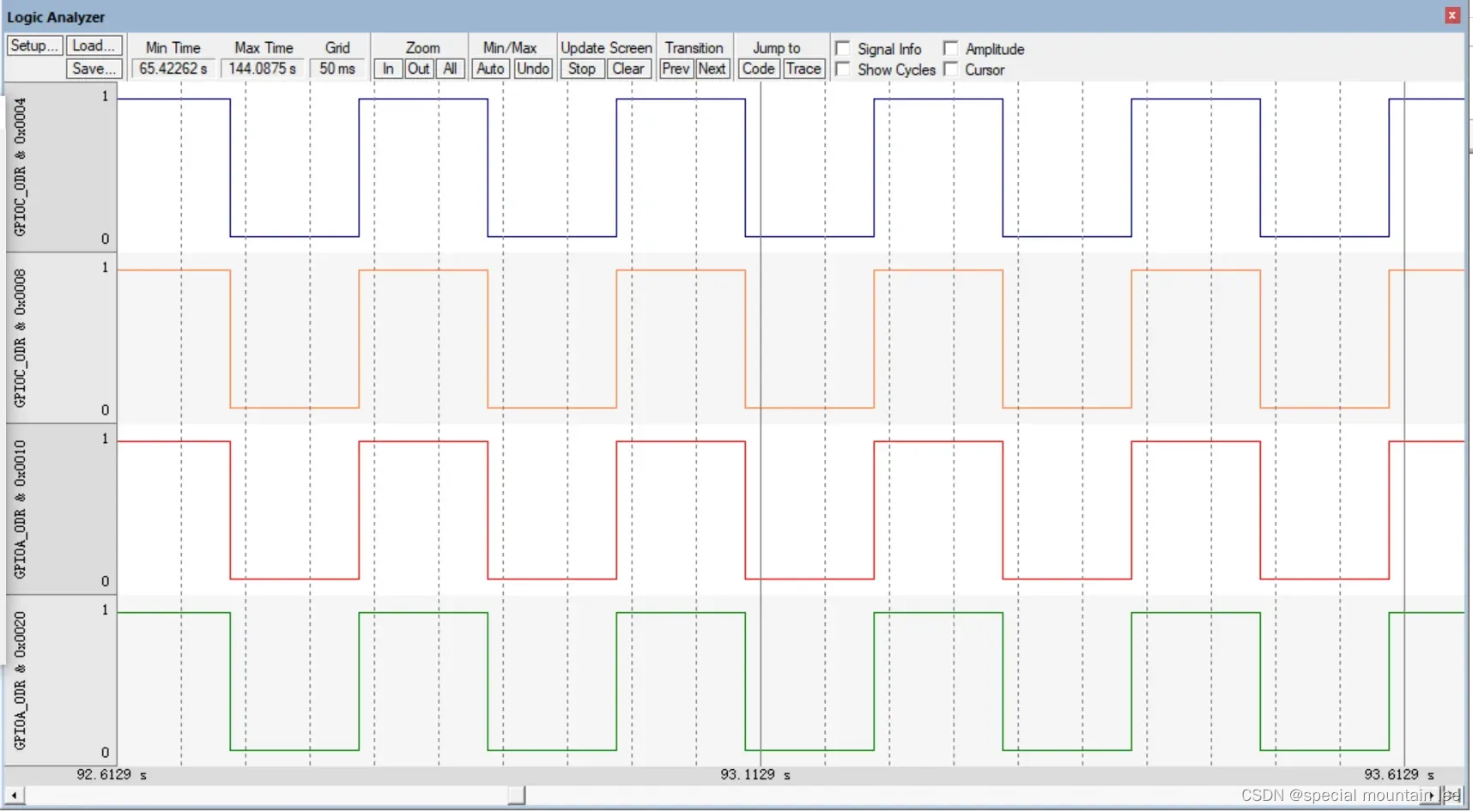
        第一是地址位，前文说到地址位是基地址＆偏移地址。偏移地址我上文已经都给出了。还有一个是Display Type的设置，我们观察的是高低电平，所以要换成bit型。如果你之前都是对的话，应该能看到这样的仿真图。

        现在，咱们进入今天的正题——z变换。大家看看概念。

        ｚ变换就是将离散信号从时域转向复频域的操作。而咱们进行ｚ反变换要求大家回顾一下留数的概念，采用围线积分做。

        另外，之前咱们说ｚ变换是拉普拉斯变换的变种，我们来看看是怎么做到的？它是令z = e＾（st)，具体推导大家可以上网上搜搜。接下来，就是考虑序列的收敛域的问题，不可能所有的信号都能够满足ｚ变换。ｚ变换存在的充分必要条件是级数绝对可和，同时，把使级数绝对可和的成立的所有ｚ值称为ｚ变换域的收敛域。Z变换的收敛域是一个圆环，有时可向内收缩到原点，有时可向外扩展到∞。只有当收敛域是整个Z平面时，Z变换才具有唯一性。

        这里来谈谈这个圆环的由来。看看下图：

        非因果信号的Z变换的收敛域可能包括单位圆外的区域，而因果信号的Z变换的收敛域则必须包括单位圆。这是因为因果信号在时间上是有限的，其Z变换在单位圆上必须收敛，以保证信号的能量有限。

        这里有个疑问，为什么要将信号分成因果信号和非因果信号，只是为了更好地分析和处理信号吗？有知道的请私信或留言。　ＯＵＯ

        ｚ变换的收敛域是因果信号与非因果信号的交集，暂且这么记吧。谈完收敛域，我们来看看ｚ变换的性质。

        首先，不要说肯定是线性。满足齐次性和可加性。

L[x(n)] = X(z),Rx-<|z|<Rx+   L[y(n)] = Y(z),Ry-<|z|<Ry+

L[ax(n)+by(n)] = aX(z)+bY(z),R-<|z|<R+

        第二个是移位操作。

右移：L[x(n-m)] = z^(-m)*X(z)           左移：L[x(n+m)]=z^(m)*X(z)

        第三个是尺度变换。    

L(a^(n)x(n))=X(z/a)

        第四个是线性加权性，就是ｚ域求导数。　

L[nx(n)] = -z*d(X(z))/dz

        第五个是反褶。          

L[x(-n)] = X(1/z)

        第六个是共轭性          

L[x*(n)] = X*(z*)

        第七个是初值定理和终值定理。

        写完了性质，咱们来看看z变换对，上图。

        不知不觉，已经说了这么多了。大家该记记，该背背，舍友压力上号。

        欲知后事如何，且听下回分解。OVO.......