从理论到实践：带你快速学习基于PRM的三种搜索方法

Kita~Ikuyo

已于 2025-04-09 12:52:58 修改

阅读量1.1k

点赞数 28

文章标签： LLM RL python pytorch 人工智能深度学习算法

于 2025-04-06 00:42:01 首次发布

本文链接：https://blog.csdn.net/2303_79071981/article/details/147016903

版权

在开始前，确保您有一些大语言模型(LLM)和强化学习(RL)的基础，如果您没有RL基础我推荐David Sliver的讲座（前三集即可）RL Course by David Silver - Lecture 1: Introduction to Reinforcement Learning - YouTube

叠甲：我对文章中提到的所有算法的数学解析只是片面的，深入研究会在不久的将来发布（也许吧😔），敬请期待😊（欢迎各位大佬指出错误😊）

为什么需要优化扩展测试时计算

LLM的参数规模不断增长，但单纯扩大模型参数面临计算成本高、推理延迟大、缺少数据集等问题。人类在思考难题时往往会倾入更多时间成本，那我们是不是可以将这一现象应用到LLM中呢？幸运的是，在[2408.03314] Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters中，HuggingFace通过实验证明了动态分配计算资源，较小模型可媲美大模型性能(论文中14倍参数差距下的表现)

接下来我将带你从数学理论到编程实践去学习基于验证器的搜索（PRM）的三种搜索算法

数学视角讲解

过程奖励模型(PRM)

数学目标：学习一个函数 $V(s_{t})$ ，预测从中间状态 $s_{t}$ 到最终正确答案的期望回报

关键公式：

1.蒙特卡洛回报计算：

对每个中间步骤 $s_{t}$ ，生成 M 条后续路径 $r_{t}^{(m)}$ = ( $s_{t},a_{t},s_{t+1},...,s_{T}$ )，计算每条路径的最终正确性的得分 $R(\tau _{t}^{(m)})\in \left \{ 0,1 \right \}$

蒙特卡洛估计值：

$V_{MC}(s_{t}) = \frac{1}{M}\sum_{m=1}^{M}R(\tau _{t}^{(m)})$

2.模型训练

PRM参数化为神经网络 $V_{\theta }(s_{t})$ ，优化目标为最小化预测值与蒙特卡洛值的均方误差：

$\mathcal{L}(\theta ) = E_{s_{t}\sim\pi }[(V_{\theta }(s_{t})-V_{MC}(s_{t}))^{2}]$

梯度更新：

$\theta \leftarrow \theta - \alpha \bigtriangledown _{\theta }\mathcal{L}_{\theta }$

均方误差公式：

MSE = $\frac{1}{n}\sum_{i=1}^{n}(y_{i}-\hat{y}_{i})^{2}$

示例：

假设在数学问题 x + 2 = 6 中，中间步骤 $s_{t}$ = " x + 2 "，通过推演后续步骤（如 " x = 6 - 2 " ）的正确性，训练 $V_{\theta }(s_{t})$ 预测该步骤的价值

N选优加权(Best-of-N Weighting)

数学目标：从 N 个候选答案 $\left \{ y_{1},...,y_{N} \right \}$ 中，选择综合评分最高的答案

关键公式：

1.路径评分：

对候选答案 $y_{i}$ ，分解为步骤序列 $\left ( s_{1}^{(i)},...,s_{T}^{(i)} \right )$ ，计算加权得分：

乘积形式： $Score(y_{i})=\prod_{t=1}^{T}V_{\theta }(s_{t}^{(i)})$

或

求和形式： $Score(y_{i})=\sum_{t=1}^{T}V_{\theta }(s_{t}^{(i)})$

2.选择最优答案：

$y^{*} =\arg \underset{1\leq i\leq N}{\max}Score(y_{i})$

示例(这里计算加权得分我们使用乘积形式)：

生成3个候选答案：

$y_{1}$ ：步骤得分[0.6, 0.2]，乘积得分 0.12
$y_{2}$ ：步骤得分[0.3, 0.2]，乘积得分 0.06
$y_{3}$ ：步骤得分[0.1, 0.2]，乘积得分 0.02

选择 $y_{1}$ 作为正确答案

集束搜索(Beam Search)

数学目标：在生成过程中维护 k 条高概率路径，通过动态规划找到全局最优序列

关键公式：

1.路径概率建模：

对生成序列 $y_{1:t} = \left ( w_{1},...,w_{t} \right )$ ，其对数概率为：

$logP_{y_{1:t}} = \sum_{i=1}^{t}logP(w_{i}|w_{1:i-1}, x)$

2.集束维护：

每步扩展所有候选路径，保留前 k 条最高得分路径：

$Beam_{t} = \underset{y_{1:t}}{top\text{-}k}(logP(y_{1:t}))$

3.终止条件：

当所有路径生成结束符或达到最大长度时停止

示例：

在生成方程 2x + 3 = 7 的解时：

路径1：2x = 7 - 3 $\rightarrow$ x = 2（对数概率：-1.2）
路径2：2x = 4 $\rightarrow$ x = 2（对数概率：-0.8）

保留路径2

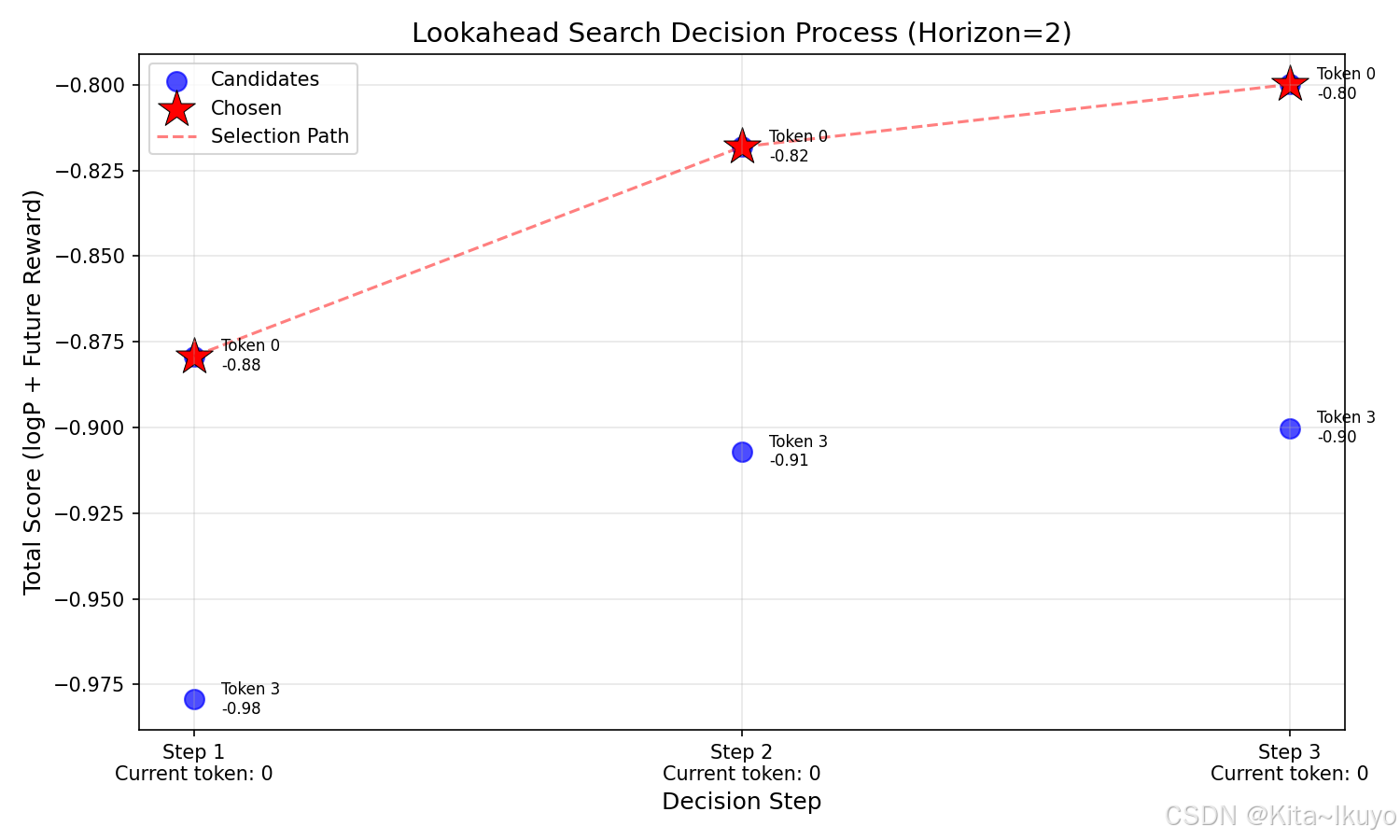
前瞻搜索(Lookahead Search)

数学目标：在当前决策时模拟未来 h 步的可能路径，选择期望回报最高的动作

关键公式

1.未来回报预测：

对当前状态 $s_{t}$ ，生成未来 h 步的路径 $\tau _{t:t+h}$ ，计算预期回报：

$Q(s_{t},a_{t}) = logP(a_{t}|s_{t} )+\gamma \cdot E_{\tau _{t+1:t+h}}[V_{\theta }(s_{t+h})]$

2.动作选择：

$a_{t}^{*} = \arg\underset{a_{t}}{\max}Q(s_{t},a_{t})$

3.值迭代更新：

通过贝尔曼方程更新价值估计：

$V(s_{t})=\underset{a_{t}}{\max}Q(s_{t},a_{t})$

示例：

在解方程时，当前步骤为 2x + 3 = 7，模拟未来两步：

动作1：减去3 $\rightarrow$ 2x = 4 $\rightarrow$ 预测回报 0.9
动作2：除以2 $\rightarrow$ x + 1.5 = 3.5 $\rightarrow$ 预测回报 0.6

选择动作1

如何选择

(出处：原论文第8页）

论文中指出

在简单问题上，N选优加权表现更优；在复杂问题上，集束搜索效率更高
可以通过自适应分配计算预算（如对难题优先使用集束搜索），可减少4倍计算量
在复杂问题的深度优化中，使用前瞻搜索效果更好

总结：

方法	数学核心	计算复杂度	适用场景
Best-of-N	加权评分最大化	O(N⋅T)	简单问题中快速生成多样性答案
集束搜索	动态规划维护top-k路径	O(k⋅T)	复杂问题中平衡质量与效率
前瞻搜索	多步价值预测 + 贝尔曼方程	O( $k^{h}$ )	复杂问题的深度优化

场景匹配指南

任务类型	推荐方法组合
数学/逻辑推理	PRM + Lookahead Search
开放域问答	Best-of-N + 集束搜索
代码生成	PRM + 集束搜索（带语法约束）

代码实现

首先我们定义一个极简的语言模型：

import torch
import torch.nn as nn
import torch.optim as optim

class MiniLM(nn.Module):
    """极简字符级语言模型"""
    def __init__(self, vocab_size=10, hidden_dim=8):
        """
        初始化模型结构
        Args:
            vocab_size: 词汇表大小，默认为10（0-9的数字）
            hidden_dim: LSTM隐藏层维度，默认为8
        """
        super().__init__()
        self.embed = nn.Embedding(vocab_size, hidden_dim)  # 将离散token映射为连续向量
        self.lstm = nn.LSTM(hidden_dim, hidden_dim, batch_first=True)  # LSTM层处理序列
        self.fc = nn.Linear(hidden_dim, vocab_size)  # 输出层预测下一个token的概率分布
    
    def forward(self, x):
        """
        前向传播过程
        Args:
            x: 输入序列，形状为(batch_size, seq_len)
        Returns:
            最后一个时间步的输出，形状为(batch_size, vocab_size)
        """
        x = self.embed(x)         # 转换为嵌入向量 (batch_size, seq_len, hidden_dim)
        out, _ = self.lstm(x)     # LSTM处理序列 (batch_size, seq_len, hidden_dim)
        return self.fc(out[:, -1, :])  # 取最后一个时间步的输出进行预测

    def generate(self, prompt, max_length=1):
        """
        贪心搜索生成序列
        Args:
            prompt: 初始输入序列（例如问题"2+3="的编码）
            max_length: 需要生成的token数量
        Returns:
            生成的最后max_length个token
        """
        current_seq = prompt.tolist()
        for _ in range(max_length):
            input_tensor = torch.tensor(current_seq).unsqueeze(0)  # 添加batch维度
            with torch.no_grad():
                logits = self.forward(input_tensor)  # 获取预测logits
            next_token = torch.argmax(logits, dim=-1).item()  # 选择概率最高的token
            current_seq.append(next_token)
        return current_seq[-max_length:]  # 返回新生成的token

然后定义PRM模型以及训练测试模块：

class PRM(nn.Module):
    """过程奖励模型（Process Reward Model），用于评估中间步骤的质量"""
    def __init__(self, input_dim=8):
        """
        Args:
            input_dim: 输入特征维度，需与语言模型的hidden_dim一致
        """
        super().__init__()
        self.scorer = nn.Sequential(
            nn.Linear(input_dim, 16),  # 将LSTM的隐藏状态映射到更高维空间
            nn.ReLU(),                  # 引入非线性
            nn.Linear(16, 1),           # 降维到单值评分
            nn.Sigmoid()                # 将评分压缩到[0,1]区间
        )
    
    def forward(self, x):
        """输入形状：(batch_size, input_dim)，输出形状：(batch_size, 1)"""
        return self.scorer(x)

def test_prm_training():
    """测试PRM模型的训练过程（使用随机生成的数据）"""
    # 初始化组件
    lm = MiniLM()                       # 语言模型（仅用于结构参考，不参与训练）
    prm = PRM()                         # 待训练的过程奖励模型
    optimizer = optim.Adam(prm.parameters(), lr=0.001)  # 优化器
    
    # 模拟蒙特卡洛推演数据（实际应用中应来自真实推演）
    step_embeddings = torch.randn(100, 8)  # 100个步骤的随机嵌入（形状：100×8）
    mc_returns = torch.rand(100, 1)        # 随机生成模拟回报值（形状：100×1）
    
    # 训练循环
    for epoch in range(10):
        pred = prm(step_embeddings)      # 前向传播获取预测值
        loss = nn.MSELoss()(pred, mc_returns)  # 计算均方误差损失
        optimizer.zero_grad()            # 清空梯度
        loss.backward()                  # 反向传播
        optimizer.step()                 # 更新参数
        print(f"Epoch {epoch}, Loss: {loss.item():.4f}")

然后定义三种搜索算法：

def test_best_of_n(lm, prm):
    """
    Best-of-N采样测试：生成多个候选答案
    Args:
        lm: 训练好的语言模型
        prm: 训练好的过程奖励模型
    """
    # 生成候选答案
    prompt = torch.tensor([2, 0, 3])  # 假设输入序列编码为"2+3="
    candidates = [lm.generate(prompt, max_length=1) for _ in range(5)]  # 生成5个候选答案
    
    # 评分过程
    scores = []
    for cand in candidates:
        # 假设每个候选答案生成过程中有3个步骤（此处用随机嵌入模拟）
        step_embs = torch.randn(3, 8)    # 3个步骤的嵌入（形状：3×8）
        score = prm(step_embs).prod()    # 计算各步骤评分的乘积作为总分
        scores.append(score)
    
    # 选择最高分候选
    best_idx = torch.argmax(torch.stack(scores))
    print(f"Best candidate: {candidates[best_idx]}")


def beam_search(lm, beam_width=2):
    """
    集束搜索实现
    Args:
        lm: 语言模型
        beam_width: 集束宽度（保留的候选序列数量）
    """
    prompt = torch.tensor([2, 0, 3])  # 初始输入序列"2+3="
    sequences = [[list(prompt), 0.0]]  # 格式：[token序列, 对数概率]
    
    for _ in range(3):  # 生成3个token
        new_seqs = []
        for seq, score in sequences:
            # 获取当前序列的下一个token概率
            logits = lm(torch.tensor(seq).unsqueeze(0))
            probs = torch.softmax(logits, dim=-1)
            top_probs, top_tokens = torch.topk(probs, beam_width)  # 取top-k概率
            
            # 扩展候选序列
            for p, t in zip(top_probs[0], top_tokens[0]):
                new_seq = seq + [t.item()]                    # 扩展序列
                new_score = score + torch.log(p).item()       # 累加对数概率
                new_seqs.append((new_seq, new_score))
        
        # 保留得分最高的前beam_width个序列
        sequences = sorted(new_seqs, key=lambda x: -x[1])[:beam_width]
    
    print(f"Beam search result: {sequences[0][0]}")


def lookahead_search(lm, prm, horizon=2):
    """
    前瞻搜索实现：考虑未来多步的潜在奖励
    Args:
        lm: 语言模型
        prm: 过程奖励模型
        horizon: 前瞻步数
    """
    current_seq = [2, 0, 3]  # 初始输入序列"2+3="
    
    for _ in range(3):  # 生成3个token
        candidates = []
        # 获取当前可能的下一个token（取top2）
        logits = lm(torch.tensor(current_seq).unsqueeze(0))
        top_tokens = torch.topk(logits, 2)[1][0]  # 取概率最高的2个token
        
        # 评估每个候选token的未来潜力
        for token in top_tokens:
            temp_seq = current_seq + [token.item()]  # 临时序列
            future_score = 0.0
            
            # 模拟未来horizon步
            for _ in range(horizon):
                next_logits = lm(torch.tensor(temp_seq).unsqueeze(0))
                next_token = torch.argmax(next_logits)  # 贪心选择下一步
                temp_seq.append(next_token.item())
                # 获取该步骤的PRM评分（此处用随机嵌入模拟）
                future_score += prm(torch.randn(1, 8)).item()
            
            # 综合当前token的对数概率和未来评分
            token_prob = torch.softmax(logits, dim=-1)[0, token]
            total_score = torch.log(token_prob).item() + future_score
            candidates.append((token.item(), total_score))
        
        # 选择总分最高的token
        best_token = max(candidates, key=lambda x: x[1])[0]
        current_seq.append(best_token)
    
    print(f"Lookahead result: {current_seq}")

最后就可以愉快运行啦：

if __name__ == "__main__":
    lm = MiniLM()  # 语言模型
    prm = PRM()    # 过程奖励模型
    
    print("==== Testing PRM Training ====")
    test_prm_training()        # 测试PRM训练过程
    
    print("\n==== Testing Best-of-N ====")
    test_best_of_n(lm, prm)    # 测试Best-of-N采样
    
    print("\n==== Testing Beam Search ====")
    beam_search(lm)            # 测试集束搜索
    
    print("\n==== Testing Lookahead Search ====")
    lookahead_search(lm, prm)  # 测试前瞻搜索

样例输出：

==== Testing PRM Training ====
Epoch 0, Loss: 0.0789
Epoch 1, Loss: 0.0787
Epoch 3, Loss: 0.0782
Epoch 4, Loss: 0.0780
Epoch 5, Loss: 0.0777
Epoch 6, Loss: 0.0775
Epoch 7, Loss: 0.0773
Epoch 8, Loss: 0.0771
Epoch 9, Loss: 0.0769

==== Testing Best-of-N ====
Best candidate: [2]

==== Testing Beam Search ====
Beam search result: [tensor(2), tensor(0), tensor(3), 2, 0, 0]

==== Testing Lookahead Search ====
Lookahead result: [2, 0, 3, 2, 0, 0]

为了能更加深刻理解，我添加了可视化数据代码：