电路分析：阻抗和导纳

原创已于 2025-10-23 18:38:40 修改 · 1k 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#电路分析

于 2025-09-17 20:10:19 首次发布

电路分析基础专栏收录该内容

2 篇文章

订阅专栏

对初学者而言，阻抗和导纳是从直流电路（仅有电阻概念）进入到交流电路的关键。也是理解电容电感在电路中的延迟作用的关键。

在上篇文章中，我们讨论了相量的产生背景，他是因为交流电是用三角函数表示的，而三角函数的运算较为复杂，所以利用欧拉公式将三角函数封装成了复数的指数形式，但是他还是有一个旋转因子的干扰，我们再令t=0暂时不管这个旋转因子（因为所有变量的旋转因子都是一样的，最后同乘上即可）。于是得到了一个简单的复数指数，但是复数的指数相加仍然不好算，我们在此利用欧拉公式，把这个复数指数化为复平面上的坐标，最后用极坐标来表示他。最终达到了简化运算的目的。

在最后，我们还推导了电容、电感的VCR的相量形式。本篇文章我们将从这个推导式展开论述。

一、为什么需要阻抗和纳导

在直流电路中，我们只用电阻R和欧姆定律就能描述电流与电压的关系，因为直流电流方向不变，电容会“隔直流、通交流”，电感会“同直流、隔交流”，二者在直流电路中看起来没什么用处。

但到了交流电路（电流 / 电压随时间变化，比如家用 220V 交流电），情况完全不同：

电容会反复 “充电 - 放电”，电感会反复 “储磁 - 释磁”，它们会像电阻一样 “阻碍” 电流，但又不消耗电能（仅储存 / 释放能量）；
此时电流与电压不再 “同相位”（比如电容电流会 “跑在” 电压前面，电感电流会 “落后” 电压），普通电阻无法描述这种 “阻碍 + 相位差” 的综合效果。

因此，我们需要两个新工具：阻抗（Z） 描述 “电路对交流电的总阻碍能力”，导纳（Y） 描述 “电路对交流电的总导通能力”—— 二者本质是 “阻碍” 与 “导通” 的对立概念，就像 “电阻” 和 “电导（G=1/R）” 的关系。

我们可以得出一个结论：阻抗和导纳是交流电中的电阻、电导的对应概念。但是他们又不直接消耗电能发热，只是会对交流电的相位产生阻碍，滞后亦或者是超前。

二、阻抗：交流电路的总阻碍

（1）阻抗的定义

类似于直流电路中，我们让相量的U比上相量的I，就得到了阻抗。这种阻碍不局限于普通电阻对电能的消耗，还包含了电容、电感对相位的偏移。

这里的每个符号都有明确物理意义，新手要先分清 “实部” 和 “虚部”：

实部 R：就是我们熟悉的 “电阻”（单位：欧姆 Ω），代表 “消耗电能的阻碍”（比如电阻器发热），电流与电压同相位（没有时间差）；
虚部 jX：称为 “电抗”（X 是电抗的大小，j 是虚数单位，j²=-1，仅用来表示 “相位差”），代表 “不消耗电能的阻碍”（来自电容或电感），会导致电流与电压产生90° 相位差；
Z：总阻抗（单位：Ω），是 “电阻 + 电抗” 的复数叠加，不是简单的数值相加（比如 R=3Ω、X=4Ω，总阻抗模值是√(3²+4²)=5Ω，不是 3+4=7Ω）。

（2）电抗的两种分身：感抗和容抗

由上一节我们推导的电容相量VCR可知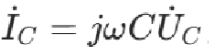：所以电容的电流是超前电压90°的，对于电容的电抗我们称为容抗。相反的，由电感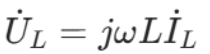可知电感的电压是超前电流90°的，对于电感的电抗我们称为感抗。

我们可以简单记忆：感性元件的电抗会导致电压超前90°；容性元件的电抗会导致电流超前90°。

关键提醒：电抗 X 是容抗和感抗的 “综合效果”—— 如果电路中既有电容又有电感，X = Xl - Xc（因为二者相位相反，会相互抵消）。比如 Xl=5Ω、Xc=3Ω，总电抗 X=2Ω；若 Xl=3Ω、Xc=5Ω，总电抗 X=-2Ω（负号仅代表 “容性主导”，不代表阻碍为负）。这是因为电抗是出现在复平面的概念，而阻抗=实数域电阻值+复数域电抗值。所以在计算阻抗的模值时候可以直接将其放在复平面坐标下，根据矢量的思想求解。

三、导纳：交流电路的总导通

（1）导纳的定义

类似上述阻抗的定义，我们将阻抗取倒数可得到导纳的定义。作用是把 “阻碍” 转化为 “导通”，方便并联电路计算（就像直流电路中 “电导” 比 “电阻” 更适合并联计算）。

因为 Y 是 Z 的倒数（Y=1/Z），所以导纳的复数形式与阻抗 “一一对应”：
Y = G + jB
同样拆解符号：

实部 G：称为 “电导”（单位：西门子 S），是电阻的 “导通能力”，G=1/R（电阻越大，电导越小，导通越弱）；
虚部 jB：称为 “电纳”（B 是电纳的大小），是电抗的 “导通能力”，B=1/X（电抗越大，电纳越小，导通越弱）；
Y：总导纳（单位：S），是 “电导 + 电纳” 的复数叠加，同样遵循复数规则。

（2）电纳的两种分身：容纳和感纳

和电抗对应，电纳也分为 “容纳”（电容的导通能力）和 “感纳”（电感的导通能力），特性同样相反：

关键提醒：电纳 B 是容纳和感纳的 “综合效果”，且符号与电抗相反 ——B = Bc - Bl（因为电抗 X=Xl-Xc，而 B=1/X，所以符号会反转）。比如 Bc=5S、Bl=3S，总电纳 B=2S（容性主导，导通强）；若 Bc=3S、Bl=5S，总电纳 B=-2S（感性主导，导通弱）。

注意：电纳对相位产生的偏移与电抗完全相反，因为电纳本身就是电抗的倒数。当你在使用电纳分析阻碍与导通能力的时候，如果最后得到的是容纳强，则说明容抗弱，进一步推导出感抗强，所以电压相对电流超前90°。相反的如果感纳强，则感抗弱，所以容抗强，所以电流超前电压90°。

电纳对相位的阻碍、导通作用与电抗相反。

四、总结与归纳

（1）电抗、电纳对相位的影响

我们上面推导了电抗与电纳对相位的影响，对此总结一下：

电抗为正的时候，感性强，电压超前；电抗为负的时候，容性强，电流超前。

电纳为正的时候，容性强，电流超前；电纳为负的时候，感性强，电压超前。

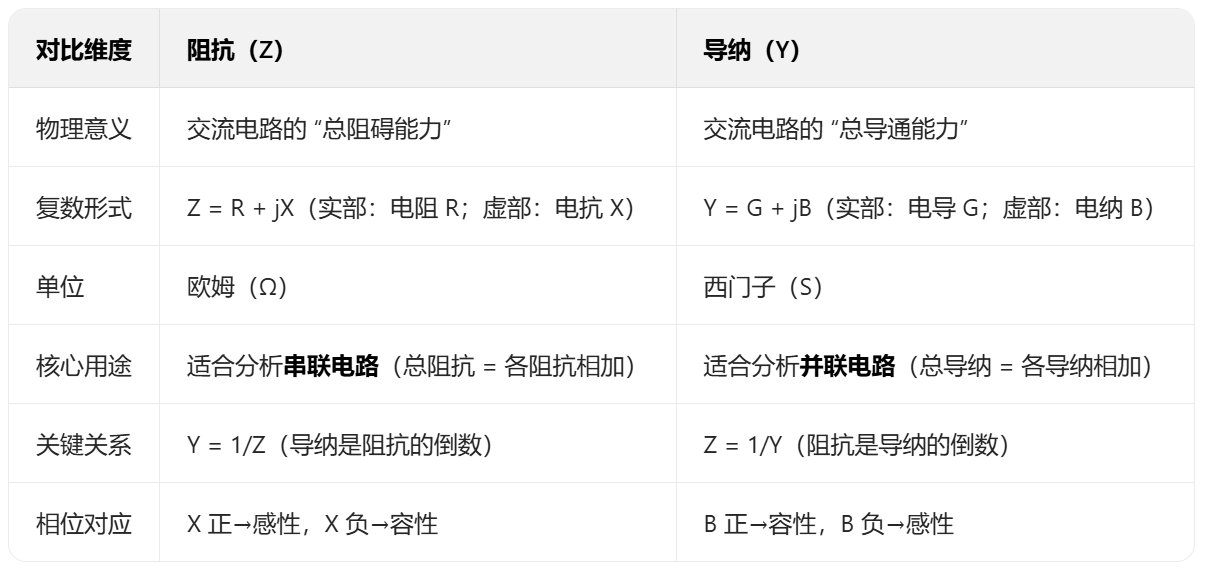
（2）总结

书上最后指出了几点指的我们注意：

（1）阻抗或者导纳是由内部的参数、结构、以及正弦电源的频率决定的。这是从电抗的定义式看出来的，其X=wL或者X=-1/wC；电纳同理。

（2）对于电抗、电纳类似于电阻和电导的关系，都是倒数转换。即由ZY=1。如果包含复数的话，则转化时候分母去模长的平方，实部分子对应不变，虚部分子添加负号。

（3）以前我们学过对电路的串并联技巧都可以用到这里，只需要把电阻替换成阻抗、电导替换成导纳即可，就好像我们对欧姆定律扩展了，把电抗也纳入了电阻分析的的范围