1. 高斯消去法
算法原理:“高斯消去法的基本思想是用逐次消去未知数的方法把原线性方程组化为与其等价的上三角形线性方程组,然后用回代的方法求解上三角形线性方程组。”
算法步骤:a. 输入初始数据(系数矩阵A,右端向量b)
记原方程组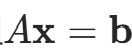 为
为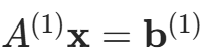 ,其中
,其中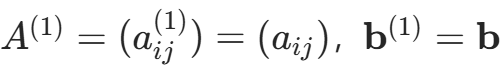 ;
;
b. 第k步消元(k=1,2,⋯,n−1)
若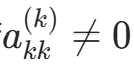 ,则有
,则有
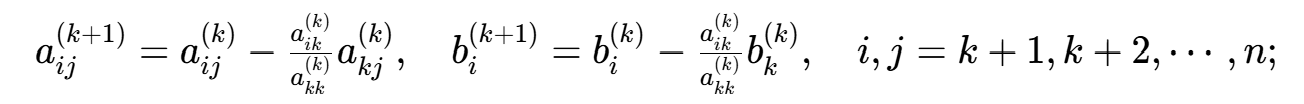
c.若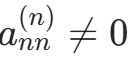 ,则回代
,则回代
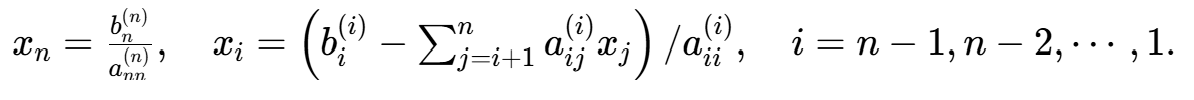
MATLAB 程序:
function x = gauss(A,b)
% A为方程组的系数矩阵,b为方程组的右端向量,x为方程组的解
[m,n] = size(A);
if m ~= n
disp('系数矩阵非方阵'); return;
elseif m ~= length(b)
disp('系数矩阵和右端不匹配'); return;
end
Ab = [A b];
for k = 1:n-1 % 消元过程
if Ab(k,k) == 0
disp('index = 0'); return
end
Ab(k+1:n,k) = Ab(k+1:n,k)/Ab(k,k);
Ab(k+1:n,k+1:end) = Ab(k+1:n,k+1:end) - Ab(k+1:n,k) * Ab(k,k+1:end);
end
if Ab(n,n) == 0
disp('index = 0'); return % 回代过程
end
x(n) = Ab(n,n+1)/Ab(n,n);
for j = n-1:-1:1
x(j) = (Ab(j,n+1) - Ab(j,j+1:n) * x(j+1:n)')/Ab(j,j);
end
数值实验
例 1 用高斯消去法解方程组
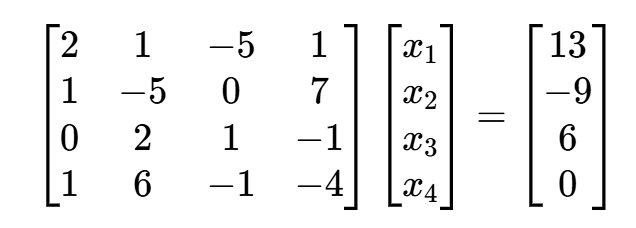
>> A = [2 1 -5 1;1 -5 0 7;0 2 1 -1;1 6 -1 -4];
>> b = [13, -9,6,0]';
>> x = gauss(A,b)
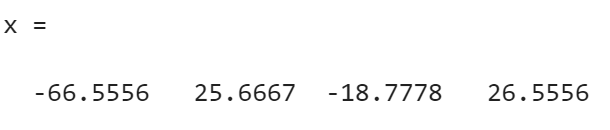
2. 高斯列主元消去法
算法原理:“在采用高斯消去法解线性方程组时,如果主对角元为零或主对角元较小,计算将无法进行或将产生较大误差,故在第k步消元之前,选择系数矩阵第k列主对角线及其以下元素中绝对值最大者作为主元素,并将主元素所在行与第k行对调,然后进行第k步消元。”
算法步骤:
a. 输入初始数据(系数矩阵A,右端向量b);
b. 对k=1,2,⋯,n−1,按列选主元素: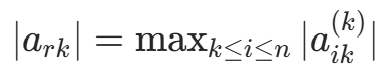 ,如果
,如果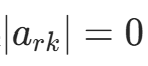 ,则停止计算,否则若
,则停止计算,否则若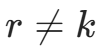 ,则
,则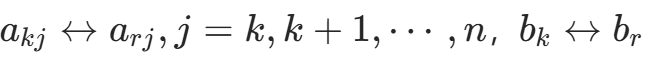 ;
;
c. 第k步消元
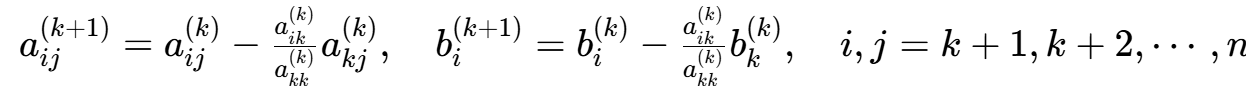
d. 如果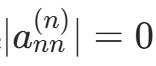 ,则停止计算,否则回代
,则停止计算,否则回代
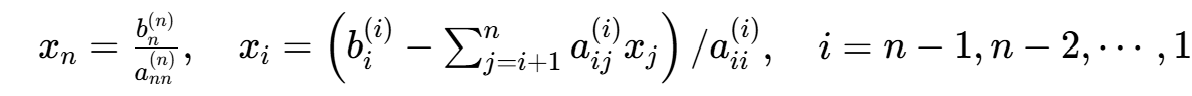
MATLAB 程序:
function [x,P,det] = gaussSys(A,b)
% A为方程组的系数矩阵,b为方程组的右端向量,x为方程组的解
% det为系数矩阵行列式,P为行交换矩阵
[m,n] = size(A);
% 强制将b转为列向量(避免因b是行向量导致的维度错误)
b = b(:);
if m ~= n
disp('系数矩阵非方阵'); return;
elseif m ~= length(b)
disp('系数矩阵和右端向量不匹配'); return;
end
Ab = [A b]; % 构造增广矩阵(此时b已确保为列向量,Ab维度为n×(n+1))
det = 1;
x = zeros(n,1); % x是列向量,每个x(k)是标量
P = eye(n);
for k = 1:n-1 % 消元过程
[amax,imax] = max(abs(Ab(k:n,k)));
if amax == 0
disp('方程组奇异'); det = 0; return;
elseif k ~= imax + k - 1
% 交换行(确保主元在对角线上)
P([k, imax + k - 1], :) = P([imax + k - 1, k], :);
Ab([k, imax + k - 1], :) = Ab([imax + k - 1, k], :);
end
% 计算消元因子并更新增广矩阵
Ab(k+1:n,k) = Ab(k+1:n,k)/Ab(k,k);
Ab(k+1:n,k+1:end) = Ab(k+1:n,k+1:end) - Ab(k+1:n,k) * Ab(k,k+1:end);
det = Ab(k,k) * det; % 累乘主元计算行列式
end
% 检查最后一个主元是否为0(方程组奇异)
if Ab(n,n) == 0
disp('方程组奇异'); det = 0; return;
end
det = Ab(n,n) * det; % 完成行列式计算
% 回代求解(用矩阵乘法实现点积,确保结果为标量)
x(n) = Ab(n,n+1)/Ab(n,n); % 最后一个未知数
for k = n-1:-1:1
% 行向量Ab(k,k+1:n)与列向量x(k+1:n)的矩阵乘法(点积),结果为标量
x(k) = (Ab(k,n+1) - Ab(k,k+1:n) * x(k+1:n))/Ab(k,k);
end
end
数值实验
例 2 用高斯列主元消去法解方程组
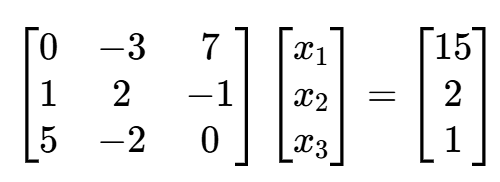
>> A = [0 -3 7;1 2 -1;5 -2 0];
>> b = [15,2,1]';
>> [x,P,det] = gaussSys(A,b)

例 3 线性方程组Ax=b的A和b分别为
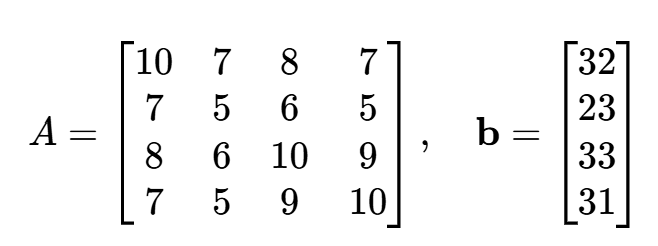
则解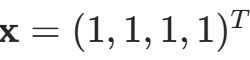 。用 MATLAB 内部函数求detA及A的所有特征值和
。用 MATLAB 内部函数求detA及A的所有特征值和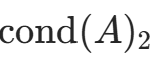 。
。
若令
求解(A+δA)(x+δx)=b,输出向量δx和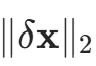 。从理论结果和实际计算两方面分析线性方程组Ax=b解的相对误差
。从理论结果和实际计算两方面分析线性方程组Ax=b解的相对误差![]() 及A的相对误差
及A的相对误差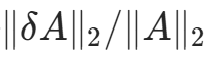 的关系。
的关系。
>> A = [10,7,8,7;7,5,6,5;8,6,10,9;7,5,9,10];
>> b = [32,23,33,31]';
>> [x,P,det] = gaussSys(A,b)

>> eig(A)

>> cond(A)

从系数矩阵条件数可以看出Ax=b为病态方程组。接下来考虑方程组(A+δA)(x+δx)=b解的情况。
>> AA = [10,7,8.1,7.2;7.08,5.04,6,5;8,5.98,9.89,9;6.99,5,9,9.98];
>> [xx,P,det] = gaussSys(AA,b)

>> dx = xx - x
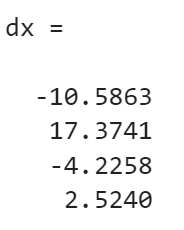
>> norm(dx)

>> dA = AA - A

>> norm(dA)

>> norm(dx)/norm(x)

>> norm(dA)/norm(A)

>> 10.4661/0.0076

从计算结果可以看出,系数矩阵的相对误差仅为0.0076,但解的相对误差达到了10.4661,系数矩阵的微小变化引起了解的很大变化,原因就在于该方程组的系数矩阵为病态矩阵,条件数约为2984。
3. 矩阵直接三角分解法
算法原理:“将高斯消去法改写为紧凑格式,直接从矩阵A的元素得到计算L,U元素的计算公式,从而得到A的LU分解。实现了矩阵A的LU分解,求解Ax=b的问题就等价于求解两个三角形方程组:求解Ly=b,得y;求解Ux=y,得x。”
算法步骤:设A的所有顺序主子式都不为零。
① 计算U的第 1 行,L的第一列:
![]()
② 计算U的第r行,L的第r列元素(r=2,3,⋯,n):
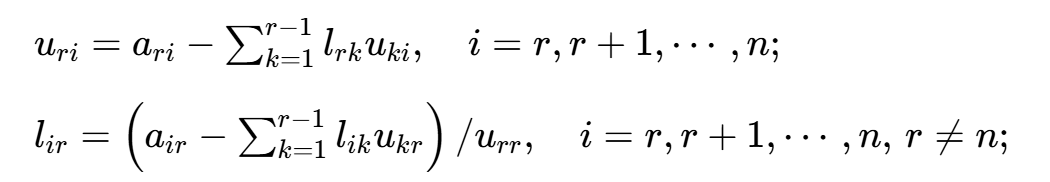
③ 求解Ly=b:
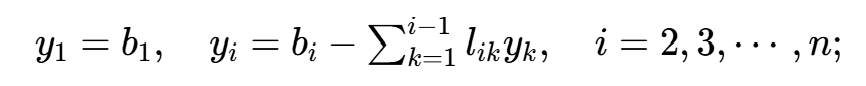
④ 求解Ux=y:
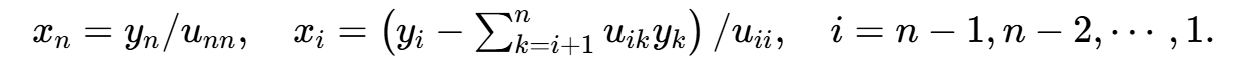
MATLAB 程序:
function [L,U,y,x] = Doolittle(A,b)
% A为系数矩阵,b为方程组右端
% x为方程组Ax = b的解,y为方程组Ly = b的解
% L为单位下三角阵,U为上三角阵
[m,n] = size(A);
if m ~= n
disp('系数矩阵非方阵'); return;
end
L = eye(n,n); U = zeros(n,n);
U(1,1:n) = A(1,1:n); L(1:n,1) = A(1:n,1)/U(1,1);
for k = 2:n
U(k,k:n) = A(k,k:n) - L(k,1:(k-1)) * U(1:(k-1),k:n);
if U(k,k) == 0
disp('方程组奇异'); return;
end
L((k+1):n,k) = (A((k+1):n,k) - L((k+1):n,1:(k-1)) * U(1:(k-1),k))/U(k,k);
end
if U(n,n) == 0
disp('方程组奇异'); return;
end
y(1) = b(1);
for k = 2:n
y(k) = b(k) - L(k,1:k-1) * y(1:k-1)';
end
x(n) = y(n)/U(n,n);
for k = n-1:-1:1
x(k) = (y(k) - U(k,k+1:n) * x(k+1:n)')/U(k,k);
end
数值实验
例 4 用矩阵直接三角分解法解方程组
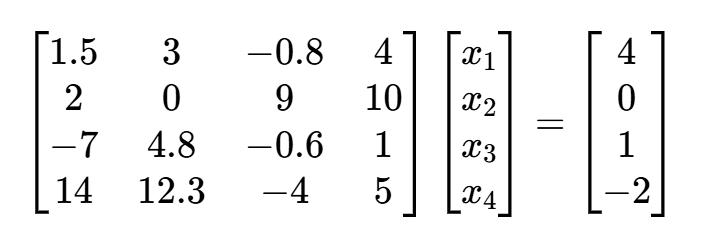
>> A = [1.5,3,-0.8,4;2,0,9,10;-7,4.8,-0.6,1;14,12.3,-4,5];
>> b = [4,0,1,-2]';
>> [L,U,y,x] = Doolittle(A,b)

4. 对称正定矩阵的三角分解(楚列斯基分解)法,平方根法
算法原理:“如果A为n阶对称正定矩阵,则存在一个实的非奇异下三角阵L,使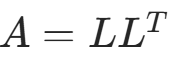 ,当限定L的对角元素为正时,这种分解是唯一的。”
,当限定L的对角元素为正时,这种分解是唯一的。”
“如果有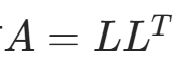 ,则求解Ax=b的问题就等价于求解两个三角形方程组:求解Ly=b,得y;求解
,则求解Ax=b的问题就等价于求解两个三角形方程组:求解Ly=b,得y;求解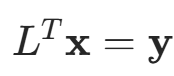 ,得x。”
,得x。”
算法步骤:
设A为n阶对称正定矩阵。
① 对于j=1,2,⋯,n,计算
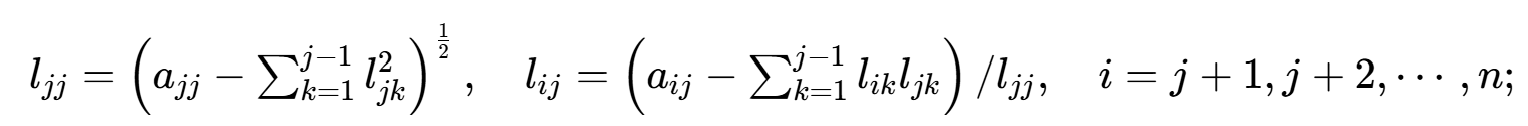
② 解Ly=b,求y:
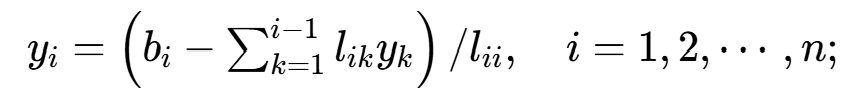
③ 解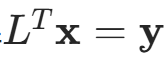 ,求x:
,求x:
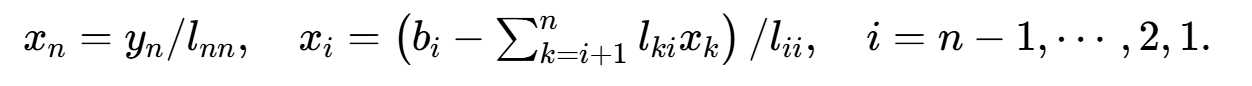
MATLAB 程序:
function [L,x] = cholesky_decomp(A,b)
% 楚列斯基分解法求解对称正定方程组 Ax = b
% 输入:A为对称正定矩阵,b为右端向量
% 输出:L为下三角矩阵,x为方程组的解
[m,n] = size(A); % 正确获取矩阵维度
% 输入检查
if m ~= n
disp('错误:系数矩阵必须为方阵');
return;
elseif m ~= length(b)
disp('错误:系数矩阵与右端向量维度不匹配');
return;
elseif norm(A - A') > 1e-10 % 允许微小浮点误差
disp('错误:系数矩阵必须为对称矩阵');
return;
end
% 初始化变量
x = zeros(n,1);
y = zeros(n,1);
L = zeros(n,n);
% 楚列斯基分解:计算下三角矩阵L
for k = 1:n
% 计算对角线元素L(k,k)
sum_diag = L(k,1:k-1) * L(k,1:k-1)'; % 内积求和
if (A(k,k) - sum_diag) <= 0
disp('错误:矩阵非正定,无法进行楚列斯基分解');
return;
end
L(k,k) = sqrt(A(k,k) - sum_diag);
% 计算非对角线元素L(i,k) (i > k)
if k < n
sum_off = L(k+1:n,1:k-1) * L(k,1:k-1)'; % 内积求和
L(k+1:n,k) = (A(k+1:n,k) - sum_off) / L(k,k);
end
% 求解Ly = b(前代过程)
sum_y = L(k,1:k-1) * y(1:k-1);
y(k) = (b(k) - sum_y) / L(k,k);
end
% 求解L'x = y(回代过程)
x(n) = y(n) / L(n,n);
for k = n-1:-1:1
sum_x = L(k+1:n,k)' * x(k+1:n);
x(k) = (y(k) - sum_x) / L(k,k);
end
end
数值实验
例 5 用楚列斯基分解法解方程组
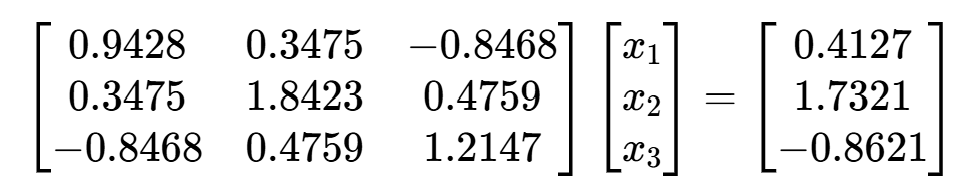
>> A = [0.9428, 0.3475, -0.8468; 0.3475, 1.8423, 0.4759; -0.8468, 0.4759, 1.2147];
>> b = [0.4127,1.7321,-0.8621]';
>> [L,x] = cholesky_decomp(A,b)

5. 改进平方根法
算法原理:“用平方根法求解对称正定方程组时,计算L的元素![]() 需要用到开方运算,为了避免开方,可采用分解式
需要用到开方运算,为了避免开方,可采用分解式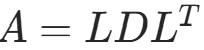 ,其中L为单位下三角阵,D为对角阵。”
,其中L为单位下三角阵,D为对角阵。”
“如果有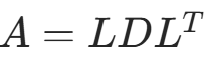 ,则求解Ax=b的问题就等价于求解两个三角形方程组:求解Ly=b,得y;求解
,则求解Ax=b的问题就等价于求解两个三角形方程组:求解Ly=b,得y;求解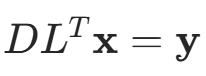 ,得x。计算L和D以及求解三角形方程组时不需要开方运算。”
,得x。计算L和D以及求解三角形方程组时不需要开方运算。”
算法步骤:
设A为n阶对称正定矩阵。为避免重复计算,引进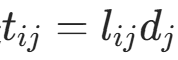 ,
,
① 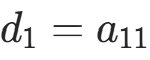 ,对于i=2,3,⋯,n,
,对于i=2,3,⋯,n,
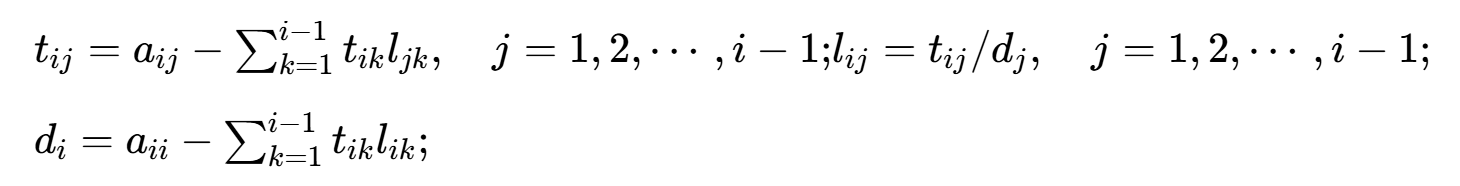
② 解Ly=b,求y:
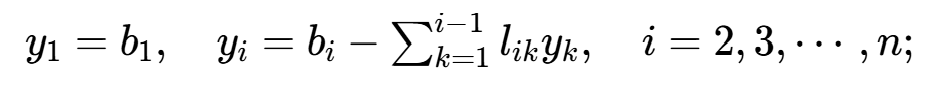
③ 解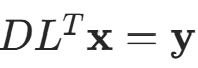 ,求x:
,求x:
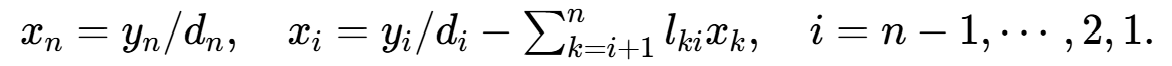
MATLAB 程序:
function [L,D,x] = LDL(A,b)
% A为对称正定的系数矩阵,b为右端向量,x为方程组的解
% L为单位下三角阵,D为对角矩阵
[m,n] = size(A);
if m ~= n
disp('系数矩阵非方阵'); return;
elseif m ~= length(b)
disp('系数矩阵和右端不匹配'); return;
end
if A - A' ~= 0
disp('系数矩阵非对称'); return;
end
L = eye(n); T = zeros(n);
d = zeros(n,1); x = zeros(n,1); y = zeros(n,1);
for k = 1:n
d(k) = A(k,k) - T(k,1:k-1) * L(k,1:k-1)';
if d(k) <= 0
disp('error'); return;
else
T(k+1:n,k) = A(k+1:n,k) - T(k+1:n,1:k-1) * L(k,1:k-1)';
L(k+1:n,k) = T(k+1:n,k)/d(k);
end
end
for i = 1:n
y(i) = b(i) - L(i,1:i-1) * y(1:i-1);
end
z = y./d;
for i = n:-1:1
x(i) = z(i) - L(i+1:n,i)' * x(i+1:n);
end
D = diag(d);
数值实验
例 6 用改进平方根法解方程组
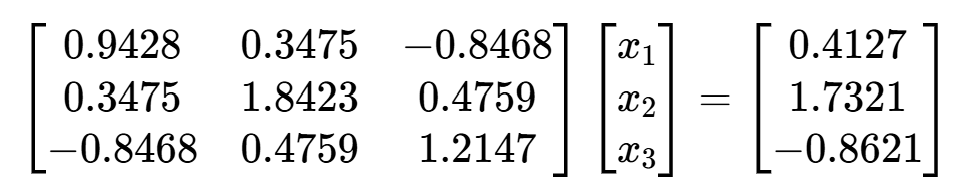
>> A = [0.9428, 0.3475, -0.8468; 0.3475, 1.8423, 0.4759; -0.8468, 0.4759, 1.2147];
>> b = [0.4127,1.7321,-0.8621]';
>> [L,D,x] = LDL(A,b)

6. 追赶法
算法原理:“当系数矩阵A为对角占优的三对角阵时,A满足直接三角分解的条件且可分解为两个三角矩阵的乘积A=LU,其中L和U分别为带宽为 2 的下、上三角阵。”
“如果有A=LU,则求解Ax=f的问题就等价于求解两个三角形方程组:求解Ly=f,得y;求解Ux=y,得x。”
算法步骤:
记三对角线线性方程组为Ax=f,即
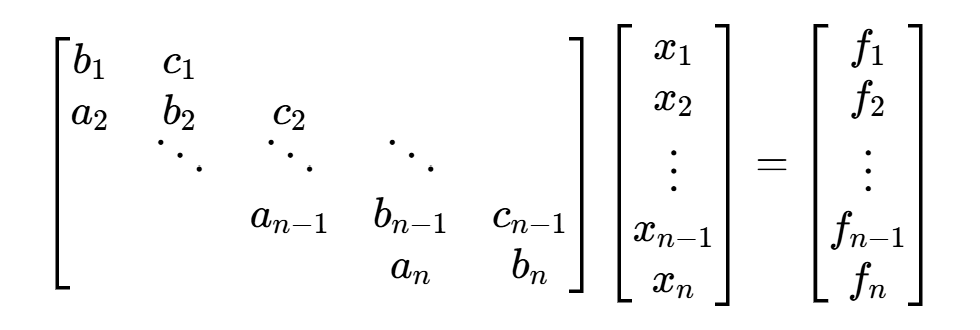
其中A=LR,其中

计算三角分解:
① 对于i=1,2,⋯,n−1,![]() ;
;
②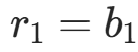 ,对于i=2,3,⋯,n,计算
,对于i=2,3,⋯,n,计算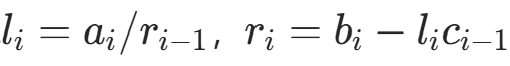 ;
;
求解Ly=f:
③ 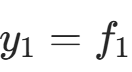 ,对于i=2,3,⋯,n,计算
,对于i=2,3,⋯,n,计算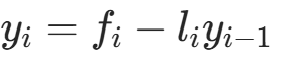 (追);
(追);
求解Rx=y:
④ 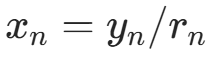 ,对于i=n−1,n−2,⋯,1,计算
,对于i=n−1,n−2,⋯,1,计算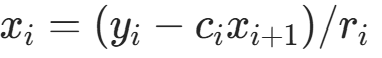 (赶)。
(赶)。
MATLAB 程序:
function x = zgf_(a,b,c,f)
% 为a系数矩阵-1对角线元素,b为对角线元素
% c为系数矩阵+1对角线元素,f为右端向量,x为方程组的解
a = [0 a]; % a的首个元素补零
n = length(b);
if n ~= length(f)
disp('向量长度不匹配'); return;
end
L(1) = b(1); u(1) = c(1)/L(1); % 追
for i = 2:n-1
L(i) = b(i) - a(i) * u(i-1); u(i) = c(i)/L(i);
end
L(n) = b(n) - a(n) * u(n-1); y(1) = f(1) /L(1);
for i = 2:n
y(i) = (f(i) - y(i-1) * a(i))/L(i);
end
x(n) = y(n); % 赶
for i = n-1:-1:1
x(i) = y(i) - u(i) * x(i+1);
end
数值实验
例 7 用追赶法解方程组
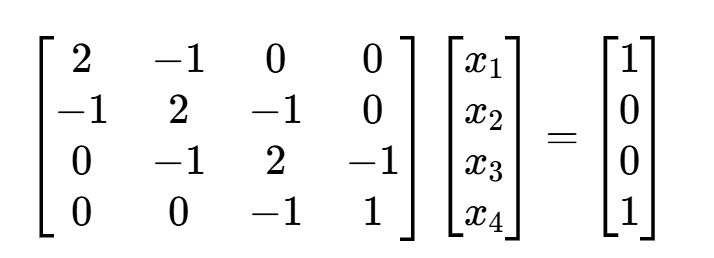
>> a = [-1, -1, -1];
>> b = [2,2,2,1];
>> c = [-1, -1, -1];
>> f = [1,0,0,1];
>> x = zgf_(a,b,c,f)

总结
本文介绍了求解线性方程组的几种数值方法及其MATLAB实现。主要内容包括:
1.高斯消去法及其MATLAB程序,通过消元转化为上三角矩阵后回代求解;
2.高斯列主元消去法,通过选主元减小误差,适用于病态方程组;
3.矩阵直接三角分解法(Doolittle分解),将矩阵分解为单位下三角和上三角矩阵;
4.对称正定矩阵的楚列斯基分解法(平方根法),利用对称正定性简化计算;
5.改进平方根法(LDL分解),避免开方运算;
6.追赶法,专门求解三对角线性方程组。
每种方法均给出算法原理、MATLAB实现代码和数值算例,重点分析了病态方程组的误差特性。这些方法在计算效率、数值稳定性等方面各有特点,适用于不同类型的线性方程组求解问题。
























 1423
1423

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








