【路径规划】蚁群算法的优化计算——旅行商问题(TSP)优化

摘要

旅行商问题（TSP）是一种经典的组合优化问题，其目标是找到一条遍历所有城市且总路程最短的环路。由于其计算复杂度高，求解大规模TSP问题往往依赖于启发式算法。本文研究了基于蚁群算法（Ant Colony Optimization, ACO）的TSP优化问题，通过实验验证了蚁群算法在求解TSP问题中的有效性。结果表明，经过若干次迭代后，蚁群算法能够找到一个较优的解决方案。

理论

蚁群算法模拟了自然界中蚂蚁通过信息素寻找最短路径的行为。蚂蚁在行进过程中会在路径上留下信息素，其他蚂蚁在选择路径时会优先选择信息素浓度较高的路径，进而逐渐收敛到最优路径。

在TSP问题中，蚁群算法的基本思想如下：

• 状态转移规则：蚂蚁根据当前城市与目标城市之间的距离和信息素浓度来选择下一步的城市。通常采用启发式函数来引导蚂蚁的搜索方向，选择概率为：

  

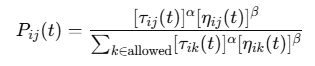
  其中， 𝜏𝑖𝑗(𝑡)是城市，𝑖 到城市 𝑗 之间的信息素浓度，𝜂𝑖𝑗(𝑡)是启发式函数（一般为距离的倒数），𝛼和𝛽分别为信息素权重和启发式权重。

• 信息素更新规则：蚂蚁完成一轮搜索后，根据路径长度来更新信息素浓度：

  

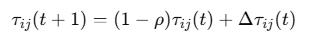
  其中，𝜌是信息素挥发系数，Δ𝜏𝑖𝑗(𝑡)是信息素增量，与路径的优劣相关。

通过多次迭代，蚁群算法逐步收敛到全局最优解。

实验结果

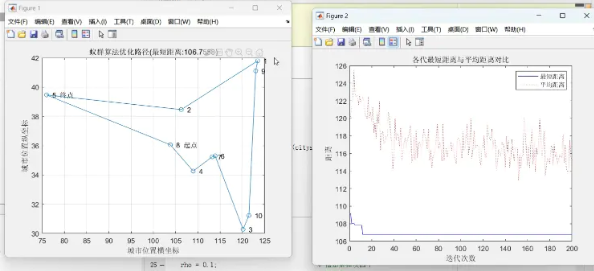
• 图1展示了蚁群算法求解TSP问题的最优解路径。从图中可以看出，经过10次迭代后，算法找到了一个较优的环路。

• 图2展示了随着迭代次数的增加，最优路径的变化情况。初期算法的路径长度波动较大，随着迭代次数的增加，路径长度逐渐收敛到较优值。

部分代码

% 参数设置
num_cities = 10;  % 城市数量
num_ants = 20;    % 蚂蚁数量
alpha = 1;        % 信息素重要性因子
beta = 5;         % 启发式因子重要性
rho = 0.5;        % 信息素挥发系数
num_iter = 200;   % 最大迭代次数

% 随机生成城市坐标
city_coords = rand(num_cities, 2) * 100;

% 初始化距离矩阵
dist_matrix = zeros(num_cities);
for i = 1:num_cities
    for j = i+1:num_cities
        dist_matrix(i,j) = sqrt(sum((city_coords(i,:) - city_coords(j,:)).^2));
        dist_matrix(j,i) = dist_matrix(i,j);
    end
end

% 初始化信息素矩阵
pheromone = ones(num_cities) * 0.1;

% 蚁群算法主循环
for iter = 1:num_iter
    % 初始化每只蚂蚁的路径
    paths = zeros(num_ants, num_cities);
    path_lengths = zeros(num_ants, 1);
    
    for ant = 1:num_ants
        % 随机选择起点城市
        current_city = randi(num_cities);
        visited = false(1, num_cities);
        visited(current_city) = true;
        path = zeros(1, num_cities);
        path(1) = current_city;
        
        % 构建路径
        for step = 2:num_cities
            % 计算选择下一个城市的概率
            prob = (pheromone(current_city, :) .^ alpha) .* ((1 ./ dist_matrix(current_city, :)) .^ beta);
            prob(visited) = 0;  % 已访问的城市概率为0
            prob = prob / sum(prob);  % 归一化
            
            % 根据概率选择下一个城市
            next_city = find(rand <= cumsum(prob), 1);
            path(step) = next_city;
            visited(next_city) = true;
            current_city = next_city;
        end
        
        % 记录路径及其长度
        paths(ant, :) = path;
        path_lengths(ant) = sum(dist_matrix(sub2ind(size(dist_matrix), path(1:end-1), path(2:end))));
    end
    
    % 更新信息素
    pheromone = (1 - rho) * pheromone;  % 信息素挥发
    for ant = 1:num_ants
        for step = 1:num_cities-1
            pheromone(paths(ant, step), paths(ant, step+1)) = pheromone(paths(ant, step), paths(ant, step+1)) + 1 / path_lengths(ant);
        end
    end
end

% 绘制最优路径
[min_length, best_ant] = min(path_lengths);
best_path = paths(best_ant, :);
figure;
plot(city_coords(best_path, 1), city_coords(best_path, 2), 'o-');
title(sprintf('最优路径长度: %.2f', min_length));
xlabel('X 坐标');
ylabel('Y 坐标');

% 绘制收敛曲线
figure;
plot(1:num_iter, path_lengths);
xlabel('迭代次数');
ylabel('路径长度');
title('最优路径长度变化');

参考文献

❝

1. Dorigo, M., & Gambardella, L. M., "Ant Colony System: A Cooperative Learning Approach to the Traveling Salesman Problem," IEEE Transactions on Evolutionary Computation, vol. 1, no. 1, pp. 53-66, 1997.

2. Bonabeau, E., Dorigo, M., & Theraulaz, G., "Swarm Intelligence: From Natural to Artificial Systems," Oxford University Press, 1999.

3. Kennedy, J., & Eberhart, R. C., "Particle Swarm Optimization," Proceedings of IEEE International Conference on Neural Networks, pp. 1942-1948, 1995.

（文章内容仅供参考，具体效果以图片为准）