C C++最新十道题带你手撕二叉树(1)，2024年最新最新BAT大厂面试者整理的C C++面试题目模板

最新推荐文章于 2024-11-06 19:55:44 发布

2401_84973716

最新推荐文章于 2024-11-06 19:55:44 发布

阅读量537

点赞数 11

分类专栏：程序员文章标签： c语言 c++ 学习

本文链接：https://blog.csdn.net/2401_84973716/article/details/138887563

版权

程序员专栏收录该内容

43 篇文章 2 订阅

订阅专栏

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化的资料的朋友，可以添加戳这里获取

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

    return false;
}

//判断左右子树
return isUnivalTree(root->left)&&isUnivalTree(root->right);

}



> 
> 问：为什么只需要判断根节点和左右子节点是否一样就可以了？
> 
> 
> 答：注意这个-传递性，如果根节点和其左右子节点分别相同了，那么在递归的时候，之前的左右子节点就会变成根节点，此时就是在保持前面一样的前提下来判断新的根节点和新的根节点的左右子节点是否相同，优点类似链表，就是说链表的第一和第二个节点是相同的之后，然后判断第二和第三个节点是否是相同的，如果第二和第三个节点是相同的之后，那么第一和第三个节点也必然是相同的，依此类推，当这样的每个比较都成立之后，就说明整个二叉树就是等值二叉树。
> 
> 
> 


当然，还有一种不是很好的写法，这种写法虽然也能通过，和上面的思路来说本质上并没有太大的区别（甚至定义的那个全局变量还显得有些多余），并不推荐这种写法，**因为这种写法定义了一个全局变量，在OJ题中最好不要定义全局变量和静态变量，因为后台程序可能会多次调用这个程序，flag中可能还存储着上一次的结果，在下一次调用时容易出问题**。代码如下：

bool flag = true;//默认最开始就是单值二叉树
bool isUnivalTree(struct TreeNode* root){
if(root==NULL)
{
flag = true;
return flag;
}

if(root->left && root->val!=root->left->val)
{
    flag = false;
    return flag;
}
if(root ->right &&root->val!=root->right->val )
{
    flag = false;
    return flag;
}
return isUnivalTree(root->left)&&isUnivalTree(root->right);

}


## 2. 相同的树


题目：


![image-20220413164221936](https://img-blog.csdnimg.cn/img_convert/2690a58e54a33219c945c3f24083610a.png)


代码：

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
//都是空树
if(pNULL&&qNULL)
return true;

//有一个为空
if(p == NULL || q == NULL)
    return false;

//都不为空
if(p->val!=q->val)
    return false;

//递归比较左右子树
return isSameTree(p->left, q->left)&&isSameTree(p->right, q->right);

}


## 3. 对称二叉树


题目：


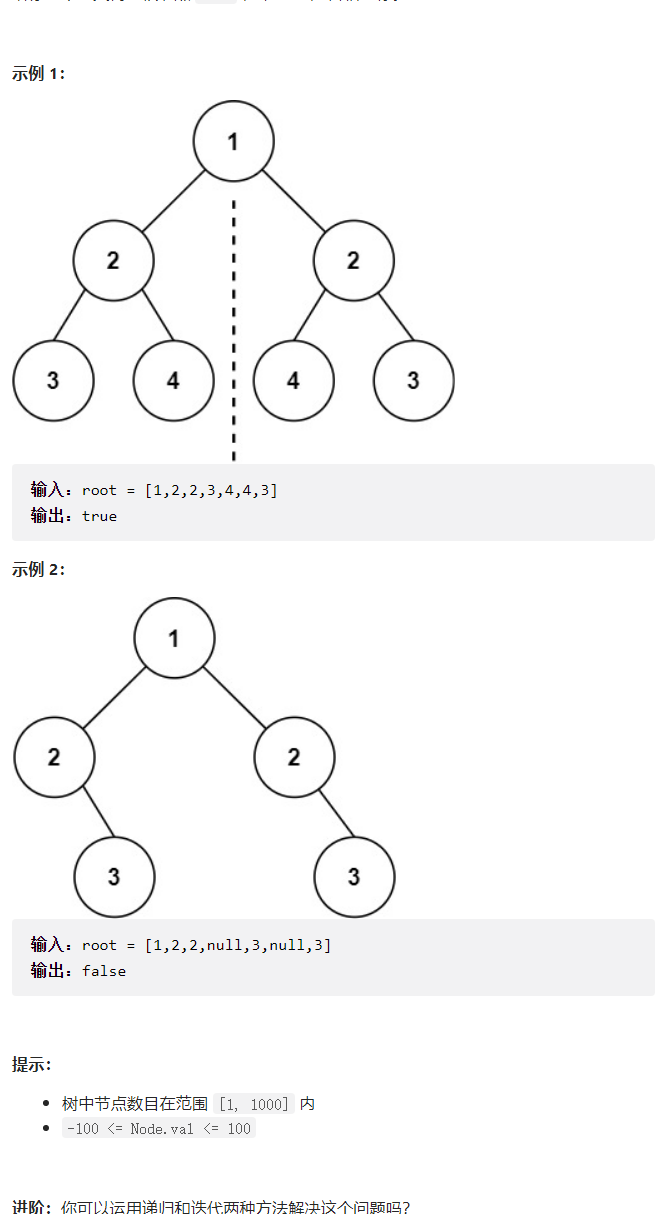
![image-20220413164452305](https://img-blog.csdnimg.cn/img_convert/99d999704c2034f2df8767de73fbf784.png)


代码：

bool isSymmetricTree(struct TreeNode* p,struct TreeNode* q)//辅助函数
{
//两个节点均为空的情况
if(pNULL && qNULL)
{
return true;
}

//两个节点有一个不为空的情况
if(p == NULL || q == NULL)
{
    return false;
}

//两个节点是否相等的情况并对两个节点进行递归判断，注意镜像相反
return p->val == q->val && isSymmetricTree(p->left,q->right)&&isSymmetricTree(p->right,q->left);

}

bool isSymmetric(struct TreeNode* root){
//根节点为空的情况
if(root == NULL)
{
return true;
}

//根节点不为空的情况
return isSymmetricTree(root->left,root->right);

}


## 4. 二叉树的前序遍历


题目：


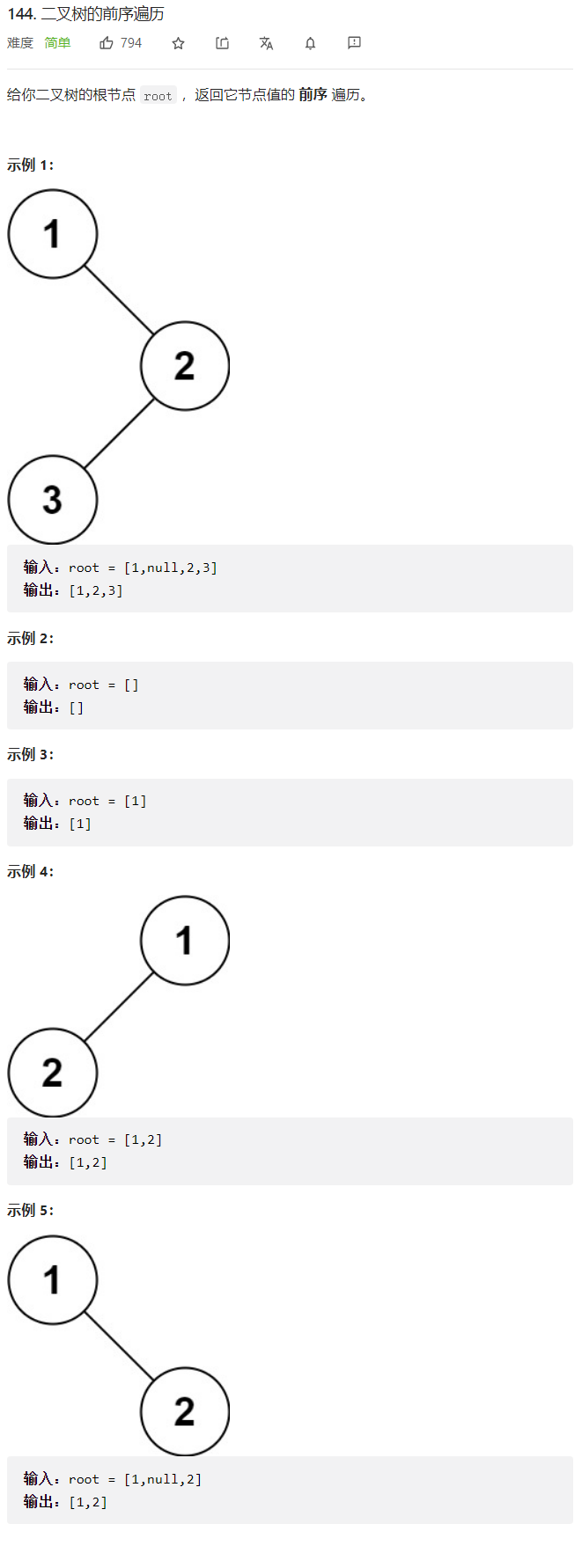
![image-20220413171225966](https://img-blog.csdnimg.cn/img_convert/907cfd71a4e1dfb62734ac11af7d35dd.png)


代码：

int BTreeSize(struct TreeNode* root)//计算二叉树元素的数目
{
return root == NULL ? 0 : 1 + BTreeSize(root->left) + BTreeSize(root->right);
}

void _preorder(struct TreeNode* root,int *a,int *i)//辅助函数
{
if(root == NULL)//空的时候直接返回
{
return;
}
//1.先遍历根节点
a[*i] = root->val;//将有值得存储到开辟得数组空间中
(*i)++;//数组下标进行自增操作
//2.遍历左子树
_preorder(root->left,a,i);//对左子树进行操作
//3.遍历右子树
_preorder(root->right,a,i);//对右子树进行操作
}

int* preorderTraversal(struct TreeNode* root, int* returnSize){
int count = BTreeSize(root);//计算题目所给二叉树元素得数目
int *a = malloc(sizeof(int)*count);//开辟数组存储二叉树元素
assert(a);//防止malloc开辟失败
*returnSize = count;//存储数组元素得数目
int i = 0;//当作数组下标来存储二叉树元素
_preorder(root,a,&i);
return a;
}


## 5. 二叉树的中序遍历


题目：


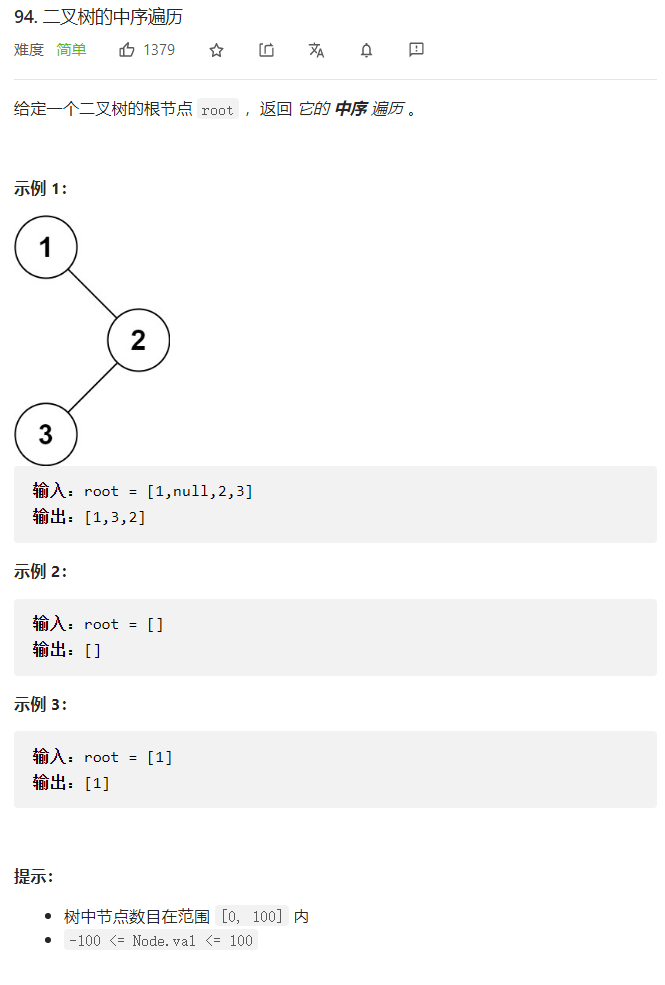
![image-20220413200702041](https://img-blog.csdnimg.cn/img_convert/3119af2f12d0bbdfe0475cc2331525a9.png)


代码：

int BTreeSize(struct TreeNode* root)//计算二叉树元素的数目
{
return root == NULL ? 0 : 1 + BTreeSize(root->left) + BTreeSize(root->right);
}

void _inorder(struct TreeNode* root,int *a,int *i)//辅助函数
{
if(root == NULL)//空的时候直接返回
{
return;
}
//1. 遍历左子树
_inorder(root->left,a,i);//对左子树进行操作
//2.遍历根节点
a[*i] = root->val;//将有值得存储到开辟得数组空间中
(*i)++;//数组下标进行自增操作
//3.遍历右子树
_inorder(root->right,a,i);//对右子树进行操作

}

int* inorderTraversal(struct TreeNode* root, int* returnSize){
int count = BTreeSize(root);//计算题目所给二叉树元素得数目
int *a = malloc(sizeof(int)*count);//开辟数组存储二叉树元素
assert(a);//防止malloc开辟失败
*returnSize = count;//存储数组元素得数目
int i = 0;//当作数组下标来存储二叉树元素
_inorder(root,a,&i);
return a;
}


## 6. 二叉树的后序遍历


题目：


![image-20220413201330198](https://img-blog.csdnimg.cn/img_convert/ac8b4a1a14a1307c149f09ebefe9f112.png)


代码：

int BTreeSize(struct TreeNode* root)//计算二叉树元素的数目
{
return root == NULL ? 0 : 1 + BTreeSize(root->left) + BTreeSize(root->right);
}

void _postorder(struct TreeNode* root,int *a,int *i)//辅助函数
{
if(root == NULL)//空的时候直接返回
{
return;
}
//1. 遍历左子树
_postorder(root->left,a,i);//对左子树进行操作
//2.遍历右子树
_postorder(root->right,a,i);//对右子树进行操作
//3.遍历根节点
a[*i] = root->val;//将有值得存储到开辟得数组空间中
(*i)++;//数组下标进行自增操作
}

int* postorderTraversal(struct TreeNode* root, int* returnSize){
int count = BTreeSize(root);//计算题目所给二叉树元素得数目
int *a = malloc(sizeof(int)*count);//开辟数组存储二叉树元素
assert(a);//防止malloc开辟失败
*returnSize = count;//存储数组元素得数目
int i = 0;//当作数组下标来存储二叉树元素
_postorder(root,a,&i);
return a;
}


## 7. 另一棵树的子树


题目：


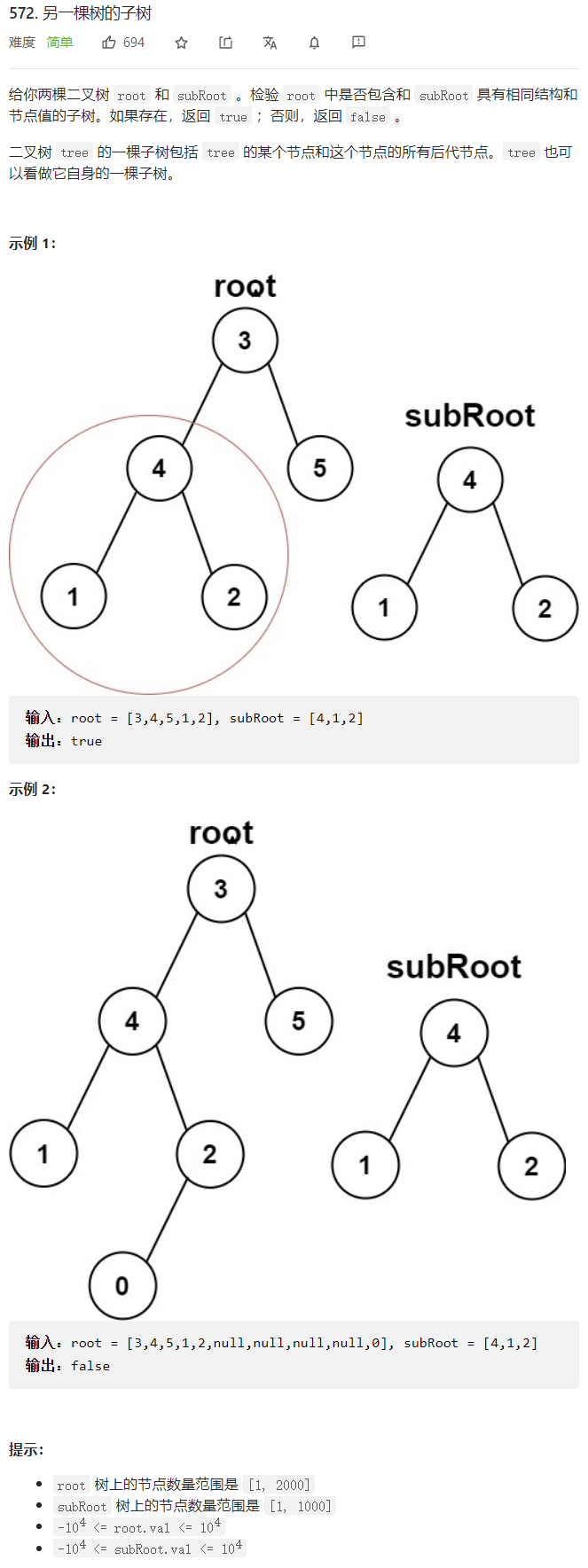
![image-20220413201922146](https://img-blog.csdnimg.cn/img_convert/3c7be8328ecdfc5f0739bfe42f102db1.png)


代码：

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
//都是空树
if(pNULL&&qNULL)
return true;

//有一个为空
if(p == NULL || q == NULL)
    return false;

//都不为空
if(p->val!=q->val)
    return false;

//递归比较左右子树
return isSameTree(p->left, q->left)&&isSameTree(p->right, q->right);

}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
if(root == NULL)
return false;
return isSameTree(root,subRoot) || isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}


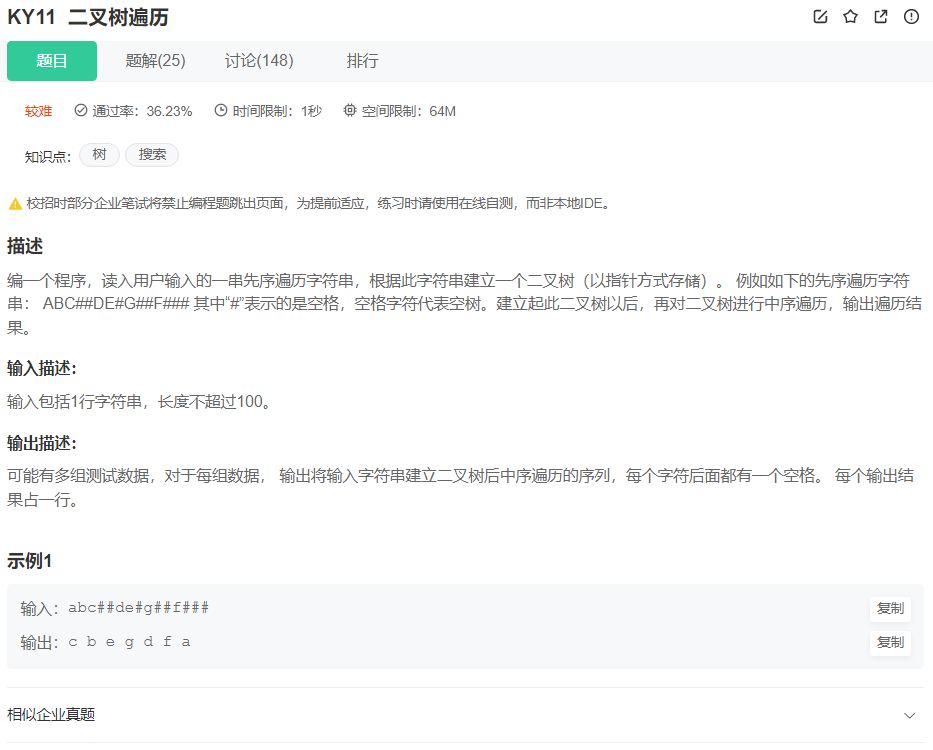
## 8. 二叉树的遍历


题目：


![image-20220415191551296](https://img-blog.csdnimg.cn/img_convert/4028a480ca5b7ca54b22bade9eb90beb.png)


![img](https://img-blog.csdnimg.cn/img_convert/8ba743f0405fbe9eab2cae8f72bd7ddd.png)
![img](https://i-blog.csdnimg.cn/blog_migrate/cf05b64faba9bce1bfdf9e35a876e328.png)

**网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。**

**[需要这份系统化的资料的朋友，可以添加戳这里获取](https://bbs.csdn.net/topics/618668825)**


**一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**

g)


[外链图片转存中...(img-Jh30lTly-1715728629217)]
[外链图片转存中...(img-8jJdevNB-1715728629218)]

**网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。**

**[需要这份系统化的资料的朋友，可以添加戳这里获取](https://bbs.csdn.net/topics/618668825)**


**一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**