AI线性算法的“视觉”理解-线性代数（2）

前言-PREFACE

通过上一篇文章，我们已经初步掌握了线性代数作为是人工智能世界通用“语言”的基本概念和“语法”。线性代数作为人工智能最重要的基础数学学科之一，应用非常广泛，在某些情况下，可能会涉及较为复杂和抽象运算，为了更加直观理解运算过程，深入洞察和分析运算本质，从几何和空间等“视觉”角度的探讨线性代数的运算过程非常有意义。

线性代数的核心在于对空间的变换和操作。既然从“视觉”角度来理解线性代数，那么线性代数的“视觉”表示和线性变换是主要的两个概念，但是在高维空间中，可视化变得非常困难，只能通过数学的方法来理解它们，本文主要以线性代数的二维和三维视觉来进行探讨，读者可以以此来理解和类推更高维情况。

线性代数的“视觉”理解-VISIBLE LINEAR ALGEBRA

 线性代数的视觉表示 

首先我们先来了解一下线性代数的概念的“视觉”表示，然后才能更好理解变化过程。

1、向量的表示

初学者经常会困惑于向量到底是被视为空间中的一个点，还是为带有方向和长度的线段。其实两种理解都对，虽然将向量视为空间中的点的情况更常见，但究竟如何选择主要取决于具体的应用场景和问题的背景，下面分别针对不同的情况进行举例说明：

• 向量作为空间中的点：

  • 表示数据点：在高维空间中，向量常用于表示数据集中的一个点。每个维度对应一个特征，向量的坐标表示该点在各个维度上的取值。当我们主要关注向量之间距离进行相似性计量时，向量作为空间的点进行点间距离计算会更适用。

  • 应用场景：在回归、分类、聚类等任务中，我们通常将样本数据看作是高维空间中的点，利用这些点的位置和相对距离来进行分析和建模，下面是二维空间的相关示意图：

    

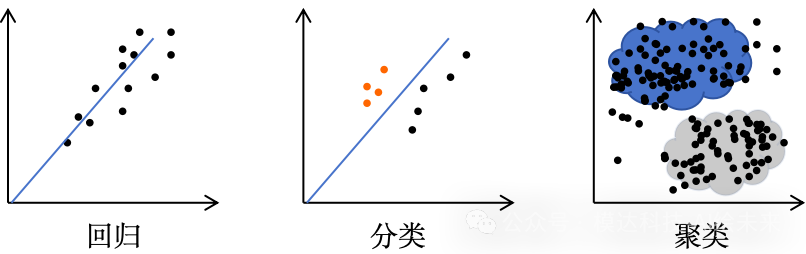
• 向量作为带方向和长度的线段：

  • 表示变化或差异：在某些情况下，向量被理解为具有方向和长度的线段，可以更直观地理解向量间运算，以及图像的旋转、缩放、平移等几何变换。

  • 应用场景：以下为向量加法（减法可以以反方向类推）、乘法的示意图，其中：向量a、b相加结果为以a、b为有向线段组成的平行四边形的对角线c，也可以理解为从原点出发先沿向量a方向走a模长的距离，然后再沿向量b方向走b模长的距离，然后到达向量c，该结论可以以几何的方式进行推导，相对比较简单，本文不再赘述；向量a乘以标量r等于在a相同方向进行缩放，如果r为负值，则为反方向缩放；向量a、b间点积为a在b上投影（a的模长乘以夹角余弦值，即|a|•cosθ）的长度乘以b的模长，结果是一个标量，用于表示a，b间的相似程度。

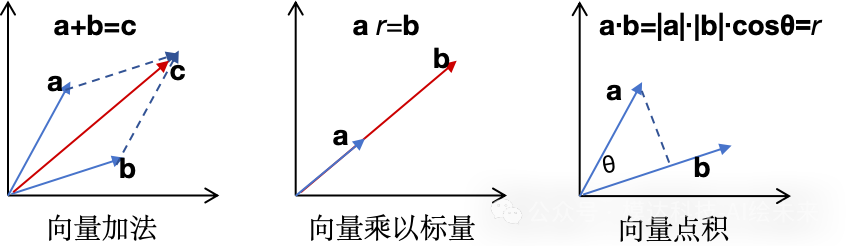
在优化算法（如梯度下降）中，向量通常表示梯度或步长，它们指出了函数值变化的方向和大小。神经网络的权重更新也可以看作是向量的方向和长度的变化。

2、向量空间的表示

满足加法封闭性和标量乘法封闭性的向量集合组成了向量空间，这个向量空间的相关运算满足交换律、结合律、分配律等，以及存在零向量和负向量等性质。每个向量空间都有一个基，基是一组线性无关的向量，它们可以生成整个向量空间。向量空间的维度是其基中向量的数量。

对于二维实数R向量空间可以想象成为在二维空间所有点（x，y）的集合，组成一个无限延伸的二维平面，同样的，对于三维实数R向量空间可以想象成为在三维空间所有点（x，y，z）的集合，组成一个无限延伸的三维平面，而如果向量元素为整数，则为向量空间为离散型。

子空间是向量空间的一个子集，它本身也是一个向量空间。即子空间继承了向量空间的加法和数乘运算。例如：在二维平面上，所有经过原点的直线构成一个子空间；在三维空间中，所有经过原点的平面也构成一个子空间，可以用下图形象表示：

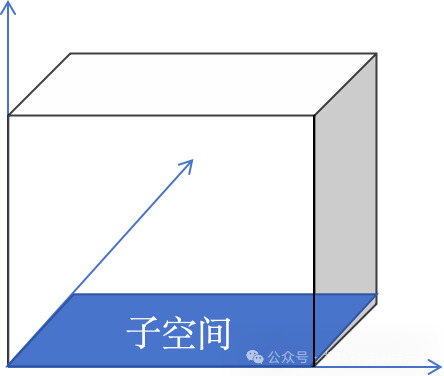
 线性代数的变换 

1、向量的空间变换

矩阵与向量的乘法相当于对向量进行空间的变换，可以将矩阵视为一种函数，函数的效果包括降维、升维或是原空间内的变换。该变换在在人工智能领域有着广泛而深入的应用，包括特征提取、主成因分析、神经网络参数优化等各个方面。以下公式以矩阵A作为函数，与向量x相乘后的计算结果为向量b，不同情况下分别表示了向量x的变化：

1）降维（三维变成二维）（降维通常用于数据压缩、特征提取或可视化）：

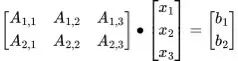
2）空间内变换（维度无变化）：

3）升维（二维变成三维）（升维可以帮助改善模型的效果）：

2、向量空间与线性方程组

假如有以下线性方程组

可以表示为A

x=b，其中A是矩阵：

x、b是向量：

我们将矩阵A的列向量视为从原点出发的不同方向，其列向量生成了一个子空间，称为矩阵A的列空间，列空间中的每一个点都可以通过矩阵 A的列向量的线性组合到达。线性方程的求解过程就是确认向量b是否可以由矩阵列向量的线性组合生成，以及有多少种方式生成，而向量x的每个元素为矩阵A 对应列向量的线性变化的系数。线性方程的解可以分为以下几种情况：

有解且唯一：如果矩阵A的列向量线性无关且矩阵满秩（即秩等于列数），那么线性方程组有唯一解。这意味着从原点到向量b只有一条路径。所有列向量的线性组合只能有一个唯一的方式生成b。

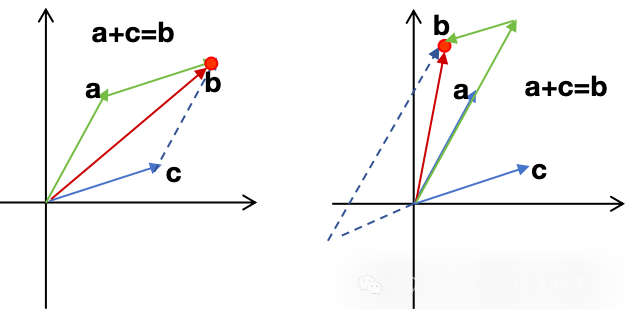
例如：在二维空间，两个线性无关的向量a、c通过向量x对应分量的线性变化，到达向量b的过程的两种情况，其他情况读者可自行分析。

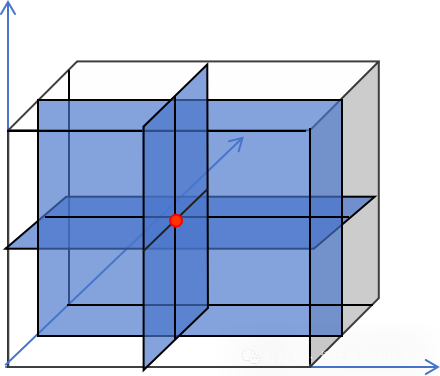
在三维空间，三个方向上切面上的直线交互点只有一个，这个交互点（下图红色点）就是结果向量b。

• 有解且有无穷多解：如果矩阵A的列向量线性相关，列空间的维度小于列数，方程组将可能有无穷多解。这意味着存在无数条路径可以从原点到达b。这些路径形成了一个线性子空间，这个子空间中的每一点都可以通过不同的线性组合方式生成b。

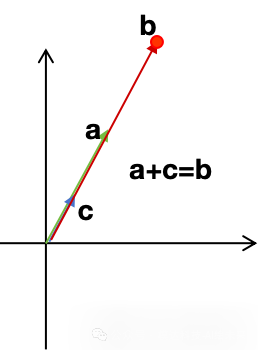
  例如：在二维平面，两个线性相关的向量a、c在同一条直线上，如果目标向量b与向量a、c共线，则也存在无穷多个解。

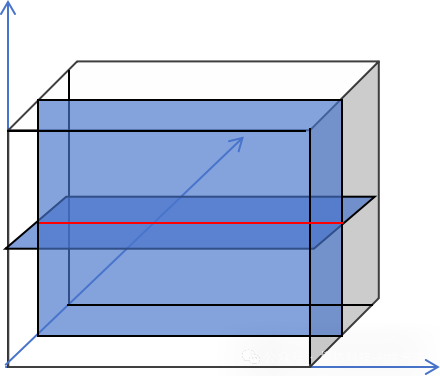
• 在三维空间，如果某两个列向量线性相关，则这两个列向量只能线性变换在同一平面，立体三个切面少了一个平面，剩下两个平面的交集为一条直线（下图红色线），如果向量b在这条相交的直线上，这样解就变成了无穷。

  

• 无解：如果b不在矩阵A的列空间中，方程组无解。这意味着没有任何路径可以通过矩阵A的列向量从原点出发到达b。b 位于列空间之外，无法通过任何线性组合生成。

  例如：在二维平面，如果向量c不在向量a、b共线的直线上，则无论怎样线性变换，也无法到达c点。

  

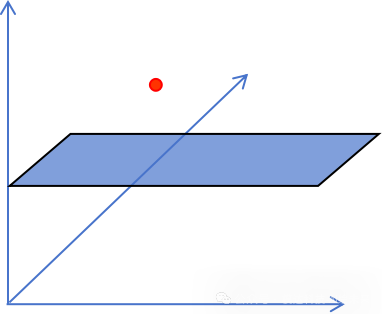
  在三维空间，下图如果矩阵A的列向量空间为一个平面，无论如何进行线性变换也到达不了三维空间红色的点。

  

结语-EPILOGUE

通过上述内容，将向量和矩阵运算过程和结果可视化，使得抽象的计算更加形象和可理解，帮助大家更快掌握线性代数中计算原理。当然上述例子只是描述了容易展示的二维和三维空间的情况，更高维空间的情况读者可以此为例进行类推。