数学建模小白——线性规划

我们高中阶段其实就学过线性规划的知识，但是那个时候可能感觉不太重要，带你们重新回忆一下。

这是高中时期解决此类题型的一般步骤：

定义决策变量：确定问题中需要做出决策的变量。

建立目标函数：根据问题要求，确定要最大化或最小化的函数。

列出约束条件：根据问题的实际要求，列出所有可能的约束条件，这些约束条件通常以线性不等式或等式的形式出现。

绘制可行域：在坐标系中绘制出所有约束条件所定义的可行域。

寻找最优解：在可行域的顶点处计算目标函数的值，以确定最优解。

检验解的可行性：确保找到的最优解满足所有的约束条件。

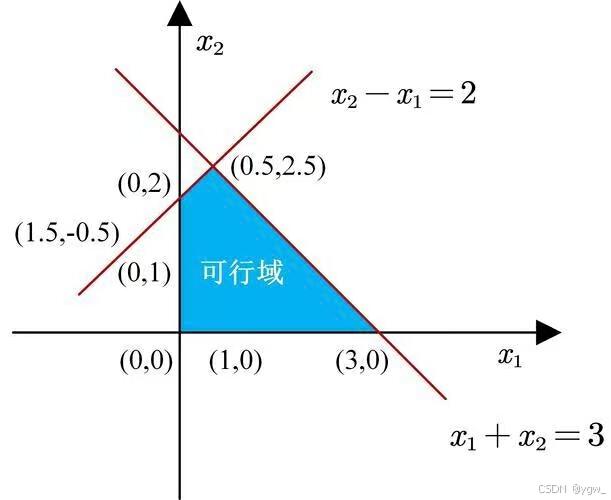
看到这个图大家是不是想起来了，其实到数学建模这里线性规划也没有那么神秘，只不过它不再局限于纸上了，你要用你所学过的编程语言表示出来解出来。

而大家期待的线性规划最重要的三点：决策变量、目标函数、约束条件

对于线性规划的标准形式：

目标函数：

约束条件:

                 

                  

                  

                 

这里就不细讲了，最后告诉大家如果大一新生想入手数学建模，从线性规划开始比较容易。