概率密度图详解

概率密度图是一种用于描述连续型随机变量概率分布的图形。
 
从形状上看，它可以呈现出多种不同的形式，可能是钟形曲线（如正态分布的概率密度图）、偏态曲线等。
 
从功能上，它通过图形直观地展示了随机变量在不同取值区间上的相对可能性大小。曲线下的面积代表了随机变量在相应区间内取值的概率。
 
概率密度图通常以横坐标表示随机变量的取值，纵坐标表示概率密度。它不属于传统意义上的几何图形分类，而是一种在统计学和概率论领域中用于分析和可视化概率分布的特定图形。

1. 概率密度图的解读方法包括：密度图的峰值位置反映数据的集中趋势，比如均值或中位数。
2. 密度图的宽度表明数据的离散程度，曲线越宽，数据的变异性越大。
3. 密度图的尾部可能出现小的峰，表明数据中存在异常值或次要的群体。
4. 可以通过在同一坐标轴上绘制多个不同组的密度图来比较它们的分布差异。
5. 密度图的y轴表示概率密度，可以了解数据在某个区间内出现的概率。

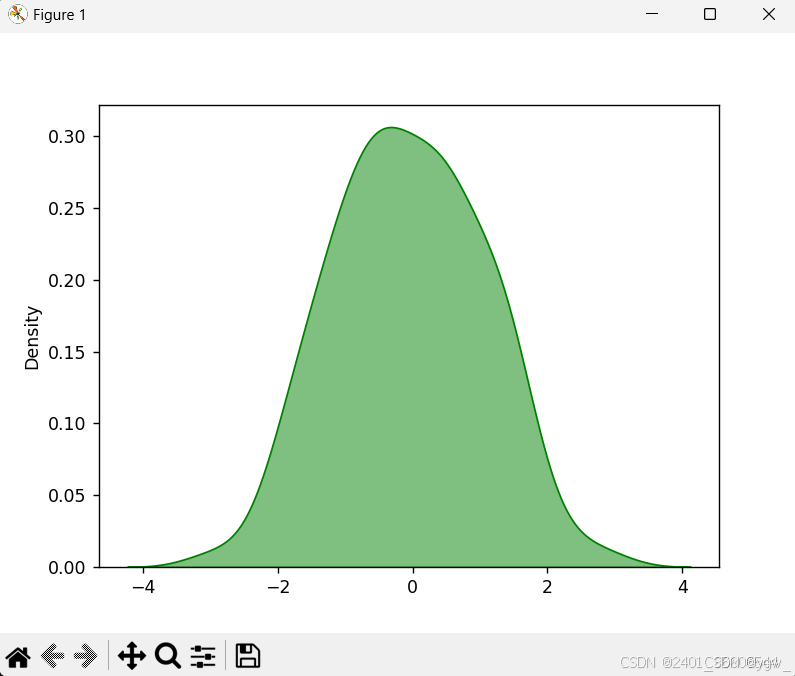
概率密度图（Probability Density Function, PDF）是统计学中用来描述连续型随机变量取值概率分布的一种图形表示方法。以下是如何阅读和理解概率密度图的一些基本步骤：

1. 理解横轴和纵轴：

- 横轴（X轴）代表随机变量的可能取值范围。

- 纵轴（Y轴）代表概率密度，即随机变量取特定值的概率。注意，纵轴的值不是概率本身，而是概率密度。

2. 曲线形状：

- 曲线下的面积表示随机变量取值的总概率，理论上应该等于1。

- 曲线的形状可以是对称的，也可以是不对称的（偏斜分布）。

3. 曲线下的面积：

- 曲线下的任何一段面积表示随机变量落在该区间内的概率。

- 例如，如果曲线下的某段面积是0.3，那么随机变量落在这个区间的概率是30%。

4. 曲线的峰值：

- 曲线的最高点通常表示随机变量最可能取值的区间，即众数。

5. 曲线的尾部：

- 对于正态分布，曲线的尾部表示极端值出现的概率。尾部越长，极端值出现的概率越高。

- 对于其他分布，如指数分布或均匀分布，曲线的尾部可能有不同的含义。

6. 曲线的对称性：

- 如果曲线关于某一点对称，那么这个分布是对称的。对称分布的均值、中位数和众数相等。

- 如果曲线不对称，那么这个分布是偏斜的。偏斜分布的均值、中位数和众数可能不同。

7. 多峰分布：

- 有些概率密度图可能有多个峰值，这表示随机变量的取值可能集中在几个不同的区间内。

8. 标准差和方差：

- 曲线的宽度可以反映随机变量的离散程度。曲线越宽，随机变量的取值越分散，方差越大；曲线越窄，随机变量的取值越集中，方差越小。

通过这些基本的步骤，你可以更好地理解和分析概率密度图所提供的信息。记住，概率密度图只是随机变量分布的一种表示方式，实际应用中还需要结合其他统计量和分析方法。