what is 堆

良木林

已于 2025-04-28 19:24:23 修改

阅读量723

点赞数 29

文章标签： c语言数据结构算法排序算法

于 2025-04-27 17:40:18 首次发布

本文链接：https://blog.csdn.net/2401_87805056/article/details/147565269

版权

堆

@jarringslee

堆作为一种重要的数据结构，在实际开发中有着广泛的应用，如排序算法、优先队列等。

你还记得二叉树嘛

堆本质上是一种特殊的二叉树。

（一）二叉树的定义

二叉树是一种树数据结构，它最多有两个子节点，分别称为左子节点和右子节点。二叉树可以是空树，也可以由一个根节点和两棵互不相交的左子树和右子树组成。

（二）二叉树的性质

1. 第 i 层最多有 2^{i-1} 个节点（i≥1）。
2. 深度为 h 的二叉树最多有 2^h -1 个节点（h≥1）。
3. 对于任何一棵非空二叉树，如果叶子节点数为 n0，度为 2 的节点数为 n2，则 n0 =n2 +1。

（三）完全二叉树

完全二叉树是除最后一层外，每一层的节点数都达到最大值，且最后一层的节点都靠左对齐。完全二叉树具有以下性质：

完全二叉树的第 i 层节点的父节点为(i-1)/2
完全二叉树的第 i 层节点的左孩子节点为 2i +1。
完全二叉树的第 i 层节点的右孩子节点为 2i +2。

例如：

这个结构就满足完全二叉树，而下面这个不是：

（因为第二层的右子树空缺后左边又出现了子节点）

什么是堆。

（一）堆的定义

堆是一种特殊的完全二叉树，它满足堆的性质：每个父节点的值都大于或等于（大顶堆）或小于或等于（小顶堆）其子节点的值。大顶堆中父节点的值总是大于或等于子节点的值，而小顶堆则相反。

（二）堆的分类

大顶堆 ：父节点的值总是大于或等于子节点的值。
小顶堆 ：父节点的值总是小于或等于子节点的值。

（三）堆的存储结构

堆通常使用数组来存储，因为完全二叉树的数组存储方式非常高效。在数组中，第 i 个元素的左孩子位于 2i +1 位置，右孩子位于 2i +2 位置，父节点位于 \lfloor (i-1)/2 \rfloor 位置。

（四）堆的示例

假设我们有一个数组 [45, 32, 28, 16, 11, 19, 13]，可以将其构造成一个大顶堆：

        45
      /    \
    32      28
   /  \    /  \
 16   11 19   13

在数组中的存储顺序是 [45, 32, 28, 16, 11, 19, 13]。

三、堆的实现

（一）堆的存储

typedef int DataType;
typedef struct Heap {
    DataType* a; //存放堆元素的数组
    int size;    //当前堆中元素的个数
    int capacity; //堆的最大容量
} Heap;

（二）堆的初始化

#include <stdlib.h>
#include <stdio.h>
#include <assert.h>

void HeapInit(Heap* php) {
    assert(php);
    php->a = (DataType*)malloc(sizeof(DataType) * 4);
    if (php->a == NULL) {
        perror("malloc fail");
        return;
    }
    php->size = 0;
    php->capacity = 4;
}

（三）堆的插入（向上调整）

当向堆中插入一个元素时，需要维护堆的性质。插入操作分为两步：首先将新元素添加到数组的末尾，然后通过向上调整来恢复堆的性质。

void AdjustUp(DataType* a, int child) {
    int parent = (child - 1) / 2;
    while (child > 0) {
        if (a[child] > a[parent]) {
            swap(&a[child], &a[parent]);
            child = parent;
            parent = (child - 1) / 2;
        } else {
            break;
        }
    }
}

void HeapPush(Heap* php, DataType x) {
    assert(php);
    if (php->size == php->capacity) {
        DataType* tmp = (DataType*)realloc(php->a, sizeof(DataType) * php->capacity * 2);
        if (tmp == NULL) {
            perror("realloc fail");
            return;
        }
        php->a = tmp;
        php->capacity *= 2;
    }
    php->a[php->size] = x;
    php->size++;
    AdjustUp(php->a, php->size - 1);
}

（四）堆的删除（向下调整）

删除堆顶元素后，需要将堆尾元素移到堆顶，然后通过向下调整来恢复堆的性质。

void AdjustDown(DataType* a, int n, int parent) {

    int child = 2 * parent + 1;
    

    while (child < n) {
 
        if (child + 1 < n && a[child] < a[child + 1]) {
            child++;
        }

        if (a[child] <= a[parent]) {
            break;
        }

        DataType temp = a[child];
        a[child] = a[parent];
        a[parent] = temp;
        
        parent = child;
        child = 2 * parent + 1;
    }
}

// 删除堆顶元素的函数
void HeapPop(Heap* php) {

    assert(php);
    
    assert(!empty(php));
    
    swap(&php->a[0], &php->a[php->size - 1]);
    php->size--；
    AdjustDown(php->a, php->size, 0);
}

// 获取堆顶元素的函数
DataType top(Heap* php) {
    assert(php);
    return php->a[0];
}

（五）其他操作

DataType top(Heap* php) {
    assert(php);
    return php->a[0];
}

bool empty(Heap* php) {
    assert(php);
    return php->size == 0;
}

size_t Size(Heap* php) {
    assert(php);
    return php->size;
}

void destroy(Heap* php) {
    free(php->a);
    php->capacity = php->size = 0;
}
// 交换两个变量值的辅助函数
void swap(DataType* a, DataType* b) {
    DataType temp = *a;
    *a = *b;
    *b = temp;
}

堆排序

（一）堆排序的基本思想

堆排序是一种基于堆数据结构的排序算法，它利用堆的性质来构建一个最大堆或最小堆，然后通过交换堆顶元素和堆尾元素来实现排序。

（二）堆排序的步骤

1. 构建最大堆。
2. 将堆顶元素与堆尾元素交换。
3. 堆的大小减一，重新调整堆。
4. 重复步骤 2 和 3，直到堆的大小为 1。

（三）堆排序的代码实现

void HeapSort(int* a, int n) {
    // 构建最大堆
    for (int i = (n - 1 - 1) / 2; i >= 0; i--) {
        AdjustDown(a, n, i);
    }
    int end = n - 1;
    while (end > 0) {
        swap(&a[end], &a[0]);
        AdjustDown(a, end, 0);
        end--;
    }
}

（四）堆排序的时间复杂度

堆排序的时间复杂度为 O(n log n)，其中 n 是数组的长度。构建最大堆的时间复杂度为 O(n)，每次调整堆的时间复杂度为 O(log n)，而总共需要进行 n-1 次调整。

例题

215. 数组中的第K个最大元素 - 力扣（LeetCode）

给定整数数组 nums 和整数 k，请返回数组中第 **k** 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4

我们可以利用堆的性质来解决这个问题，具体步骤如下：

1. 构建一个大小为 k 的小顶堆。
2. 遍历数组中的每个元素，如果元素大于堆顶元素，则将堆顶元素替换为该元素，并重新调整堆。
3. 最后，堆顶元素即为第 k 个最大的元素。

void swap(int* a, int* b) {
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

void AdjustDown(int* a, int n, int parent) {
    int child = 2 * parent + 1; 
    while (child < n) {

        if (child + 1 < n && a[child] > a[child + 1]) {
            child++;
        }

        if (a[parent] <= a[child]) {
            break;
        }
    
        swap(&a[parent], &a[child]);
  
        parent = child;
        child = 2 * parent + 1;
    }
}

int findKthLargest(int* nums, int numsSize, int k) {
    // 构建大小为 k 的小顶堆
    for (int i = (k - 1 - 1) / 2; i >= 0; i--) {
        AdjustDown(nums, k, i);
    }
    // 遍历数组中的每个元素
    for (int i = k; i < numsSize; i++) {
        if (nums[i] > nums[0]) {
            swap(&nums[i], &nums[0]);
            AdjustDown(nums, k, 0);
        }
    }
    return nums[0];
}

230. 二叉搜索树中第 K 小的元素 - 力扣（LeetCode）

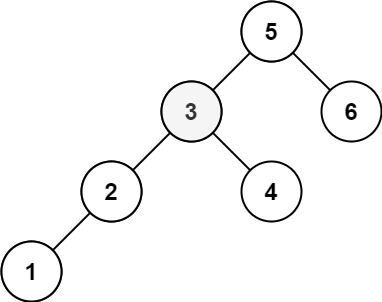
给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 小的元素（从 1 开始计数）。

示例 1：
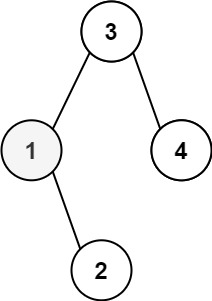
输入：root = [3,1,4,null,2], k = 1
输出：1
示例 2：
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3
提示：

树中的节点数为 n 。
1 <= k <= n <= 104
0 <= Node.val <= 104

二叉搜索树的中序遍历结果是一个递增序列，因此我们可以通过中序遍历来找到第 k 小的元素。

int kthSmallest(struct TreeNode* root, int k) {
    int* res = (int*)malloc(sizeof(int) * k);
    int idx = 0;
    struct TreeNode* stack[10000];
    int top = -1;
    struct TreeNode* node = root;
    while (node != NULL || top != -1) {
        while (node != NULL) {
            stack[++top] = node;
            node = node->left;
        }
        node = stack[top--];
        res[idx++] = node->val;
        if (idx == k) {
            break;
        }
        node = node->right;
    }
    int ans = res[k - 1];
    free(res);
    return ans;
}