PINN+贝叶斯=顶会顶刊！思路上升期，好发不卷

2024深度学习发论文&模型涨点之——PINN+贝叶斯

之前我们仔细介绍过PINN——多篇成果登上Nature及Science正刊的香饽饽。将贝叶斯方法和PINN结合，我们就能得到贝叶斯物理信息神经网络（B-PINNs）。B-PINNs利用贝叶斯框架，通过结合贝叶斯神经网络（BNN）和PINNs来解决具有噪声数据的非线性PDE问题。

最近PINN+贝叶斯也取得不少突破，Neurips、Nature子刊、ACM等顶会顶刊接连录用B-PINNs，况且目前这个方向还不算卷，没有思路的同学抓紧时间上车！

我整理了一些【B-PINNs】相关论文，需要的同学公人人人号【AI创新工场】自取

论文精选

论文1：

B-PINNs: Bayesian Physics-Informed Neural Networks for Forward and Inverse PDE Problems with Noisy Data

B-PINNs：贝叶斯物理信息神经网络用于具有噪声数据的正向和逆向偏微分方程问题

方法

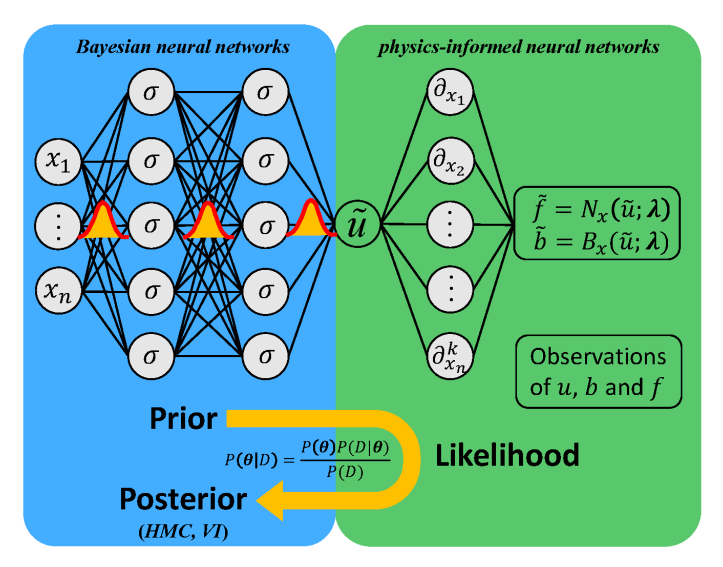
• 贝叶斯物理信息神经网络（B-PINNs）：结合贝叶斯神经网络（BNN）和物理信息神经网络（PINN）作为先验，使用哈密顿蒙特卡洛（HMC）或变分推断（VI）作为后验估计器。

• 贝叶斯框架：利用物理定律和分散的噪声测量数据，在贝叶斯框架内提供预测并量化由噪声数据引起的偶然不确定性。

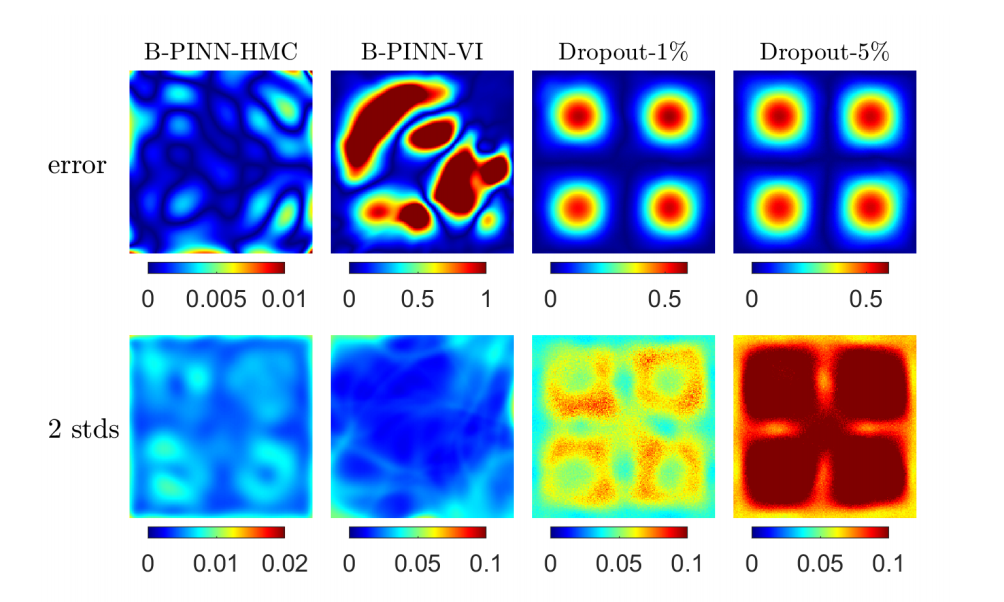
• 后验估计方法比较：系统比较了HMC和VI两种不同的B-PINNs后验估计方法，以及用于量化深度神经网络不确定性的dropout方法。

• 卡方-洛夫（KL）展开和深度归一化流（DNF）模型：将BNN替换为截断的KL展开，并结合HMC或DNF模型作为后验估计器。

创新点

• 贝叶斯框架的引入：在PINNs中引入贝叶斯框架，提供了不确定性量化的功能，并在大噪声场景下通过避免过拟合获得更准确的预测。

• B-PINNs后验估计方法的系统比较：首次系统比较了HMC和VI在B-PINNs后验估计中的适用性，以及dropout方法在不确定性量化中的局限性。

• KL展开和DNF模型的应用：提出了使用KL展开和DNF模型作为B-PINNs后验估计器的新方法，这些方法在准确性和计算效率上具有优势，但限于低维问题。

  

论文2：

Correcting model misspecification in physics-informed neural networks (PINNs)

纠正物理信息神经网络（PINNs）中的模型误设定

方法

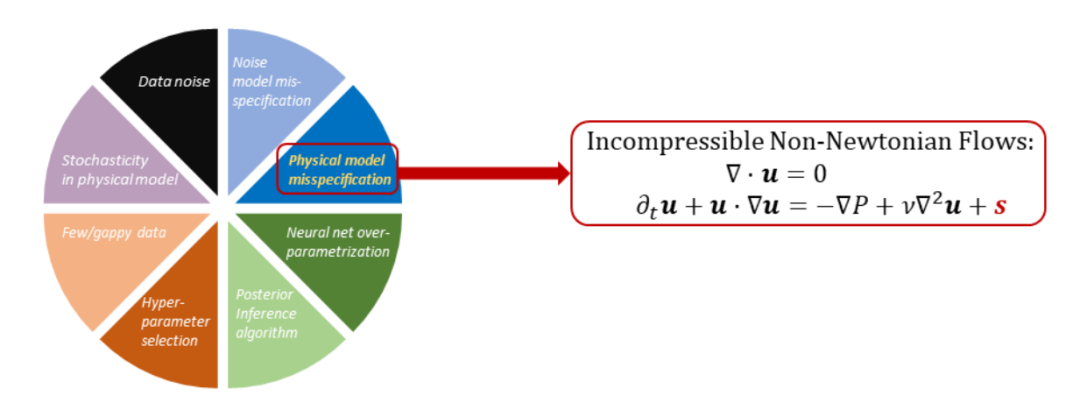
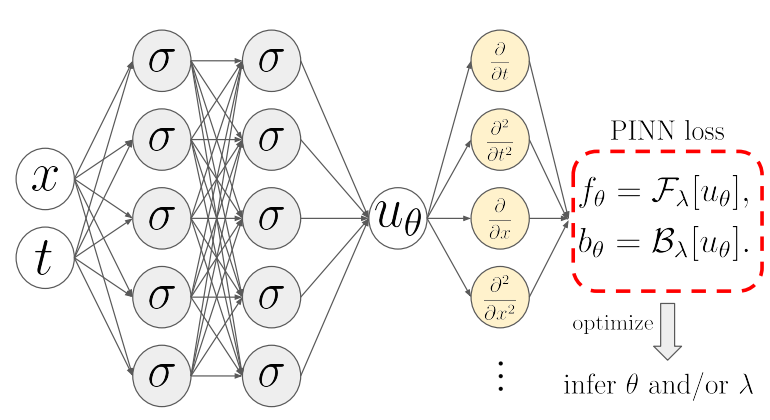
• 模型误设定的纠正：提出一种通用方法，通过在PINNs中添加深度神经网络（DNNs）来纠正可能的模型误设定。

• 贝叶斯物理信息神经网络（B-PINNs）和集成PINNs：用于量化由噪声和/或不完整数据引起的不确定性。

• 符号回归的结合：展示了如何将提出的方法与符号回归结合，以在PINNs训练后获得明确的控制方程。

创新点

• 模型误设定的识别与纠正：在PINNs中首次提出识别和纠正模型误设定的方法，增强了PINNs在复杂系统中的应用能力。

• 不确定性的量化：通过B-PINNs和集成PINNs提供了一种量化模型不确定性的方法，这对于处理噪声和不完整数据至关重要。

• 符号回归的整合：提出了一种将机器学习模型与符号回归相结合的新方法，以从数据中提取显式的控制方程，增强了模型的解释性和适用性。

论文3：

Error-Aware B-PINNs: Improving Uncertainty Quantification in Bayesian Physics-Informed Neural Networks

误差感知B-PINNs：提高贝叶斯物理信息神经网络中的不确定性量化

方法

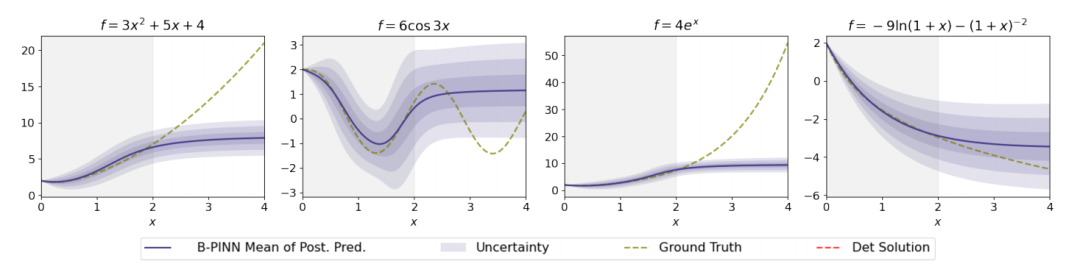
• 贝叶斯物理信息神经网络（B-PINNs）：提出了一个框架，用于在B-PINNs中纳入B-PINN解决方案与未知真实解决方案之间的差异。

• 误差感知B-PINNs：引入了误差感知B-PINNs的概念，并考虑了预测方差中的伪随机不确定性。

• 残差网络（rθ(x)）：定义了一个残差网络，与uθ(x)共享参数，理想情况下对于任何输入x ∈ Ω，其输出应为零。

• 贝叶斯神经网络（BNNs）：使用贝叶斯框架进行不确定性量化，通过贝叶斯推断为参数θ赋予概率分布。

• 预测分布估计：通过积分或蒙特卡洛估计来近似预测分布p(ˆy|x,O)。

创新点

• 误差感知B-PINNs：提出了误差感知B-PINNs，通过增加有用的误差估计来改善预测质量，特别是在模型未训练的区域。

• 伪随机不确定性：引入了伪随机不确定性来量化u和uθ之间的差异，提高了不确定性估计的可靠性。

• 线性动态系统的应用：在一类线性动态系统上验证了误差感知B-PINNs的概念，并能严格建模伪随机不确定性。

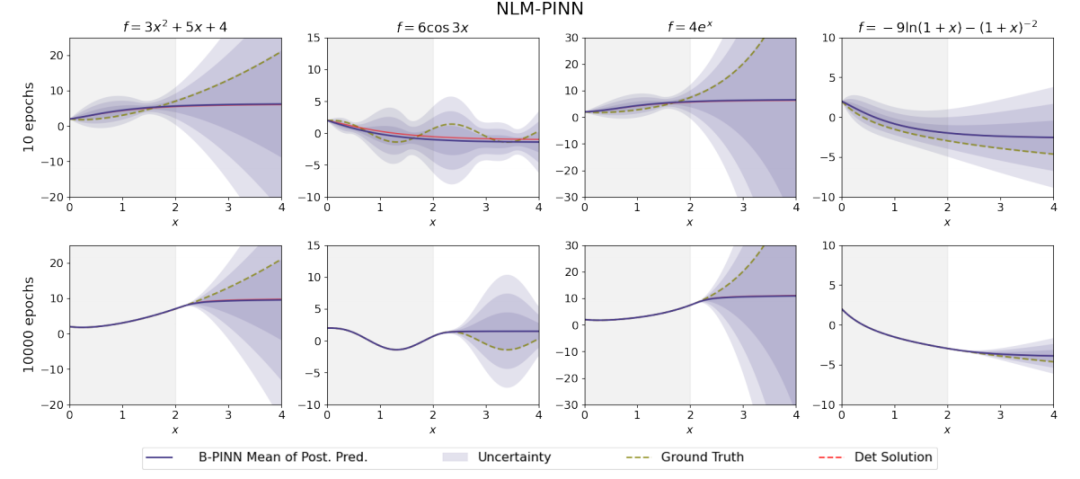
• 与Neural Linear Model (NLM)的结合：展示了如何将误差感知B-PINNs与NLM结合，以保持封闭形式解的存在，并允许先验优化。

论文4：

Improvement of Bayesian PINN Training Convergence in Solving Multi-scale PDEs with Noise

提高贝叶斯PINN在解决带噪声的多尺度偏微分方程中的训练收敛性

方法

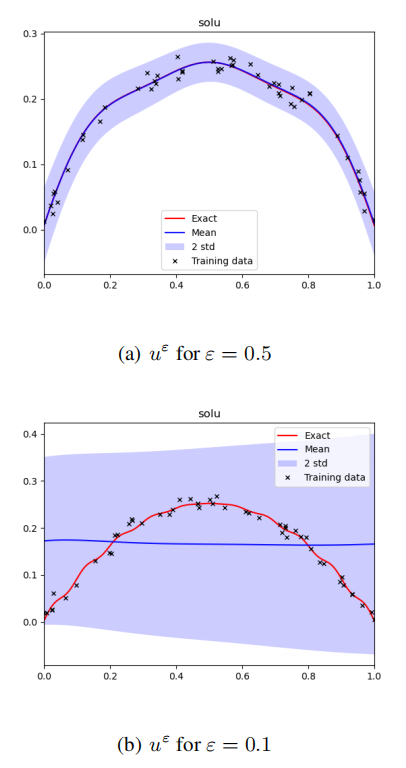
• 贝叶斯物理信息神经网络（BPINN）：利用贝叶斯统计学来估计PINN参数，并将似然函数纳入考虑。

• 汉密尔顿蒙特卡洛（HMC）：用于BPINN的后验采样，通过解决汉密尔顿系统来生成新的步骤。

• 随机梯度下降（SGD）：将SGD重新框架为HMC，以确保始终提供最“可能”的估计。

• 多尺度深度神经网络（MscaleDNN）：通过傅里叶特征映射（FFM）增强DNN，以改善对高频成分的表示。

创新点

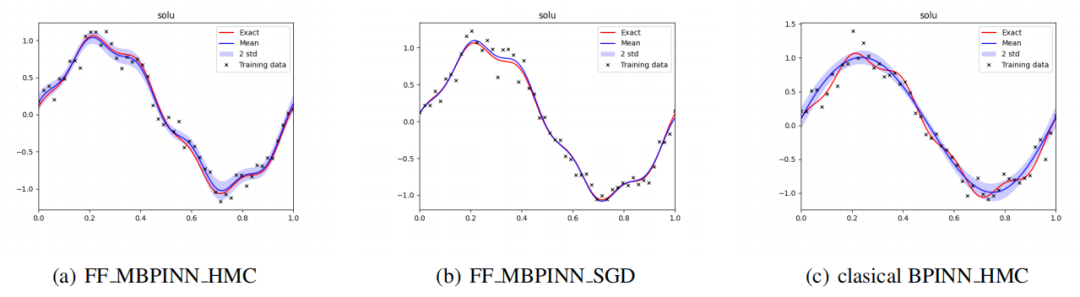
• MBPINN方法：通过整合MscaleDNN和贝叶斯推断，提出了一种新的MBPINN方法，提高了对多尺度PDE的适用性。

• SGD重新框架HMC：提出了一种新的估计方法，通过SGD重新框架HMC来解决传统HMC的收敛问题。

• 傅里叶特征映射（FFM）：通过FFM增强DNN，提高了网络对高频成分的学习能力，从而改善了对复杂问题的解决能力。

• 灵活性和计算成本：MBPINN方法比HMC更灵活，计算成本更低，特别是在处理复杂PDE问题时。