第九章作业

习题9.2

import numpy as np
from scipy.stats import shapiro

# 给定数据
data = np.array([15.0, 15.8, 15.2, 15.1, 15.9, 14.7, 14.8, 15.5, 15.6, 15.3,
                 15.1, 15.3, 15.0, 15.6, 15.7, 14.8, 14.5, 14.2, 14.9, 14.9,
                 15.2, 15.0, 15.3, 15.6, 15.1, 14.9, 14.2, 14.6, 15.8, 15.2,
                 15.9, 15.2, 15.0, 14.9, 14.8, 14.5, 15.1, 15.1, 15.5, 15.5,
                 15.1, 15.0, 15.3, 15.7, 14.5, 15.5, 15.0, 15.7, 14.6, 14.2])

# 样本均值和标准差
sample_mean = 15.0780
sample_std = 0.4325

# 进行Shapiro - Wilk检验
statistic, p_value = shapiro(data)
print("Shapiro - Wilk statistic:", statistic)
print("p - value:", p_value)

if p_value > 0.05:
    print("The data is normally distributed.")
else:
    print("The data is not normally distributed.")

运行结果

习题9.3-1

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 数据
data = np.array([
    [4.13, 3.86, 4.00, 3.88, 4.02, 4.00],
    [4.07, 3.85, 4.02, 3.88, 3.95, 3.86],
    [4.04, 4.08, 4.01, 3.91, 4.02, 3.96],
    [4.07, 4.11, 4.01, 3.95, 3.89, 3.97],
    [4.05, 4.08, 4.04, 3.92, 3.91, 4.00],
    [4.04, 4.01, 3.99, 3.97, 4.01, 3.82],
    [4.02, 4.02, 4.03, 3.92, 3.89, 3.98],
    [4.06, 4.04, 3.97, 3.90, 3.89, 3.99],
    [4.010, 3.97, 3.98, 3.97, 3.99, 4.02],
    [4.05, 3.95, 3.98, 3.90, 4.00, 3.93]
]).T

# 选择前面6列数据，通过切片操作 [:, :6] 选取
selected_data = data[:, :6]

# 创建DataFrame，指定6个列名
df = pd.DataFrame(selected_data, columns=['Lab1', 'Lab2', 'Lab3', 'Lab4', 'Lab5', 'Lab6'])

# 绘制箱线图
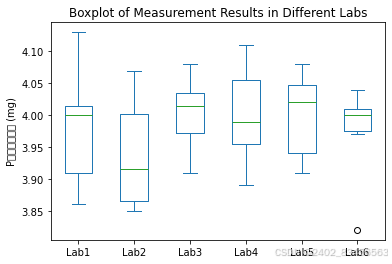
df.plot.box()
plt.title('Boxplot of Measurement Results in Different Labs')
plt.ylabel('P尔敏有效含量 (mg)')
plt.show()

运行结果

习题9.3-2

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import f_oneway

data = np.array([
    [4.13, 3.86, 4.00, 3.88, 4.02, 4.00],
    [4.07, 3.85, 4.02, 3.88, 3.95, 3.86],
    [4.04, 4.08, 4.01, 3.91, 4.02, 3.96],
    [4.07, 4.11, 4.01, 3.95, 3.89, 3.97],
    [4.05, 4.08, 4.04, 3.92, 3.91, 4.00],
    [4.04, 4.01, 3.99, 3.97, 4.01, 3.82],
    [4.02, 4.02, 4.03, 3.92, 3.89, 3.98],
    [4.06, 4.04, 3.97, 3.90, 3.89, 3.99],
    [4.010, 3.97, 3.98, 3.97, 3.99, 4.02],
    [4.05, 3.95, 3.98, 3.90, 4.00, 3.93]
]).T

# 通过切片获取前7列数据作为不同组
lab1 = data[:, 0]
lab2 = data[:, 1]
lab3 = data[:, 2]
lab4 = data[:, 3]
lab5 = data[:, 4]
lab6 = data[:, 5]
lab7 = data[:, 6]

# 进行方差分析
f_statistic, p_value = f_oneway(lab1, lab2, lab3, lab4, lab5, lab6, lab7)
print("F - statistic:", f_statistic)
print("p - value:", p_value)

if p_value < 0.05:
    print("There is a significant difference in the means.")
else:
    print("There is no significant difference in the means.")

运行结果

习题9.4

import numpy as np
from scipy.stats import f_oneway

# 产量数据
yield_data = np.array([
    [173, 172, 173],
    [174, 176, 178],
    [177, 179, 176],
    [172, 173, 174],
    [175, 173, 176],
    [178, 177, 179],
    [174, 175, 173],
    [174, 174, 175],
    [177, 175, 176],
    [174, 174, 175],
    [170, 171, 172],
    [169, 169, 170]
])

# 分别提取各因素水平的数据
A1_yield = yield_data[0:4].flatten()
A2_yield = yield_data[4:8].flatten()
A3_yield = yield_data[8:12].flatten()
B1_yield = yield_data[0:3]
B2_yield = yield_data[3:6]
B3_yield = yield_data[6:9]
B4_yield = yield_data[9:12]

# 对品种A进行单因素方差分析
f_A, p_A = f_oneway(A1_yield, A2_yield, A3_yield)
print("For factor A (wheat variety):")
print("F - statistic:", f_A)
print("p - value:", p_A)

# 对化肥B进行单因素方差分析
f_B, p_B = f_oneway(B1_yield.flatten(), B2_yield.flatten(), B3_yield.flatten(), B4_yield.flatten())
print("For factor B (fertilizer type):")
print("F - statistic:", f_B)
print("p - value:", p_B)

运行结果

习题9.5

import numpy as np
import statsmodels.api as sm
from statsmodels.formula.api import ols
import pandas as pd  # 添加这行代码，导入pandas库并使用pd作为别名

# 销售量数据
sales_data = np.array([
    [955, 967, 960, 950],
    [927, 949, 950, 940],
    [905, 930, 920, 910],
    [855, 860, 880, 875],
    [880, 890, 895, 900],
    [860, 840, 850, 830],
    [870, 865, 850, 860],
    [830, 850, 840, 830],
    [875, 888, 900, 892],
    [870, 850, 847, 965],
    [870, 863, 845, 855],
    [821, 842, 832, 848]
])

# 将数据转换为适合statsmodels的格式
sales_data_reshaped = sales_data.reshape(-1, 1)
factors = np.array([
    [1, 1, 1], [1, 1, 2], [1, 2, 1], [1, 2, 2],
    [2, 1, 1], [2, 1, 2], [2, 2, 1], [2, 2, 2],
    [3, 1, 1], [3, 1, 2], [3, 2, 1], [3, 2, 2]
] * 4)
df = sm.add_constant(np.hstack((factors, sales_data_reshaped)))
df = pd.DataFrame(df, columns=['const', 'A', 'B', 'C', 'sales'])

# 再次明确将A、B、C列转换为category类型
df['A'] = df['A'].astype('category')
df['B'] = df['B'].astype('category')
df['C'] = df['C'].astype('category')

# 进行三因素方差分析
model_with_one_interaction = ols('sales ~ C(A) + C(B) + C(C) + C(A):C(B)', data=df).fit()
anova_table_with_one_interaction = sm.stats.anova_lm(model_with_one_interaction, typ=2)
print(anova_table_with_one_interaction)