C语言实现数据结构：堆排序和二叉树_链式

---

一.堆的应用

1.堆排序

void test01()
{
	int arr[] = { 17,20,10,13,19,15 };
	int n = sizeof(arr) / sizeof(arr[0]);

	HP p;
	HPInit(&p);

	for (int i = 0; i < n; i++)
	{
		HPPush(&p, arr[i]);
	}
	int i = 0;
	while (!HPEmpty(&p))
	{
		arr[i++] = HPTop(&p);
		HPPop(&p);
	}

	for (int i = 0; i < n; i++)
	{
		printf("%d ", arr[i]);
	}

	HPDesTroy(&p);
}

但是真正的堆排序不是我们上面这种写法，堆排序是借助堆的算法思想，而不能够直接使用堆的数据结构来辅助实现，这个时候我们来看一看怎么来实现堆的排序。

首先先将这三个我之前写的算法放到我们头文件里，可以用来直接使用。

void Swap(int* x, int* y);
void AdjustUp(HPDataType* arr, int child);
void AdjustDown(HPDataType* arr, int parent, int n);

(1)向下调整算法建堆的堆排序

我们建的是小堆

void HeapSort(int* arr, int n)
{
	//向下调整算法建堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(arr, i, n);
	}

	int end = n - 1;
	while (end)
	{
		Swap(&arr[0], &arr[end]);
		AdjustDown(arr, 0, end);
		end--;
	}
}

测试

建的是小堆，排的是降序的数组。所以排升序建大堆，排降序建小堆。

向下调整算法的最差的时间复杂度为O(logn)。
所以向下调整算法建堆的时间复杂度为：O(n×log n)。
总的来说，向下调整堆排序的时间复杂度就为：O(nlogn)。

(2)向上调整算法建堆的堆排序

我们这次来建一个大堆

	//向上调整算法建堆
	for (int i = 0; i < n; i++)
	{
		AdjustUp(arr, i);
	}

	int end = n - 1;
	while (end)
	{
		Swap(&arr[0], &arr[end]);
		AdjustDown(arr, 0, end);
		end--;
	}

测试

向上调整算法最差的时间复杂度为：O(log n)。
向上调整算法建堆的时间复杂度：O(nlogn)
向上调整堆排序的时间复杂度：O(nlogn)。

我们通过总结得：向下调整算法建堆的时间复杂度比较好，越向下，结点个数逐渐增多，向下调整次数逐渐减少。向上调整算法建堆刚好相反。

---

二.实现链式结构二叉树

用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址，其二叉树结点结构的定义如下：

1.二叉树结点结构的定义

typedef int BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

代码实现

构造一棵二叉树，将数据类型转化成char。

2.获取一个新结点

BTNode* buyNode(BTDataType x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
		perror("molloc fail!");
		exit(1);
	}

	newnode->data = x;
	newnode->left = newnode->right = NULL;

	return newnode;
}

3.手动构造一棵二叉树

BTNode* CreateTree()
{
	BTNode* nodeA = buyNode('A');
	BTNode* nodeB = buyNode('B');
	BTNode* nodeC = buyNode('C');
	BTNode* nodeD = buyNode('D');
	BTNode* nodeE = buyNode('E');
	BTNode* nodeF = buyNode('F');


	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;

	return nodeA;

}

4.前序遍历

void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	printf("%c ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);

}

测试

5.中序遍历

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	InOrder(root->left);
	printf("%c ", root->data);
	InOrder(root->right);


}

测试

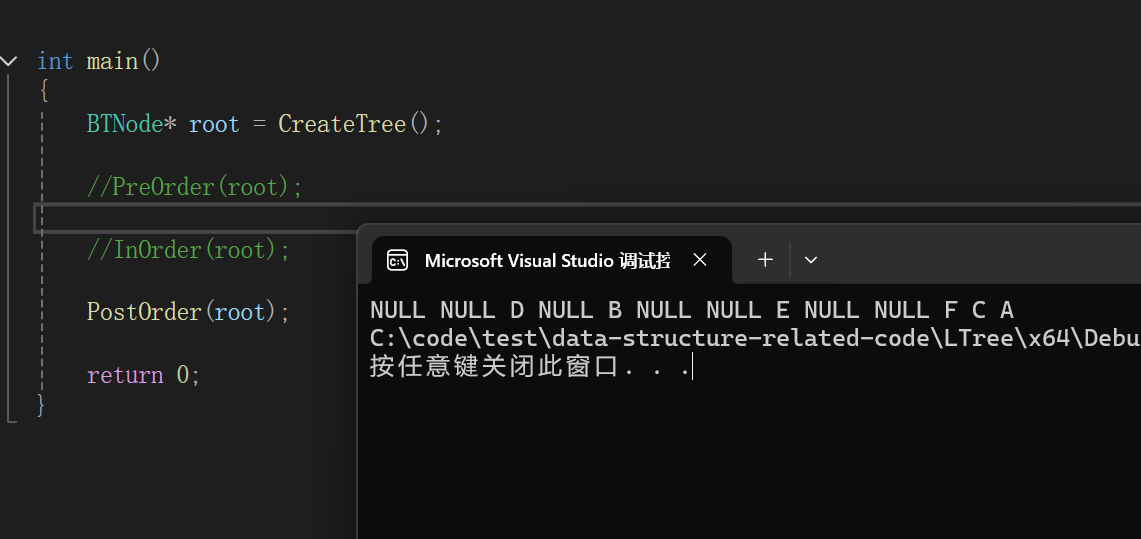
6.后序遍历

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->data);
}

测试

7.二叉树结点个数

int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

8.二叉树叶子结点个数

int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}

	return BinaryTreeLeaft(root->left) + BinaryTreeLeaft(root->right);
}

9.二叉树第k层结点个数

int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}

	if (k == 1)
	{
		return 1;
	}

	return BinaryTreeLevelKSize(root->left,k-1) + BinaryTreeLevelKSize(root->right,k-1);
}

10.二叉树的深度/高度

int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	int leftDep = BinaryTreeDepth(root->left);
	int rihgtDep = BinaryTreeDepth(root->right);

	return 1 + (leftDep > rihgtDep ? leftDep : rihgtDep) ;
}

11.二叉树查找值为x的结点

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}

	if (root->data == x)
	{
		return root;
	}

	BTNode* leftFind = BinaryTreeFind(root->left,x);
	if (leftFind)
	{
		return leftFind;
	}

	BTNode* rightFind = BinaryTreeFind(root->right,x);

	if (rightFind)
	{
		return rightFind;
	}

	return NULL;
}

12.二叉树销毁

void BinaryTreeDestroy(BTNode** root)
{
	if (*root == NULL)
	{
		return;
	}

	BinaryTreeDestroy(&((*root)->left));
	BinaryTreeDestroy(&((*root)->right));
	free(*root);
	*root = NULL;
}