食物链(三类动物)

用一个relation[]来存储关系，0代表同类，1代表吃父节点，2代表被父节点吃。将其想象成一棵树，这些动物相当于树上的不同节点，则他们之间必定有某种关系，即上面的0，1，2。

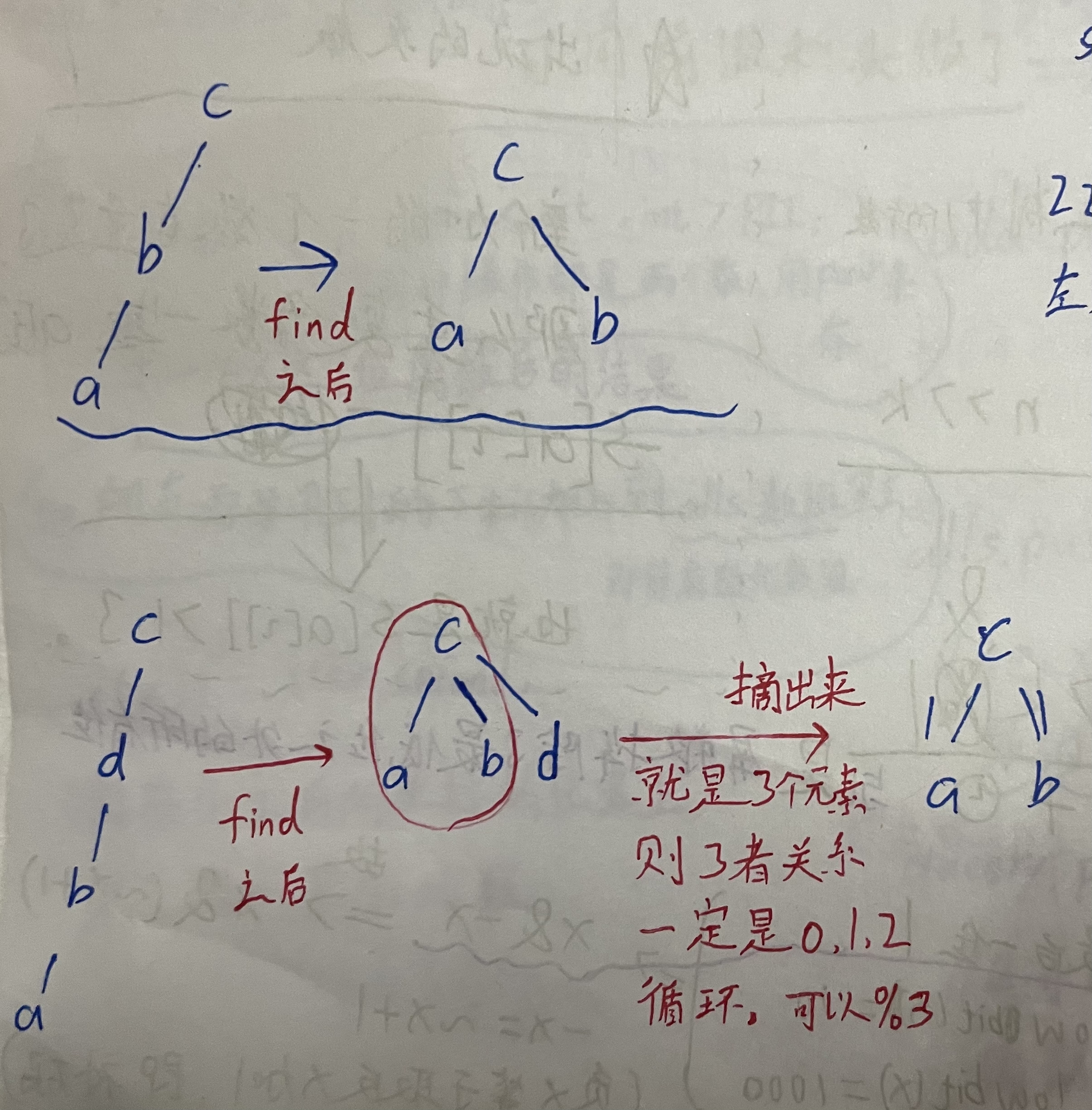
我们利用并查集中的find函数，在将树中每个节点的父节点指向根节点的同时，更新其与根节点的关系。

这样的话，我们示例验证a和b是否是同类：1.判断根节点是否相同。2.a和b与根节点的关系是否相同。若1，2皆满足则a和b一定相同。

或者我们根据所描述的a和b是同类，来进行更新节点的父节点的操作，同时更新节点的relation[]的操作（父节点变了，relation[]一定要更新）。

1.把a的父节点指向b的父节点（ p[find(a) ]=find(b) )。

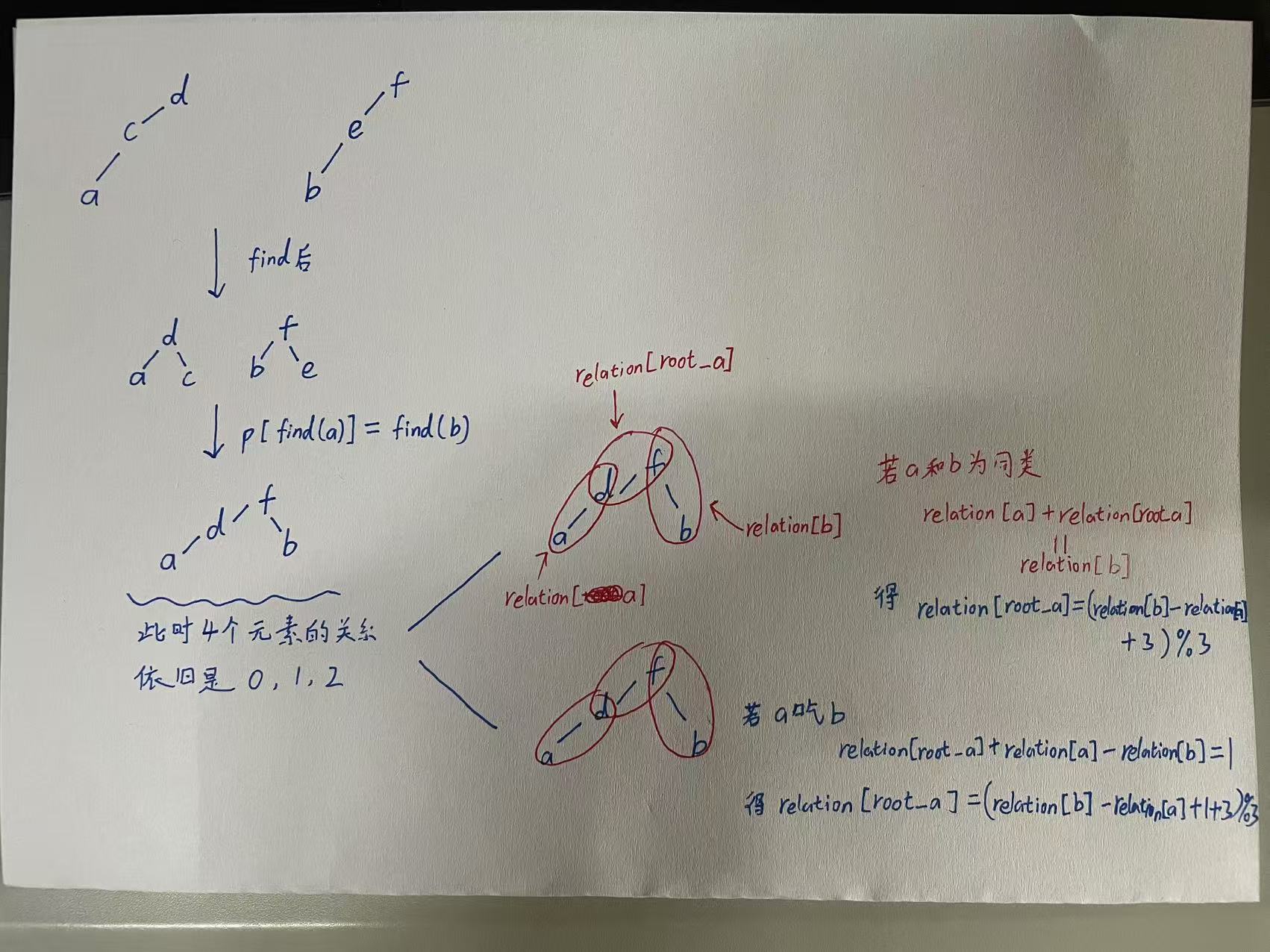
2.有relation[a] + relation[root_a] = relation[b],上面的等式是我们根据a和b是同类推出来的，root_a的代表是a原先的父节点，且只有relation[root_a]是未知的，于是就有

relation[root_a]=(relation[b]-relation[a]+3)%3

#include<iostream>
using namespace std;

const int M = 1e5 + 10;

int N, K;
int p[M], relation[M];//p为父节点数组，relation是与父节点的关系数组
int temp;

int find(int x)
{
	if (p[x] != x)
	{
		int old_p = p[x];
		p[x] = find(p[x]);
		relation[x] = (relation[x] + relation[old_p]) % 3;//路径压缩时更新关系
	}
	return p[x];
}

int main()
{
	scanf_s("%d%d", &N, &K);
	//初始化
	for (int i = 1; i <= N; i++)
	{
		p[i] = i;//开始时每个节点的父节点是它本身
		relation[i] = 0;//自己是自己的同类
	}
	int D, a, b;
	
	while (K--)
	{
		scanf_s("%d%d%d", &D, &a, &b);
		//检查输入是否越界
		if (a > N || b > N)                        //要加continue，跳出当前循环，进行下一次循环
		{
			temp++;
			continue;
		}

		int root_a = find(a);
		int root_b = find(b);

		if (D == 1)//说a和b时同类，接下来验证真假，或者根据这句话更新a和b的关系
		{
			if (root_a == root_b)
			{
				if (relation[a] != relation[b])temp++;
			}
			else
			{
				p[find(a)] = find(b);//更新a的父节点
				relation[root_a] = (relation[b] - relation[a] + 3) % 3;//得到a原来的祖先节点到他们新的祖先节点的关系
			}
		}
		if (D == 2)//说a吃b
		{
			if (a == b)//自己不能吃自己
			{
				temp++;
				continue;//依旧不能漏掉continue
			}
			if (root_a == root_b)
			{
				if ((relation[a] - relation[b] + 3) % 3 != 1)temp++;//判断a是否吃b，即差值模三是否为1
			}
			else
			{
				p[find(a)] = find(b);//更新a的父节点
				relation[root_a] = (relation[b] - relation[a] + 1 + 3) % 3;
			}
		}

	}
	printf("%d\n", temp);
	return 0;
}

acwing240 算法打卡，属于并查集的运用