素数判断（4种方法，由简到难）

DW_DROME

已于 2024-11-03 12:12:10 修改

阅读量4.2k

点赞数 15

文章标签：算法数据结构

于 2024-10-21 23:28:19 首次发布

本文链接：https://blog.csdn.net/2402_87385120/article/details/143134187

版权

1. 最简单方法时间复杂度（根号n）

bool isPrime(int n){ //simple
    if(n<=1)
        return false;
    for (int i = 2; i * i <= n;i++){
        if(n%i==0)
            return false;
    }
    return true;
}

2. 埃拉托色尼筛法（sieve of Eratosthenes）时间复杂度（nloglogn）

经典质数筛法、小范围

思想：

通过首先标记合数，剩下的就都是质数了；

难点：

合数标记：从i=2开始，若i为质数，那么i^2一定不是质数。接着是i=3、i=4
优化起点：为什么从i^2开始标记？因为比i^2小的数之前已被标记了。

void sieveOfEratosthenes(int n){//The function name was found on the internet,don't worried.
    vector<bool> isPrime(n + 1, true);
    isPrime[0] = isPrime[1] = false;
    for (int i = 2; i * i <= n;i++){
        if(isPrime[i]){
            for (int j = i * i; j<= n; j += i)
            {
                isPrime[j] = false;
            }
        }
    }
    //From 2 to larger number,the function firstly scanfs the Non-prime number.
}

用isprime储存质数，之后再记录由指数因构成的合数。加快筛法速度。

3.欧拉函数时间复杂度 n

是埃拉托色尼筛法的改良版。

思想：

欧拉函数的定义

小于或等于n 且与n互质的正整数的个数

难点：

[质因数的分解] --》欧拉函数的计算基于n的质因数分解。（于是我们可以倒过来）

if n 能被质数p 整除，说明n与p的倍数都不互质。

[公式推导]

对于n的每一个质因数p，减少n/p的部分。

比如说 = n(1-1/p1)(1-1/p2) ……

比说是n=36 = 36(1-1/2)(1-1/3)=12 ----->小于等于36的质数有12个

int eulerTotient(int n){
    int result = n;
    for (int i = 2; i * i <= n;i++){
        if(n%i==0){
            while(n%i==0)
                n /= i;
            result -= result / i;
        }
    }
    if(n>1)
        result -= result / n;
    return result;
}

以上都是基于欧拉函数的基本思想。于是我们可以倒退过来，设立一个isprime，这样就可以检查之前的指数因是否能够推出这个数了！

bool euler_sieve(int n){
    if (n < 2){
        return false;
    }

    vector<int> primes;                
    vector<bool> isPrime(n + 1, true); 
    isPrime[0] = isPrime[1] = false;  

    for (int i = 2; i <= n; ++i){
        if (isPrime[i]){
            primes.push_back(i); // If prime, add it 
        }
        // Mark multiples of i as non-prime
        for (int j = 0; j < primes.size() && i * primes[j] <= n; ++j){
            isPrime[i * primes[j]] = false; // Mark i * primes[j] as non-prime
            if (i % primes[j] == 0)         // find if founded
                break; 
        }
    }

    // Check if the number n is prime
    if (isPrime[n])
        return true;
    else
        return false;
}

欧拉筛相比于埃筛有一个进步点，那就是多了一个primes用于保存当前的素数，

如30.

埃	欧
2 被标记为2*15	2标记为2*15
3 被标记为3*10	3时，会先遍历primes，然后跳过
5 被标记为5*6

3 分段函数（Segmented Sieve）

———适合大范围（较大），

思想：

分而治之

难点：

使用简单筛法，找到2->根号r 内的所有质数，做为更大范围合数的因子
用小银子寻找 [l,r] 内的合数使用埃思想，存在优化空间，期待读者优化。
起始点(不错过任何一个合数)： int start = max(i*i,(l+i-1)/i)*i 注意是字母l。

vector<int> simpleSieve(int n){
    vector<int> primes;
    vector<bool> isPrime(n + 1, true);
    isPrime[0] = isPrime[1] = false;

    for (int i = 2; i <= n; ++i){
        if (isPrime[i])
            primes.push_back(i); // If prime, add it 
        for (int j = 0; j < primes.size() && i * primes[j] <= n; ++j){
            isPrime[i * primes[j]] = false; 
            if (i % primes[j] == 0)         // Break if i is divisible by primes[j]
                break;
        }
    }
    return primes;
}
void segmentedSieve(int l, int r)
{
    // Ensure l starts at 2 or above
    if (l < 2)
        l = 2;

    int limit = floor(sqrt(r)) + 1;
    vector<int> primes = simpleSieve(limit);
    vector<bool> isPrime(r - l + 1, true); 

    for (int i : primes){
        int start = max(i * i, ((l + i - 1) / i) * i);

        for (int j = start; j <= r; j += i)
            isPrime[j - l] = false; 
    }
}

为什么要max，因为当 i*i在这个区间的时候，可以直接用，但是不在的时候，比如说>r 了，就不能直接使用了，需要在区间内找到第一个大于等于 l 的 i 的倍数

为什么要 /i）*i 为了向上取整。

4.miller-rabin质数测试

——一种概率质数测试算法（我只能说会写代码，至于原理不怎么懂，好难）

思想：

快速检查一个数是否是质数，for > 10的18次方。适用于超超大数的判断（可能错误）

难点：

[幂模运算] ~> 快速幂 ~> a的r次方 mod n 时间复杂度 logr
[质数检测逻辑] ~> 费马小定理

即如果 p 是一个素数，并且 a 是一个小于 p 且与 p 互质的整数（也就是 a 和 p 之间没有公因数），那么有：

也就是说，若 p 是素数，且 a 是与 p 互质的数，那么 a^(p-1) 除以 p 的余数是 1。

[增加测试次数] 使用interations 参数来控制轮次，提高正确率。

还是难以理解？这是我的笔记，希望对你有帮助！

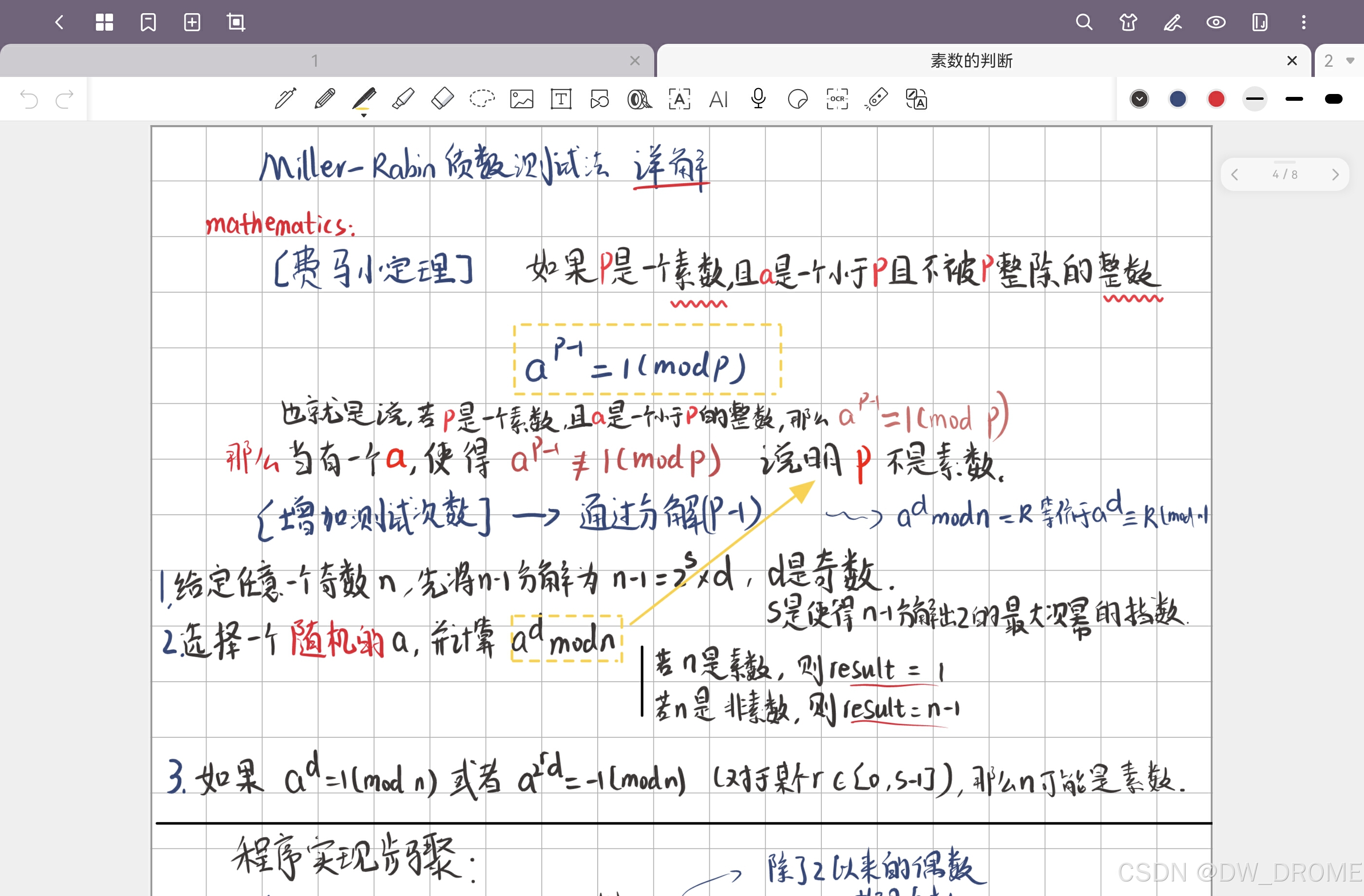
如果你对这个数学式子的格式有问题。以下解释了：

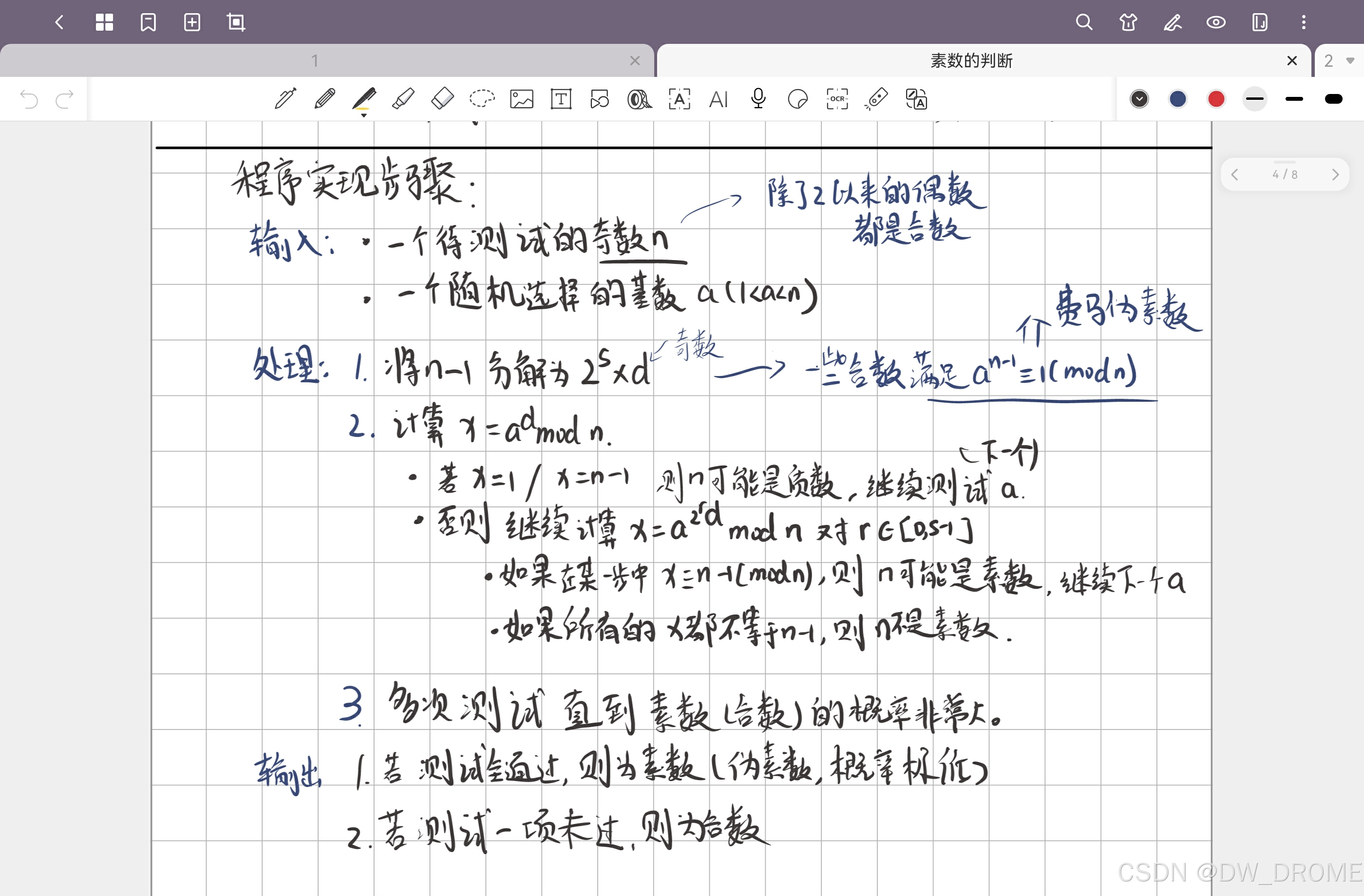
代码（因为过于复杂了，所以这个我使用中文注释）

// 幂次模运算函数，计算 a^r % n
int power(int a, int r, int n){
    int result = 1;  // 初始化结果为1
    a = a % n;  // 预处理 a 的模 n 值，避免过大
    while (r > 0){  // 当 r > 0 时，进行循环
        if (r % 2 == 1)  // 如果 r 是奇数，则将当前 a 的值乘入结果
            result = (result * a) % n;  // 更新 result，模 n 运算
        r = r >> 1;  // r 右移一位，相当于 r = r / 2
        a = (a * a) % n;  // 将 a 的平方并模 n
    }
    return result;  // 返回 a^r % n 的结果
}

// Miller-Rabin 质数测试函数，参数为 n（待检测数）和 iterations（测试的迭代次数）
bool millerRabin(int n, int iterations){
    if (n < 2)  // 如果 n 小于 2，则不是素数
        return false;

    // 将 n-1 表示为 2^s * d 的形式，r 是 n-1，不断除以2
    int r = n - 1;
    while (r % 2 == 0)  // r 是偶数时，继续除以 2
        r /= 2;

    // 进行指定次数的迭代测试
    for (int i = 0; i < iterations; i++){
        // 随机选择 a，范围在 [2, n-2] 之间
        int a = 2 + rand() % (n - 4);

        // 计算 x = a^r % n
        int x = power(a, r, n);
        int temp = r;

        // 如果 x == 1 或 x == n-1，则继续下一次迭代
        if (x == 1 || x == n - 1)
            continue;

        // 检查是否为合数
        bool composite = true;
        // 重复平方，检查 x 是否等于 n-1
        while (temp != n - 1){
            x = (x * x) % n;  // 更新 x = x^2 % n
            temp *= 2;  // temp = temp * 2

            // 如果 x == 1，则 n 不是素数
            if (x == 1)
                return false;

            // 如果 x == n-1，则 n 可能是素数
            if (x == n - 1){
                composite = false;  // 不是合数，继续进行测试
                break;
            }
        }

        // 如果所有测试都未找到 n 是素数的证据，则 n 是合数
        if (composite)
            return false;
    }

    // 如果所有测试通过，返回 n 是素数
    return true;
}

额外补充

1 错误率分析：

对某个合数，某个（一个）a 可使得测试失败的概率通常小于1/4
所以，多次此时（10次）就可以极限的降低错误率 ~>(1/4)^k;

2伪素数？可靠吗？

有错误率分析，这算法十分可靠，可以高效地进行大整数的素性检测

3背后的数学原理

[二次剩余性质]：对于素数p来说，任何一个a满足那么p一定不是素数

我们可以用这个进一步优化miller-rabin的检测过程(质数和模运算result)->有效识别那些长得很像素数的合数。

4应用：

广泛应用在加密领域（RSA 加密）

一些关于二次剩余性质的补充

2024/11/2 针对miller-rabin素性测试的额外补充

在看了评论之后，意识到我一开始的文章非常不清晰，所以这里进行一些程序实现的具体思路

请看第二个式子，因为我们这里需要的条件是任意一个素数p和任意一个整数a

$a^{p-1}\equiv1\quad(\mathrm{mod}\, p)^{[1]}$

--倘若a是p的倍数（第三个式子），则a一定是大于等于p的。显然，我们这里没有这样的范围要求。

但是因为费马小定理的逆序述不成立，即素数满足这个条件，但满足这个条件的不一定是素数。

因此我们需要进行一些改动，即miller-rablin素性检测。

miller-rablin素性检测并不直接找到 p （即质数因），而是通过不断的幂次模运算来推断n是否是一个素数。

方法是：

1.由于二次剩余性质[二次剩余-OI Wiki],我们可以对n-1进行开平方处理

先将 n-1 分解为：

$n-1=2^s\cdot d$ 其中 d 是一个奇数，在程序的平方链中，temp = d .

2.随机选中一个a，[2,n-2]中

3.计算x初始值

$x = a^d \, (\mathrm{mod} \, n)$

4. 判断 x 是否合法，合法就进入下一个a，不合法就进入平方链。条件是

$x\equiv1(\mathrm{mod}\, n)$ $x\equiv n-1(\mathrm{mod}\, n)$

5.不合法就进入平方链中

先计算 $x=x^2(\mathrm{mod}\, n)$ ,获得x的新值

然后判断：

若 $x\equiv n-1(\mathrm{mod}\, n)$ 则n可能是素数，进入下一个循环

若 $x\equiv1(\mathrm{mod}\, n)$ 则n为合数

一些疑点？

第一个：这里设计到的初始计算 $x\equiv1(\mathrm{mod}\, n)$ ，则推断n为素数

但在平方链中 $x\equiv1(\mathrm{mod}\, n)$ ，却认为n为合数。

在初始计算中满足这一条件，其实是满足了费马小定理第二条通用公式。因而可以推断出n是素数，接着用下一个a来提高推断的可能性。

而在平方链中，我们需要提出来一个概念【非平凡的平方根】

定义：

对于模 n，一个非平凡的平方根是指一个整数 x，满足 $x^2\equiv1(\mathrm{mod}\, n)$ ，
但并不满足 $x\not\equiv\pm1$

意义：

对于 素数 n，只有 $x^2\equiv1(\mathrm{mod}\, n)$ 和 $x^2\equiv n-1(\mathrm{mod}\, n)$ 是 $x^2\equiv1(\mathrm{mod}\, n)$ 的解。
如果存在非平凡的平方根，说明 n 有因子，可以分解，因而是合数。