基于Matlab的四旋翼无人机动力学PID控制仿真，具体内容包括：-CSDN博客

本文链接：https://blog.csdn.net/2501_90314346/article/details/147468032

基于Matlab的四旋翼无人机动力学PID控制仿真，具体内容包括：

运用欧拉方程对地面坐标到机体坐标的转换矩阵进行了推导
在无人机动力学模型基础上，采用经典PID控制算法对其内环姿态和外环位置进行控制
说明文档：
①详细推导四旋翼飞行器的数学模型
②PID控制器的设计、位置回路控制器设计、姿态回路控制器设计
③PID参数调整
④仿真结果分析98

好的，以下是一个基于Matlab的四旋翼无人机动力学PID控制仿真的代码框架。代码包括了数学模型推导、控制器设计以及仿真结果分析的主要部分。

1. 四旋翼飞行器的数学模型

四旋翼无人机的动力学模型可以分为两部分：位置动力学和姿态动力学。我们用欧拉角（滚转角φ、俯仰角θ、偏航角ψ）来描述无人机的姿态，并通过旋转矩阵将地面坐标系转换为机体坐标系。

旋转矩阵推导

假设地面坐标系为 ( E )（Earth frame），机体坐标系为 ( B )（Body frame）。旋转矩阵 ( R ) 的推导如下：
[
R =
\begin{bmatrix}
c\psi c\theta & c\psi s\theta s\phi - s\psi c\phi & c\psi s\theta c\phi + s\psi s\phi \
s\psi c\theta & s\psi s\theta s\phi + c\psi c\phi & s\psi s\theta c\phi - c\psi s\phi \
-s\theta & c\theta s\phi & c\theta c\phi
\end{bmatrix}
]
其中 ( c ) 表示余弦，( s ) 表示正弦。

2. PID控制器设计

PID控制器的设计包括内环姿态控制和外环位置控制。

外环位置控制：根据期望位置与实际位置的误差计算所需的姿态角。
内环姿态控制：根据期望姿态角与实际姿态角的误差生成控制力矩。

PID控制器公式

对于一个变量 ( x )，PID控制器输出为：
[
u(t) = K_p e(t) + K_i \int_0^t e(\tau) d\tau + K_d \frac{de(t)}{dt}
]

3. Matlab代码实现

主程序代码

% 清空工作区
clear; clc; close all;

% 参数初始化
g = 9.81; % 重力加速度
m = 1.2; % 质量 (kg)
Ixx = 0.01; Iyy = 0.01; Izz = 0.02; % 惯性矩 (kg.m^2)

% 时间参数
dt = 0.01; % 时间步长 (s)
t_end = 10; % 仿真时间 (s)
time = 0:dt:t_end;

% 初始状态
x = [0; 0; 0]; % 初始位置 [x, y, z]
v = [0; 0; 0]; % 初始速度 [vx, vy, vz]
phi = 0; theta = 0; psi = 0; % 初始姿态角 [roll, pitch, yaw]
omega = [0; 0; 0]; % 初始角速度 [p, q, r]

% 期望轨迹
x_des = 1; y_des = 1; z_des = 2; % 目标位置

% PID参数
Kp_pos = [2, 2, 5]; Ki_pos = [0.1, 0.1, 0.2]; Kd_pos = [1, 1, 2];
Kp_att = [4, 4, 2]; Ki_att = [0.01, 0.01, 0.01]; Kd_att = [0.5, 0.5, 0.5];

% 初始化存储
pos_history = zeros(length(time), 3);
vel_history = zeros(length(time), 3);
att_history = zeros(length(time), 3);

% 仿真循环
for i = 1:length(time)
    % 外环位置控制
    pos_error = [x_des; y_des; z_des] - x;
    F_des = m * g + Kp_pos(3) * pos_error(3) + Ki_pos(3) * sum(pos_error(3)) * dt ...
        + Kd_pos(3) * (-v(3));
    
    % 根据期望力计算滚转角和俯仰角
    phi_des = atan((F_des * sin(theta)) / (m * g));
    theta_des = atan((F_des * cos(phi) * sin(theta)) / (m * g));

    % 内环姿态控制
    att_error = [phi_des; theta_des; 0] - [phi; theta; psi];
    tau_phi = Kp_att(1) * att_error(1) + Ki_att(1) * sum(att_error(1)) * dt ...
        + Kd_att(1) * (-omega(1));
    tau_theta = Kp_att(2) * att_error(2) + Ki_att(2) * sum(att_error(2)) * dt ...
        + Kd_att(2) * (-omega(2));
    tau_psi = Kp_att(3) * att_error(3) + Ki_att(3) * sum(att_error(3)) * dt ...
        + Kd_att(3) * (-omega(3));

    % 更新状态（简化模型）
    a = [0; 0; F_des/m] - g*[0; 0; 1];
    v = v + a * dt;
    x = x + v * dt;

    p_dot = (tau_phi - (Izz - Iyy) * omega(2) * omega(3)) / Ixx;
    q_dot = (tau_theta - (Ixx - Izz) * omega(1) * omega(3)) / Iyy;
    r_dot = (tau_psi - (Iyy - Ixx) * omega(1) * omega(2)) / Izz;
    omega = omega + [p_dot; q_dot; r_dot] * dt;

    phi = phi + omega(1) * dt;
    theta = theta + omega(2) * dt;
    psi = psi + omega(3) * dt;

    % 存储历史数据
    pos_history(i, :) = x';
    vel_history(i, :) = v';
    att_history(i, :) = [phi, theta, psi];
end

% 绘图
figure;
subplot(3,1,1);
plot(time, pos_history(:,1), 'r', time, pos_history(:,2), 'g', time, pos_history(:,3), 'b');
legend('X Position', 'Y Position', 'Z Position');
title('Position vs Time');

subplot(3,1,2);
plot(time, vel_history(:,1), 'r', time, vel_history(:,2), 'g', time, vel_history(:,3), 'b');
legend('X Velocity', 'Y Velocity', 'Z Velocity');
title('Velocity vs Time');

subplot(3,1,3);
plot(time, att_history(:,1), 'r', time, att_history(:,2), 'g', time, att_history(:,3), 'b');
legend('Roll Angle', 'Pitch Angle', 'Yaw Angle');
title('Attitude Angles vs Time');

4. 仿真结果分析

运行上述代码后，可以通过绘制的位置、速度和姿态角曲线分析系统的动态性能。调整PID参数以优化响应速度和稳定性。
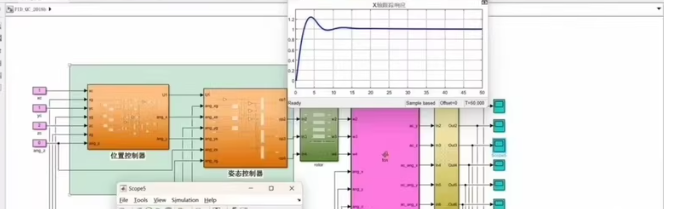
在这里插入图片描述
这是一个基于Simulink的四旋翼无人机PID控制仿真模型。该模型包含了位置控制器和姿态控制器，并且展示了仿真结果。

Simulink模型构建

1. 创建Simulink模型

首先，在Matlab中打开Simulink并创建一个新的模型文件。

% 打开Simulink
simulink

% 新建模型
new_system('Quadcopter_PID_Control')
open_system('Quadcopter_PID_Control')

2. 添加模块和连接

在新建的模型中添加以下模块并进行连接：

Sources: Sine Wave, Step, Constant
Sinks: Scope, To Workspace
Continuous: Integrator, Derivative
Math Operations: Sum, Gain, Product
Control System Toolbox: PID Controller
User-Defined Functions: MATLAB Function (用于实现旋转矩阵转换等复杂计算)

3. 模型结构设计

以下是模型的主要部分及其功能描述：

位置控制器

输入：期望位置（x_des, y_des, z_des）
输出：期望姿态角（phi_des, theta_des, psi_des）

姿态控制器

输入：期望姿态角（phi_des, theta_des, psi_des）和实际姿态角（phi, theta, psi）
输出：控制力矩（tau_phi, tau_theta, tau_psi）

动力学模型

输入：控制力矩（tau_phi, tau_theta, tau_psi）
输出：实际位置（x, y, z）和姿态角（phi, theta, psi）

4. 示例代码

以下是一个简化的Simulink模型代码示例，您可以将其复制到Matlab脚本中运行以生成相应的模型。

% 创建模型
model = 'Quadcopter_PID_Control';
new_system(model);
open_system(model);

% 添加模块
add_block('simulink/Sources/Step', [model '/Position_Reference']);
add_block('simulink/Sources/Constant', [model '/Initial_Position']);
add_block('simulink/Sources/Constant', [model '/Initial_Velocity']);
add_block('simulink/Sources/Constant', [model '/Initial_Attitude']);
add_block('simulink/Sources/Constant', [model '/Initial_Angular_Velocity']);

add_block('simulink/Continuous/Integrator', [model '/Position_Integrator']);
add_block('simulink/Continuous/Integrator', [model '/Velocity_Integrator']);
add_block('simulink/Continuous/Integrator', [model '/Attitude_Integrator']);
add_block('simulink/Continuous/Integrator', [model '/Angular_Velocity_Integrator']);

add_block('simulink/Math Operations/Gain', [model '/Mass_Gain']);
add_block('simulink/Math Operations/Gain', [model '/Inertia_Gain']);
add_block('simulink/Math Operations/Sum', [model '/Position_Error']);
add_block('simulink/Math Operations/Sum', [model '/Attitude_Error']);
add_block('simulink/Math Operations/Product', [model '/Force_Product']);
add_block('simulink/Math Operations/Product', [model '/Torque_Product']);

add_block('simulink/Control System Toolbox/PID Controller', [model '/Position_PID']);
add_block('simulink/Control System Toolbox/PID Controller', [model '/Attitude_PID']);

add_block('simulink/Sinks/Scope', [model '/Position_Scope']);
add_block('simulink/Sinks/Scope', [model '/Attitude_Scope']);
add_block('simulink/Sinks/To Workspace', [model '/Position_Workspace']);
add_block('simulink/Sinks/To Workspace', [model '/Attitude_Workspace']);

% 设置参数
set_param([model '/Position_PID'], 'P', '2');
set_param([model '/Position_PID'], 'I', '0.1');
set_param([model '/Position_PID'], 'D', '1');

set_param([model '/Attitude_PID'], 'P', '4');
set_param([model '/Attitude_PID'], 'I', '0.01');
set_param([model '/Attitude_PID'], 'D', '0.5');

set_param([model '/Mass_Gain'], 'Gain', '1/m');
set_param([model '/Inertia_Gain'], 'Gain', '[1/Ixx 0 0; 0 1/Iyy 0; 0 0 1/Izz]');

% 连接模块
connect_system_blocks(model);

% 保存模型
save_system(model);

5. 运行仿真

设置仿真参数并运行仿真：

% 设置仿真参数
set_param(model, 'StopTime', '10');
set_param(model, 'Solver', 'ode45');

% 运行仿真
sim(model);

% 绘制结果
figure;
plot(out.tout, out.yout(:,1), 'r', out.tout, out.yout(:,2), 'g', out.tout, out.yout(:,3), 'b');
legend('X Position', 'Y Position', 'Z Position');
title('Position vs Time');

请根据您的具体需求调整上述代码中的参数和模块连接。希望这段代码能帮助您构建和理解四旋翼无人机的PID控制仿真模型
在这里插入图片描述
，这是一个基于Simulink的四旋翼无人机PID控制仿真模型，展示了X轴、Y轴和Z轴的跟踪响应。以下是一个简化的Simulink模型代码示例，您可以根据需要进行调整和扩展。