一、卡尔曼滤波:
卡尔曼滤波(也称为线性二次估计)是一种算法,它使用随时间观察的一系列测量值(包括统计噪声和其他不准确性)和已知的控制输入变量来生成未知变量的最优估计值。
实例解释:如何准确知道一辆行驶中的汽车的位置?
方案1(状态方程):汽车需要遵循物理定律,可以通过对其速度随时间进行积分来估计其位置,该速度(控制输入变量)可通过跟踪车轮转速和方向盘的角度来确定的。但汽车过程中存在各种阻力影响,以及各种突发状况,难以准确计算实际位置。
方案2(观测方程):GPS定位,但GPS 精度不足,信号传递容易受到干扰,估计的位置只能保持在距离真实位置几米的范围内,不够精确。
为了准确获得小车位置引入卡尔曼滤波算法。
1、(线性)卡尔曼滤波应用的假设前提:
- 当前时刻状态只和上一时刻状态有关。
- 模型和系统均满足线性关系。
- 引入的噪声符合高斯分布(正态分布)。
2、公式:

xk 表示k时刻的真实值,是待估计的值
xk-1 表示k1时刻的真实值 (用上一个状态的最优估计值代表真实值)
uk-1 表示k1时刻的控制输入量
zk k时刻的观测值
随机变量wk ,vk 分别表示过程噪声和观测噪声,通常假设他们彼此独立且符合正态分布的白噪声(均值等于0)
p( wk ) ~N (0,Qk) Qk为状态噪声协方差矩阵
p( vk) ~N (0,Rk ) Rk为量测噪声协方差矩阵,
F 、B、H分别表示状态转移矩阵、控制矩阵、观测转移矩阵。
3、推到过程:
1)示例解释状态空间方程




二、扩展卡尔曼滤波(EKF)算法
扩展卡尔曼滤波(Extended Kalman Filter,EKF)通过局部线性来解决非线性的问题。将非线性的状态方程和观测方程进行求导,以切线代替的方式来线性化,即,在均值处进行一阶泰勒展开。
1、非线性系统状态方程与观测方程为:

Xk 当前时刻的状态值;
Yk 当前时刻的测量值;
Uk 表示控制向量;
Гk 表示状态噪音系数矩阵;
Wk 为状态噪声, p( wk ) ~N (0,Qk) Qk为状态噪声协方差矩阵;
Vk 为量测噪声, p( vk) ~N (0,Rk ) Rk为量测噪声协方差矩阵;
Wk , Vk 不相关。

2、EKE算法及计算步骤:

计算步骤:
1、初始条件:确定状态初始值 以及误差协方差初始值Po/o
2、求先验估计
3、求先验估计误差的协方差矩阵
4、求卡尔曼增益
5、求后验估计,得到最优估计值
6、求后验估计误差的协方差矩阵,用于下一轮计算
7、重复1~6 步骤循环计算
三、基于EKF算法的SOC估算方法
1、一阶RC网络等效电路模型(Thevenin模型)

电压源:UOC描述动力电池的开路电压;
欧姆内阻:R0表示动力电池电极材料、电解液、隔膜电阻及各部分零件的接触电阻。
RC网络:R1和C1分别为极化内阻和极化电容;
U为R1并联环节的电压降,用于模拟动力电池的极化电压。
端电压Ut:模型对外输出电压,可以直接采集到的电压值
1)建立状态方程与观测方程:
电路模型方程为:
2)根据状态方程和观测方程,得到EKE算法需要的矩阵:

3)根据上述EKE算法构建公式,并进行计算。
2、二阶RC网络等效电路模型(PNGV模型)

该模型使用两个RC并联环节描述动力电池极化特性,其电路模型的方程









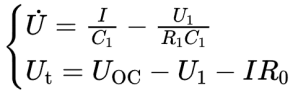

















 939
939

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








