《算法面试“必杀技”：双指针法高效解决数组原地操作》

原创于 2025-10-04 15:21:36 发布 · 591 阅读

20 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构 #开发语言 #面试 #其他 #c语言 #c++

《数据结构与算法刷题集》专栏收录该内容

1 篇文章

订阅专栏

🔥@晨非辰Tong：个人主页

👀专栏：《C语言》、《数据结构与算法》

💪学习阶段：C语言、数据结构与算法初学者

⏳“人理解迭代，神理解递归。”

引言：告别盲目刷题。学完顺序表后，集中攻克「删除有序数组重复项」、「移除元素」、「合并有序数组」这三道题，你将能一举掌握解决一大类数组问题的双指针技巧。

1. 力扣_26. 删除有序数组中的重复项（双“指针”法）

2. 力扣_27. 移除元素（双“指针”法）

3. 88. 合并两个有序数组 - 力扣（LeetCode）

1. 26. 删除有序数组中的重复项- 力扣（LeetCode）（双“指针”法）

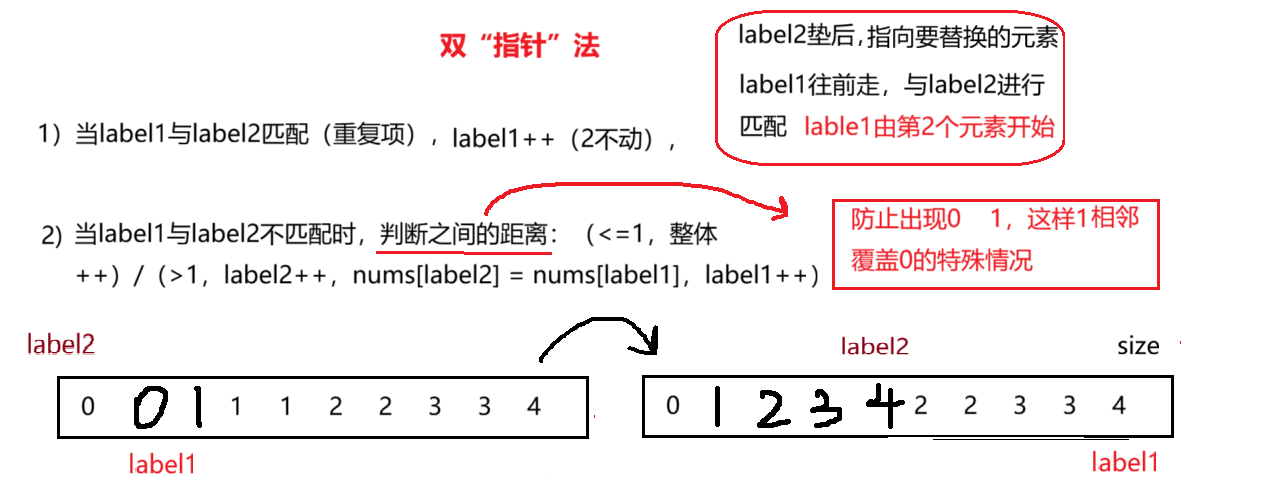
--本题采用的方法为经典的双“指针”法（不是真的两个指针，只是两个变量的指向作用充当“指针”），此方法在以后的学习中经常会使用到。

--在结合前面所学的时间复杂度、空间复杂度舍弃了另外一种普遍、容易想到办法——>创建临时数组，将符合的元素拷贝到临时数组中，再进行数组值间的拷贝。

int removeDuplicates(int* nums, int numsSize) 
{
    //定义两个“指针”
    int label1 = 1, label2 = 0;
    while(label1 < numsSize)
    {
        //匹配
        if(nums[label2] == nums[label1])
        {
            label1++;
        }
        
        //不匹配
        else
        {
            //判断label之间的距离
            // <= 1
            if((label1 - label2) <= 1)
            {
                label1++;
                label2++;
            }
            //>1
            else
            {
                label2++;
                nums[label2] = nums[label1];
                label1++;
            }
        }
    }

    return label2 + 1;
}

--本题的解题参照为示例2（相较于示例1，涉及到的情况更加复杂，易考虑全面）。

使用两个标记点来遍历数组，第一个标记点指向当前不重复数字的最后一个位置，第二个标记点负责在前面寻找新的不重复数字。

初始化两个标记点：label2从0开始，label1从1开始。让label1逐个检查数组中的每个数字，当label1发现与label2不同的数字时：

如果两个标记点相邻，就一起向前移动

如果两个标记点不相邻，先把label2向前移动一位，再把label1的数字复制过来

重复这个过程直到label1遍历完整个数组

最终返回label2+1作为新数组的长度

2. 27. 移除元素- 力扣（LeetCode）（双“指针”法）

--方法：双“指针”法

--本道题的解法仍旧使用双“指针”法。

--在结合前面所学的时间复杂度、空间复杂度舍弃了另外一种普遍、容易想到办法——>创建临时数组，将符合的元素拷贝到临时数组中，再进行数组值间的拷贝。

int removeElement(int* nums, int numsSize, int val) 
{
    int src = 0, dst = 0;
    while(src < numsSize)
    {
            src是val，src++
        if(nums[src] == val)
        {
            src++;
        }

            src非val，赋值，整体++
        else
        {
            nums[dst] = nums[src];
            dst++;
            src++;
        }
       
    }
    return dst;
}

//优化
int removeElement(int* nums, int numsSize, int val) 
{
    int src = 0, dst = 0;
    while(src < numsSize)
    {
        if(nums[src] != val)
        {
            nums[dst] = nums[src];
            dst++;
        }
        src++;
       
    }
    return dst;
}

示例一：要求k=2，两个非val值

--开头 src、dst 都在数组第一个元素，恰好 src = val（3），那么 src++（dst 不动，指向val值）。src = 2（非val），那么 nums[dst] = nums[src](2覆盖3)，整体++。src = 2（非 val，dst指向空），src再++（dst不动）……最后src超过numsSize(循环终止条件)，dst 指向nums[2]——>dst=2（要求返回的k值）。

3. 88. 合并两个有序数组 - 力扣（LeetCode）

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) 
{
    int l1 = m - 1;
    int l2 = n - 1;
    int l3 = m + n -1;
    while(l1 >= 0 && l2 >= 0)
    {
        //比较l1、l2谁数值大
        if(nums1[l1] > nums2[l2])
        {
            nums1[l3--] = nums1[l1--];
        }
        else
        {
            nums1[l3--] = nums2[l2--];
        }
    }
    //l1访问越界（l2没有越界，进行特殊的处理）
    while(l2 >= 0)
    {
        nums1[l3--] = nums2[l2--];
    }
    //l2越界（不处理）
    //l1、l2同时越界（不存在）
}

回顾：