学会这个你也是一个数据分析师！！！

学会这个你也是一个数据分析师！！！

一元线性回归模型

今天请的同学是某985硕士在读的C同学的讲解，希望能够帮助在学习机器学习和统计知识的同学们，帮助广大统计生和专攻知识的同学们更上一层楼。

• 实际背景

在现实生活和众多研究领域中，常常需要探究两个变量之间的关系。例如在经济学里，商品的价格与销售量之间可能存在某种关联；在物理学中，物体所受的力与产生的加速度之间也存在关系。当我们发现两个变量之间似乎呈现出一种线性的趋势，即一个变量的变化会引起另一个变量近似成比例地变化时，就可以考虑使用一元线性回归模型来对这种关系进行定量分析和预测。通过建立两者的线性关系模型，能够帮助我们根据已知变量的值来预测未知变量的值，从而为决策、研究等提供依据。市面上的Deepseek，Claude3.5等大模型，也会分出一部分用于一元线性回归，主要是避免一定程度模型复杂计算复杂过拟合等情况。

可以看出一元线性回归，在统计测量领域具有一定的权威性和启蒙性。

• 数学形式
• 
• 

公式

• 参数估计

通常使用最小二乘法来估计模型中的参数。其基本思想是找到一组参数值，使得样本数据点到回归直线（在一元线性回归中，模型对应的是一条直线）的误差平方和最小。

误差平方和公式:

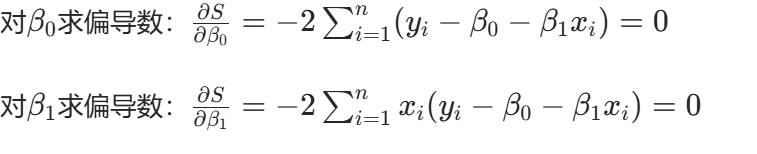
通过求解上述方程组，我们可以得到参数的估计值：

• 回归方程的显著性检验

回归方程的显著性检验是为了判断所建立的一元线性回归方程是否具有实际意义，也就是检验自变量x和因变量y之间是否确实存在线性关系。以下是几种常用的检验方法：

F检验

t检验

决定系数

• 小结

一元线性回归模型作为一种基础且关键的数据分析工具，通过确立自变量和因变量之间的线性关系，实现了对未知数据的预测功能。在实际应用过程中：

1.首先要从具体的实际背景出发，精准确定合适的自变量和因变量，并全面收集相关数据。数据的质量和相关性直接影响模型的准确性和有效性 。

2. 接着运用最小二乘法来估计模型参数，进而得到具体的回归方程。这一步骤是模型构建的核心环节，参数估计的准确性决定了回归方程的可靠性 。

3. 然后对回归方程进行显著性检验，通过多种检验方法如F检验、t检验、决定系数R^2来判断模型是否有效，以及自变量和因变量之间的线性关系是否显著。只有通过检验的模型才具有实际应用价值 。

尽管一元线性回归模型原理相对简洁明了，但它是理解更为复杂的回归模型（如多元线性回归、非线性回归等）的重要基石。同时，在众多实际场景中，它也能发挥重要的作用，例如在市场调研、质量控制、经济预测等领域都有广泛应用。然而，该模型也存在一定的局限性，例如它要求变量之间必须是严格的线性关系，对异常值较为敏感等。因此，在实际应用时，需要根据具体情况合理选择和运用该模型，必要时还需结合其他方法对模型进行改进和优化。

最后小编想到了一句诗：

十年寒窗无人问，一举成名天下知。

望各位成功抵达梦想的彼岸。

下一站：多元线性回归，我们再见！！！！