数据结构-练习6 线索二叉树的建立和遍历

   前面一篇博客讲述了二叉树的建立和遍历，无论是前序还是中序或是后序，只不过是访问数据的顺序不一样，是为了访问二叉树而人为化的一种链式“形”，突出的是访问的内在联系。同样地，线索化的二叉树也是，在前驱和后继之间建立起一种联系，从而使访问特别快，特别方便。

 

    线索化二叉树是在二叉树的序（前，中，后）的基础上建立起来的。其关键是利用空闲的lchild和rchild存储其前驱和后继，对于度为2 的节点，lchild和rchild！=null,已经存储了相关信息。所以线索化二叉树时，就是找出lchild和rchild(==null)的节点，然后使lchild和rchild分别指向前驱和后继。为了遍历线索化二叉树时，我们能有效区分lchild(rchild)是存储了左子树（右子树）还是存储了前驱（后继），我们可以增加两个有效标志位lfag,rflag。具体原理见如下：

                                                                                                                  

                                                                                                                                  

                                                                                  

 

 

 

 

 

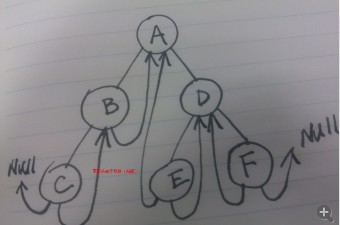
   仿造普通的”线索“的表示，箭头线段分别表示，前驱和后继，注意：箭头线段的节点没有左子树（右子树）。

    采用的节点数据结构：

                                           

typedef struct Tnode
{
 char data;
 Tnode* lchild;
 Tnode* rchild;
 bool lflag;
 bool rflag;

}

我采用前序创建二叉树，前序遍历，中序线索化二叉树，然后线索遍历二叉树，共四个函数。

 

代码如下：

 

        

#include<iostream>
using namespace std;
typedef struct Tnode
{
 char data;
 Tnode* lchild;
 Tnode* rchild;
 bool lflag;
 bool rflag;

} BiTnode,* BiTree;

//前序建立二叉树
void CreateBiTree(BiTree* T)
{
 char inputChar;
 cin>>inputChar;
 //空子树
 if(inputChar=='#')
  {
  *T=0;
  return ; 
 
  }
 else
	
 {   
 (*T)=(BiTree)malloc(sizeof(BiTnode));
 if(!(*T)) throw "Invalid Address";
 else
 {
 (*T)->data=inputChar;
 (*T)->lflag=0;
 (*T)->rflag=0;
 CreateBiTree(&((*T)->lchild));
 CreateBiTree(&((*T)->rchild));
 }
 }

}

//前序遍历二叉树
void preTraverse(BiTree T)
{
	
 if(T)
 {
	 cout<<T->data<<",";
	 preTraverse(T->lchild);
	 preTraverse(T->rchild);
 }


}

//中序二叉树线索化
void inThreadedBiTree(BiTree T,BiTree * h )
{
  if(T!=NULL)
  {
	  inThreadedBiTree(T->lchild,h);
	  if(T->lchild==NULL)
	  {
		  T->lchild=*h;
		  T->lflag=1;
	  
	  }
	  if(*h!=NULL&&((*h)->rchild==NULL))
	  {
		  (*h)->rchild=T;
		  (*h)->rflag=1;
	  
	  }
	  *h=T;//采用二级指针的意义就在于此，为了指向T,T一级指针，这样可以省空间
	  inThreadedBiTree(T->rchild,h);
  
  }


}
//线索遍历二叉树
void inThreadTraverse(BiTree T)
{
  BiTree h;
  if(T==NULL)return;
  h=T;
  while(h->lflag==0)h=h->lchild;
  cout<<h->data<<",";
  while(h->rchild!=NULL)
  {
	  if(h->rflag==1)
		  h=h->rchild;
	  else
	  {
		  h=h->rchild;
		  while((h->lflag==0)&&(h->lchild!=NULL))
			  h=h->lchild;
	  }
	  cout<<h->data<<",";
  }

}

int main()
{
	BiTree* T=(BiTree*)malloc(sizeof(BiTree*));;
    CreateBiTree(T);
	cout<<"前序输出二叉树："<<endl;
    preTraverse(*T);
	BiTree h=NULL;
    inThreadedBiTree( *T, &h );
    cout<<endl<<"线索遍历：";
	inThreadTraverse(*T);
    
    return 0;
 }

注：其他方法（前序线索和后序线索）类似，明白原理即可，要用再查书。可见线索化二叉树，只是引入了一种遍历的方式而已，其带来的劣势是：增加了空间。

 

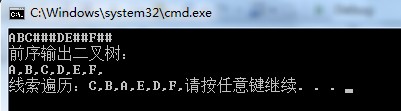
测试结果：按开始给出的示意图：输入 ABC###DE##F##

 

                                                                                                 

 

          分两种情况，rchild!=null，即不存在右子树的，按后继链寻找，反之，按原遍历顺序寻找，直到末尾点，读者可按运行结果笔画一下。