分位数的含义:
以10%分位数为例,10%分位数是指将一组数据按照从小到大的顺序排列后,处于第10%位置的数值。换句话说,它是将数据集分成10等份时,位于第一份的最大值。
计算10%分位数的方法如下:
-
将数据集按照从小到大的顺序进行排序。
-
计算出数据集的总个数(n)。
-
计算出位置索引(index):index = (10/100) * (n + 1)。
-
如果index是整数,则10%分位数为排序后的第index个数值。
-
如果index不是整数,则10%分位数可以通过线性插值来计算。假设index的整数部分为k,小数部分为d,那么10%分位数可以近似表示为:10%分位数 = (1-d) * 第k个数值 + d * 第(k+1)个数值。
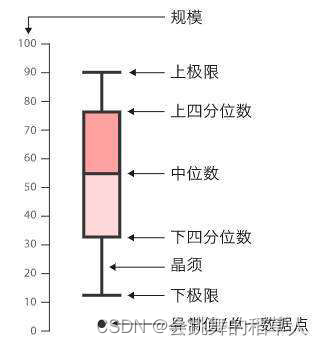
boxplot(箱线图,又称为盒须图、盒式图)是在1977年由美国统计学家John Tukey发明,分析数据需要为定量数据。通过箱线图,可以直观的探索数据特征。
箱线图共由五个数值点构成,分别是最小观察值,25%分位数(Q1),中位数,75%分位数(Q3),最大观察值。需要特别说明的是,最小观察值和最大观察值定义如下:
-
最小观察值 = Q1 – 1.5(IQR), IQR = Q3 –Q1
-
最大观察值 = Q3 + 1.5(IQR), IQR = Q3 –Q1
-
箱线图中,‘下限’为最小观察值与真实最小值之间的较大值;‘上限’为最大观察值与最大值之间的较小值。
-
如果数据有存在离群点即异常值,他们大于超出最大或者最小观察值,此时此将离群点以“圆点”形式进行展示。
下图显示了箱型图与正态分布的概率分布函数的比较。盒子本身就是四分位数范围,它包含了50%的数据。此外,请注意每个箱须包含分布的24.65%,而不是精确的25%。箱形图认为超出箱须的观察值是离群值。

何时用箱线图:
个人认为,某一定量数据包含一类含有多个特征的定类数据如一个班的各科(定类)成绩(定量)。 通过各科成绩的箱型图分布来对比不同科目之间的差异(数据总体分布,上下限,波动程度,平均值,异常值)。
如何观察:
箱型图可以让我们快速评估分布的集中趋势、方差和偏度。
集中趋势
在下图中,A组的中位线比B组高。事实上,很容易看出A组的整个分布相对于B组来说是向上移动的。(其实就是通过箱体高度,晶须长短,以及二者的位置分布来整体比较,把握数据分布状态)

偏度
要确定一个分布在箱形图中是否呈偏态,要看中位数线在箱体和箱须中的位置。当箱体的中心大约在中位线上,并且上、下须大约等长时,我们就有一个对称的分布(正态分布)。对于标准正态分布的大样本,只有 0.7%的值是异常值,中位数位于上下四分位数的中央,箱形图的方盒关于中位线对称。
如果两边不大致相等,我们的分布就是呈偏态的。当中位数更接近箱体的下限值,且上须更长时,它就是一个右偏分布。请注意,在下面的方框和箱须图中,长须是如何延伸到较高的数值中的,使其成为正偏态。

当中位数更接近箱体的高值时,它是一个左偏的分布,而下边的箱须更长。请注意,长须向低值延伸,使其呈负偏态。

总结一下:将箱型图逆时针旋转90°,此时中位数靠左(数轴负数方向)就是左偏,呈负偏态;中位数靠右(数轴正数方向)就是右偏,呈正偏态。
群组比较
来自R语言里面的boxplot的example。这个箱线图共涉及3个变量。定量变量是牙齿生长长度,体现在图形的纵坐标,也就是箱子展示的内容。第一个定性变量是维他命C的剂量,三个水平(0.5mg,1mg和2mg),体现在横坐标,所以一共有3组箱线图;第二个定性变量是食用的食物,是维C还是橙汁,分别用黄色和橙色展现,所以每组箱线图里又包含两个箱子。

从图中可以看出
- 随着使用剂量的增加,不管食用的是哪种食物,牙齿生长长度的平均水平(中位数)都在增加。
- 当使用剂量为0.5mg和1mg时,食用橙汁带来的牙齿生长的平均长度(中位数)要比食用维C高,波动程度也相应更大。
- 当使用剂量为2mg时,食用两种食物带来的牙齿生长平均水平(中位数)相当,食用维C的牙齿生长长度波动相对更大。

从图中可以看出
- 课程成绩的分布状态正态、左偏、右偏等(中位数相对于箱体的高低)
- 成绩集中程度(箱体越短,成绩越集中)
- 各组数据平均成绩的高低(中位数相对于其他数据的高低)
- 数据的波动程度(箱体和晶须整体越长,数据波动越大)
案例
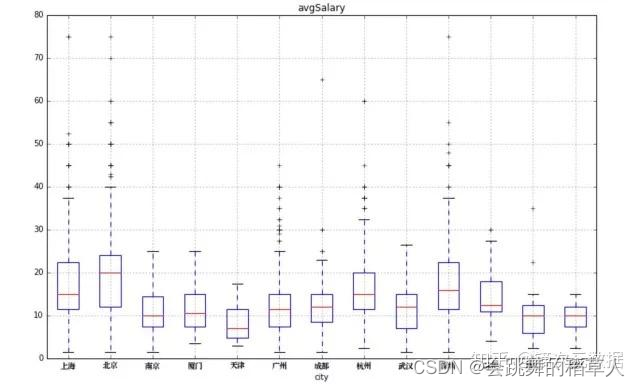
从图中可以看出
- 中的红线显然是各个城市中游水平的数据分析师能够获得的薪资标准,上边的蓝线区间为中上游,下边的蓝线区间为中下游,以此类推。简而言之,样本人群被四等分了。
- 上海、北京、深圳的数据分析师,薪资范围接近,但是中上游水平的人,北京地区能获得更高的薪资(中位数(Q2)的位置更高)。
- 西安、长沙、天津则不利于数据分析师的发展(总体薪资低,上下限也低)。
- 杭州的水平接近北上深,但是薪资上限受到一定限制。
主要参考:























 941
941

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








