首先来说一下什么是最小生成树:
由 V 中的全部 n 个顶点和 E 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。
我们通常有两种方法求最小生成树,一种是prim算法,另一种就是kruskal算法,下面我将对这两种算法进行介绍,首先我要说明的是这两种算法都是利用的贪心思想:
prim(不断地加点)
我们首先选取一个点,然后利用这个点来更新所有与这个点有边的点的距离,然后选取距离最小的那个点加入,不断地重复这个过程,直至把所有点都加入。
我下面给出的代码是dijkstra算法堆优化改变版的,复杂度是nlogn,算法实现上基本与dijksta算法一致,但是需要注意的是,我们考虑最小生成树时一定要先看看图是否连通,所以要对dist数组中的每一个值查询一遍,若出现不连通现象,那图中将不会存在最小生成树。
核心代码:
long long prim()
{
priority_queue<PII,vector<PII>,greater<PII> >q;//用一个优先队列来存储被更新的点及其现在边的长度
memset(dist,0x3f,sizeof dist);//更新距离数组
q.push({0,1});
dist[1]=0;
long long ans=0;
while(q.size())
{
int dis=q.top().first,begin=q.top().second;
q.pop();//千万不能忘记出队列,否则会陷入死循环
if(vis[begin]) continue;//如果这个点已经被更新过,就不用再次更新,否则可能会出现TLE
vis[begin]=true;//标记为已遍历
ans+=dis;//加入最小生成树的边
for(int i=h[begin];i!=-1;i=ne[i])//链式向前星存图
{
int j=e[i];
if(dist[j]>w[i])//更新的是未在连通图的点的最小距离
{
dist[j]=w[i];
q.push({dist[j],j});//将被更新的点加入队列
}
}
}
return ans;//返回最小生成树长度
} for(int i=1;i<=n;i++)//判断图是否连通
if(dist[i]==0x3f3f3f3f)
{
puts("impossible");
return 0;
}下面我来介绍一下kruskal算法(加边法)
实现方法:
首先对所有边进行大小排序,我们尽可能每次加入权值小的边,在加边过程中不能出现环,根据树的性质我们容易知道,n个点的图最小生成树具有n-1条边,我们如果加到最后是n-1条边的话,那么我们求出来的就是最小生成树的大小。
那我们怎样判断加边的过程中会不会出现环呢?根据最小连通图的性质我们知道,如果在两个不连通的图之间加一条边,必然不会产生环,若边加在连通图内部,则一定会产生环,提到这想必大家都应该知道这个算法应该怎么实现了吧,对,就是并查集,判断加边后会不会成环就转变为判断这个边的两个集合在加边前在不在一个集合中,剩下的就不用多说了吧,直接上代码!
核心代码:
bool cmp(node a,node b)//结构体排序(权值为排序关键词)
{
return a.w<b.w;
}
int find(int x)//并查集
{
if(x!=fu[x]) fu[x]=find(fu[x]);
return fu[x];
}for(int i=1;i<=m;i++)
{
int f1=find(p[i].a),f2=find(p[i].b);//找出待加边两端点的所在集合
if(f1!=f2)//说明加边后不会成环
{
fu[f1]=f2;
ans+=p[i].w;
cnt++;
}
}
if(cnt<n-1) puts("impossible");//说明图不是连通的 下面给出一道题并给出两种做法
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 G=(V,E),其中 V 表示图中点的集合,E 表示图中边的集合,n=|V|,m=|E|。
由 V 中的全部 n 个顶点和 E 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含三个整数 u,v,w,表示点 u 和点 v 之间存在一条权值为 w 的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
数据范围
1≤n≤500
1≤m≤10^5
图中涉及边的边权的绝对值均不超过 10000。
输入样例:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例:
6prim算法代码
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
typedef pair<int,int> PII;
const int N=300003;
int h[N],dist[N],e[N],w[N],ne[N],idx;
bool vis[N];
int n,m;
void add(int x,int y,int z)
{
e[idx]=y;
w[idx]=z;
ne[idx]=h[x];
h[x]=idx++;
}
long long prim()
{
priority_queue<PII,vector<PII>,greater<PII> >q;//用一个优先队列来存储被更新的点及其现在边的长度
memset(dist,0x3f,sizeof dist);//更新距离数组
q.push({0,1});
dist[1]=0;
long long ans=0;
while(q.size())
{
int dis=q.top().first,begin=q.top().second;
q.pop();//千万不能忘记出队列,否则会陷入死循环
if(vis[begin]) continue;//如果这个点已经被更新过,就不用再次更新,否则可能会出现TLE
vis[begin]=true;//标记为已遍历
ans+=dis;//加入最小生成树的边
for(int i=h[begin];i!=-1;i=ne[i])//链式向前星存图
{
int j=e[i];
if(dist[j]>w[i])//更新的是未在连通图的点的最小距离
{
dist[j]=w[i];
q.push({dist[j],j});//将被更新的点加入队列
}
}
}
return ans;//返回最小生成树长度
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof h);
for(int i=1;i<=m;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
add(y,x,z);
}
long long ans=prim();
for(int i=1;i<=n;i++)//判断图是否连通
if(dist[i]==0x3f3f3f3f)
{
puts("impossible");
return 0;
}
cout<<ans;
return 0;
}kruskal算法代码
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=300003;
int fu[N];
struct node{
int a,b,w;//a,b,c分别是边的始点和终点以及权值
}p[N];
bool cmp(node a,node b)//结构体排序(权值为排序关键词)
{
return a.w<b.w;
}
int find(int x)//并查集
{
if(x!=fu[x]) fu[x]=find(fu[x]);
return fu[x];
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) fu[i]=i;
for(int i=1;i<=m;i++)
{
int u,v,w;
cin>>u>>v>>w;
p[i]={u,v,w};
}
sort(p+1,p+m+1,cmp);
long long ans=0,cnt;
for(int i=1;i<=m;i++)
{
int f1=find(p[i].a),f2=find(p[i].b);//找出待加边两端点的所在集合
if(f1!=f2)//说明加边后不会成环
{
fu[f1]=f2;
ans+=p[i].w;
cnt++;
}
}
if(cnt<n-1) puts("impossible");//说明图不是连通的
else printf("%lld",ans);
return 0;
}下面我再给出一道例题并给出kruskal算法的相应代码
某省调查乡村交通状况,得到的统计表中列出了任意两村庄间的距离。省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通(但不一定有直接的公路相连,只要能间接通过公路可达即可),并要求铺设的公路总长度为最小。请计算最小的公路总长度。
Input
测试输入包含若干测试用例。每个测试用例的第1行给出村庄数目N ( < 100 );随后的N(N-1)/2行对应村庄间的距离,每行给出一对正整数,分别是两个村庄的编号,以及此两村庄间的距离。为简单起见,村庄从1到N编号。
当N为0时,输入结束,该用例不被处理。
Output
对每个测试用例,在1行里输出最小的公路总长度。
Sample Input
3
1 2 1
1 3 2
2 3 4
4
1 2 1
1 3 4
1 4 1
2 3 3
2 4 2
3 4 5
0Sample Output
3
5#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int N=100003;
typedef long long ll;
struct node{
int a,b;
int w;
}p[N];
int fu[N];
int find(int x)
{
if(x!=fu[x]) fu[x]=find(fu[x]);
return fu[x];
}
bool cmp(node a,node b)
{
return a.w<b.w;
}
int main()
{
int n;
while(1)
{
scanf("%d",&n);
if(n==0) break;
for(int i=1;i<=n;i++) fu[i]=i;
int cnt=0,dis,x,y;
for(int i=1;i<n;i++)
for(int j=i+1;j<=n;j++)
{
scanf("%d%d%d",&x,&y,&dis);
p[++cnt]={i,j,dis};
}
sort(p+1,p+cnt+1,cmp);
ll ans=0;
for(int i=1;i<=cnt;i++)
{
int f1=find(p[i].a),f2=find(p[i].b);
if(f1!=f2)
{
ans+=p[i].w;
fu[f1]=f2;
}
}
printf("%lld\n",ans);
}
return 0;
}我再对这两种算法做一下简单对比吧!
prim算法在空间发杂度上可能更占优势,但显然kruskal算法的时间复杂度更为明显,况且我感觉kruskal算法实现起来比较容易,但如果出现待存储边较多的情况下,也就是说要存的图是一个稠密图,那我们最好还是用prim算法,尽量两种算法大家都能掌握。
下面我给出一道最小生成树的经典题目,我感觉解题思想还是挺好的
已知一个平面上有 n 个城市,需要个 n 个城市均通上电
一个城市有电,必须在这个城市有发电站或者和一个有电的城市用电缆相连
在一个城市建造发电站的代价是 c[i]
i 和 j 两个城市相连的代价是 k[i]+k[j] 乘上两者的曼哈顿距离
求最小代价的方案
输入:
第一行为城市个数
下面是每个城市的坐标
下面是建造发电站的代价 c[i]
下面是每个城市连线的系数 k[i]
输出:
一个为最小代价
建造发电站的城市数,然后分别输出建造发电站的城市
接着输出连线的条数,最后输出所连线的起始点。
任意一种即可,输出顺序任意
输入输出样例
输入 #1复制
3 2 3 1 1 3 2 3 2 3 3 2 3
输出 #1复制
8 3 1 2 3 0
输入 #2复制
3 2 1 1 2 3 3 23 2 23 3 2 3
输出 #2复制
27 1 2 2 1 2 2 3
说明/提示
For the answers given in the samples, refer to the following diagrams (cities with power stations are colored green, other cities are colored blue, and wires are colored red):
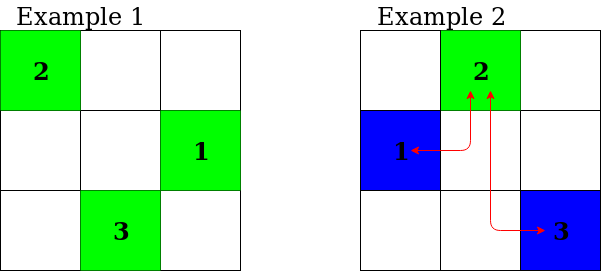
For the first example, the cost of building power stations in all cities is 3 + 2 + 3 = 83+2+3=8 . It can be shown that no configuration costs less than 8 yen.
For the second example, the cost of building a power station in City 2 is 2. The cost of connecting City 1 and City 2 is 2 \cdot (3 + 2) = 102⋅(3+2)=10 . The cost of connecting City 2 and City 3 is 3 \cdot (2 + 3) = 153⋅(2+3)=15 . Thus the total cost is 2 + 10 + 15 = 272+10+15=27 . It can be shown that no configuration costs less than 27 yen.
对这道题分析不难发现,如果去除发电站,那么这道题就是一道普通的最小生成树问题,所以关键就是如何处理这个发电站的问题,这里提供一个比较巧妙的方法,我们可以虚拟一个0号城市,如果建立发电站就等价于与0号城市连一条边,代价就是建立发电站的代价,再分别把各个城市之间连线的代价预处理出来,这样问题就转化为一个裸的最小生成树问题,再把与0号城市有连线的城市记录下来,即可得到建立发电站的城市,大致思路就是这样了,最后上代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<vector>
using namespace std;
const int N=2e6+10;
typedef long long ll;
ll fu[N],c[N],k[N];
ll cnt1[N];//记录每个城市连线的条数
ll vis[N];//记录发电站位置
typedef pair<long long,long long> PII;
struct city{
ll x,y;
}p[N];
struct node{
ll u,v,w;
}q[N];
bool cmp(node a,node b)
{
return a.w<b.w;
}
ll find(ll x)//并查集
{
if(x!=fu[x]) fu[x]=find(fu[x]);
return fu[x];
}
vector<PII> v;//记录连线起始点
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++) fu[i]=i;
for(int i=1;i<=n;i++)
scanf("%lld%lld",&p[i].x,&p[i].y);
for(int i=1;i<=n;i++) scanf("%lld",&c[i]);
for(int i=1;i<=n;i++) scanf("%lld",&k[i]);
int cnt=0;
for(int i=1;i<=n;i++)
for(int j=0;j<i;j++)//加一个0点,与0连线相当于建立发电站
{
if(j==0) q[++cnt]={j,i,c[i]};
else
q[++cnt]={j,i,(k[i]+k[j])*(abs(p[i].x-p[j].x)+abs(p[i].y-p[j].y))};
}
sort(q+1,q+cnt+1,cmp);
unsigned long long ans=0;
int count=0;
for(int i=1;i<=cnt;i++)
{
int f1=find(q[i].u),f2=find(q[i].v);
if(f1==f2) continue;
fu[f1]=f2;
ans+=q[i].w;
if(!q[i].u) count++,vis[q[i].v]=true;//标记发电站位置
else
{
v.push_back({q[i].u,q[i].v});
cnt1[q[i].u]++;cnt1[q[i].v]++;
}
}
printf("%lld\n%lld\n",ans,count);
for(int i=1;i<=n;i++)
if(vis[i])
printf("%d ",i);
printf("\n%lld\n",n-count);
for(int i=0;i<v.size();i++) printf("%lld %lld\n",v[i].first,v[i].second);
return 0;
}如果大家有什么更好的想法,欢迎在评论区里讨论!






















 878
878











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








