我在复习数据结构——时间复杂度计算时,发现很多地方都会用到求和式及其运算规则,故写下本文用以记录。
描述不准确、过程不严谨之处,还请理解。
一、求和式的基本概念
高中时我们学过数列,以及数列求和
根据数列前n项和的定义: 
而等式右边的多项式可以简写为求和式: 

求和符号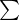 (读作sigma)
(读作sigma)
求和下限  :代表求和变量
:代表求和变量 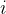 从1开始递增
从1开始递增
求和上限 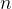 :代表递增到n结束
:代表递增到n结束
求和表达式 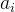 : 一般是通项公式(只不过是把通项下标符号从 n 换成 i 而已)
: 一般是通项公式(只不过是把通项下标符号从 n 换成 i 而已)
求和变量 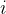 从1递增到n,则求和表达式
从1递增到n,则求和表达式 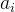 从
从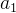 变化到
变化到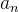
求和式整体即从 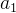 累加到
累加到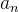 :
:
如果学过for循环就很好理解了
for(i=1; i<=n; i++)
{
sum+=a[i];
} 时 ,当前项
时 ,当前项  ,求和sum=
,求和sum= 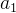 ,i++自增到2
,i++自增到2
 时 ,当前项
时 ,当前项  ,求和sum=
,求和sum=  ,i++自增到3
,i++自增到3
 时 ,当前项
时 ,当前项  ,求和sum=
,求和sum=  ,i++自增到4
,i++自增到4
……
 时 ,当前项
时 ,当前项  ,求和sum=
,求和sum=  ,i++自增到n
,i++自增到n
 时 ,当前项
时 ,当前项  ,求和sum=
,求和sum=  ,i++自增到n+1
,i++自增到n+1
 时,i<=n为假,循环结束
时,i<=n为假,循环结束
最终求和sum的值: 
二、等差、等比数列的求和式计算
【例1】等差数列 :1,2,3,……,n
:1,2,3,……,n
通项公式为  ,首项为1,公差为1
,首项为1,公差为1
根据上面得出的公式
代入得
这里的求和表达式 i 就是通项公式  (只不过是把通项下标符号从 n 换成 i 而已)
(只不过是把通项下标符号从 n 换成 i 而已)
反过来,已知求和式,就可以展开为多项式之和
求和变量 i 从1递增到n,求和表达式也是 i ,则整个求和式就是从1累加到n
根据等差数列前n项和公式 
可算出求和式的值为
即 
【例2】等比数列 :2,4,8,……,
:2,4,8,……,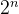
通项公式为  ,首项为2,公比为2
,首项为2,公比为2
数列前n项和,用求和式表达并展开
根据等比数列前n项和公式 
可算出求和式的值为
即 
三、求和式的线性规则之数乘规则
【例3】求和式 
其中求和表达式不是变量 ,而是常数1
展开求和式
因为求和表达式是常数1,不随求和变量 i 变化
所以一直是1在累加,n个1相加,结果自然是n
同理,如果求和表达式是2,n个2相加,结果是2n
同理,如果求和表达式是3,n个3相加,结果是3n
因为 ,如果把
,如果把  作为一个整体
作为一个整体
那么上面两式的结果可以替换为
可以看到,其实就是把常数提出来
提取常数可以理解为乘法分配律的逆运算
令a=1, b=1,将 c=2和c=3 分别代入得
只不过现在不是2项,而是n项
【例4】求和式 
当通项公式为变量时也同样适用
将常数提出,计算结果与上式相同
求和式的数乘规则(提取常数):
 (其中c为常数)
(其中c为常数)
注意,这里的常数c不一定是整数,也可以是小数
【例5】当  时,求和式
时,求和式 
四、求和式的线性规则之加法规则
【例6】求和式 
可以看到里面有两个通项公式,左边是等比数列,右边是等差数列
将其展开得
根据加法交换律,将等比数列的项都交换到左边,等差数列的项都交换到右边
可以看到,实际上就是两个数列分别求和再相加
将等式右边改写为求和式的形式
这就是求和式的加法规则(减法同理,减法就是特殊的加法)
如果要求值,则分别应用等比数列前n项和公式、等差数列前n项和公式
代入得求和式的值为
求和式的加法规则(减法同理):
如果不相信减法同理,也可以推理一遍
【例7】求和式 
五、求和多项式的分解
有了求和式的线性规则(数乘规则、加法规则),我们就有了分解求和多项式的依据
【例8】求和多项式 
首先使用数乘规则,将常数 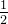 提出
提出
使用加法规则,将左边多项式先拆开
再使用加法规则,将右边多项式再拆开
改变形式,将 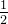 重新变回分母
重新变回分母
原式与结果对比
可以发现,其实就是对其中每一项分别应用求和运算
六、求和式的分段规则
【例9】再以等差数列 为例:1,2,3,……,n
为例:1,2,3,……,n
通项公式为  ,首项为1,公差为1
,首项为1,公差为1
假设数列中间有一个值m:1,2,3,…,m,(m+1),…,n
那么可以将数列求和分为两段:1—m 和 (m+1)—n
对前n项和进行展开
将等式右边分为两部分
再将等式右边转为求和式形式
求和式的分段规则
 (其中
(其中  )
)
如果将分段规则进行移项,可得下面两式,相当于逆用分段规则
而且分段规则也可以多次使用,举个简单例子
【例10】多项式 
或者直接代入已知求和式 
两种计算方式结果相同
七、求和式的上下限变换规则
【例11】有求和式1: 和 求和式2:
和 求和式2:
求和式1展开得
求和式2展开得
可见两式的值是相等的
你可能会疑惑,为什么求和式2也是100个1相加
如果反应不过来,可以将0—99同时+1
相当于在数轴上将0—99整体向右移1个单位,得到1—100,这肯定是100个
所以 
这就是常量求和式的上下限变换规则
对于变量来说,情况就不一样了
【例12】有求和式3: 和 求和式4:
和 求和式4:
求和式3展开得
求和式4展开得
可见两式的值是相等的
但是如果仿照上面,将求和式4的下标0—99同时+1
相当于在数轴上将0—99整体向右移1个单位,得到1—100
但是,此时得到的是  ,将其展开得
,将其展开得
可以发现上下限变换后,少了常数项0,多了常数项100
如果通项公式不随之改变,那么结果会发生变化
所以当求和上下限增加时,通项下标要相应减少
当求和上下限减少时,通项下标要相应增加
这样才能保证展开的多项式不变
这就是变量求和式的上下限变换规则
这里比较特殊,因为通项公式  ,所以
,所以 
【例13】求和式 
将其展开得
用上下限变换规则得
这里求和上下限减少(-1),通项下标要相应增加(+1)
因为通项公式  ,所以
,所以 
解法一:先用上下限变换规则,再展开计算
解法二:用数乘规则、分段规则(逆用)计算
解释一下,其中逆用分段规则进行分解
分解过程为
解法三:用数乘规则,上下限变换规则,加法规则计算
求和式的上下限变换规则
对于上下限变换规则的理解
【例14】有求和式  ,展开有n项
,展开有n项
对于这个求和式,变换原则就是无论 i 怎么变,都要让展开的多项式始终从 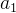 加到
加到 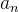
比如k=2时,求和上下限变换(+2),通项下标也对应变换(-2)
这样变换后展开的多项式与原式相同
另外,求和上下限的初始值不一定是1和n,这里只是一种简单表示
八、多重求和式计算
【例15】双重求和式 
可以类比复合函数,对右边加括号
先算括号内的 
上式变为
将其展开,即为等差数列求和
【例16】求和式 
在解决三重求和式之前,需要先推导出求和式  的值
的值
这里需要用到立方和公式、立方差公式、十字相乘法
①立方和公式:
特别地,当b=1时:
则 
②立方差公式:
特别地,当b=1时:
则 ![(n+1)^{3}-1^{3}=(n+1-1)[(n+1)^{2}+(n+1)+1]](https://latex.csdn.net/eq?%28n+1%29%5E%7B3%7D-1%5E%7B3%7D%3D%28n+1-1%29%5B%28n+1%29%5E%7B2%7D+%28n+1%29+1%5D)























 8万+
8万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








