内容提要
这篇博客的主要讲生成学习算法,主要包括两个算法:
- 高斯判别分析(Gaussian Discriminant Analysis)
- 朴素贝叶斯(Naive Bayes)
now let’s begin
前言
今天学习的生成学习算法依然属于监督式学习算法,我们需要输入训练集,训练参数,然后进行分类。比如我们输入动物的特征
x
,然后打上标签
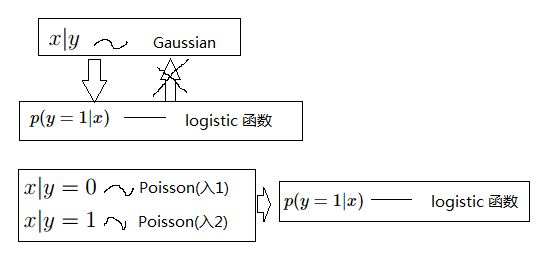
其中 p(x) 利用的是全概率公式: p(x)=p(x|y=1)p(y=1)+p(x|y=0)p(y=0) 。根据我们对这些特征分布的不同假设,就有了高斯判别分析和朴素贝叶斯。首先来看高斯判别分析:
高斯判别分析(Gaussian Discriminant Analysis)
高斯判别分析就是假设 p(x|y) 服从高斯分布,在实际情况中我们的 x 往往是一个向量。所以我们有必要先复习一下,多元高斯分布:
多元高斯分布
多元高斯分布中:
X 的期望为:
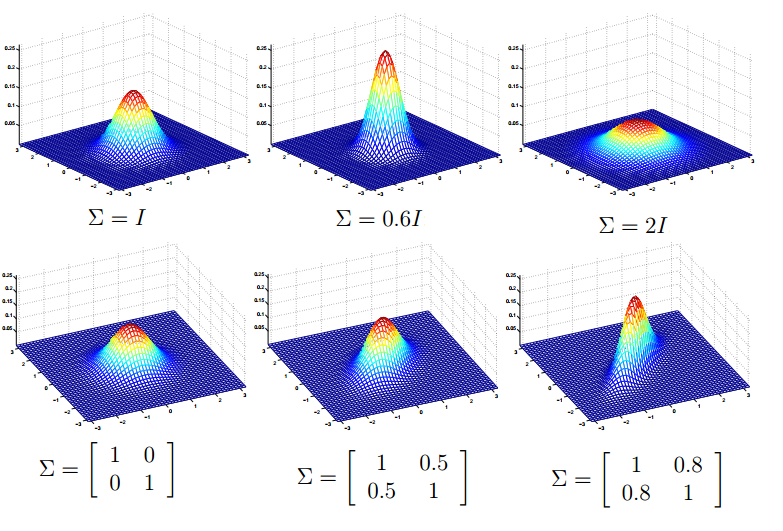
下面我们再来看看协方差矩阵和均值向量对密度函数的影响。首先看看协方差对密度函数的影响,如图示:
可以看出:
1. 协方差矩阵主对角线缩小图像就变得尖了,当增大时,图像就变得平摊了。
2. 协方差矩阵副对角线为正时,并且缩小,图像就以
y=x
为对称轴变扁。增大时,效果相反。
3. 协方差矩阵副对角线为负时,并且缩小,图像就一
y=−x
为对称轴变扁。增大时,效果相反。
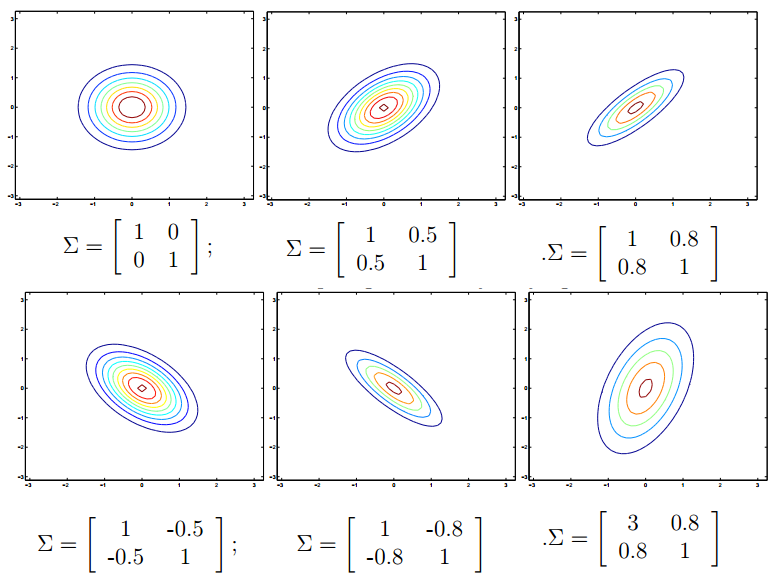
利用等高线图,可以更加清楚的看到这个性质:
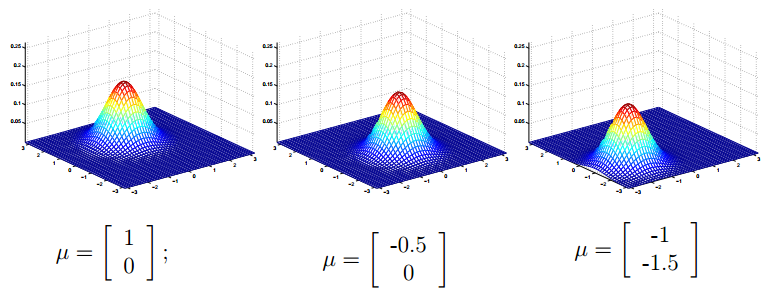
再来看看均值向量对密度函数的影响,如下图(协方差矩阵 ∑=I ):
总结起来,可以看出这种多元的高斯分布和一元的高斯分布非常类似。多元的均值向量影响的也是密度函数中心的位置,协方差矩阵影响的是密度函数的“胖瘦”。说是多元其实就是二元,更多元的我现在也不知道,因为,一元的时候是方差,二元的时候是协方差矩阵,那么三元的。。。我现在不知道,再看看。
高斯判别分析模型(Gaussian Discriminant Analysis model(简称GDA))
首先做出如下的假设,Andrew Ng老师在课上也没有解释为什么是这样的假设。我想可能是在实验中,做出这样的假设,得到的效果比较好。进而也将这种假设系统的设计成一种模型或者算法。
Andrew Ng老师解释说这不是条件概率,只是形式和他像。但是我就是像条件概率一样去理解他,也行。下来我们具体的写出它们的密度函数:
和之前一样,写出它的似然函数然后去对数(这个似然函数有一个转门的名字:Joint Likelihood):
然后令对数似然函数达到最大,利用之前的梯度上升,牛顿法都可以。但是对于这个式子具体的怎么推导我也不知道。Andrew Ng老师直接给出了,计算的结果。有了参数的就算结果,就可以让模型工作了。
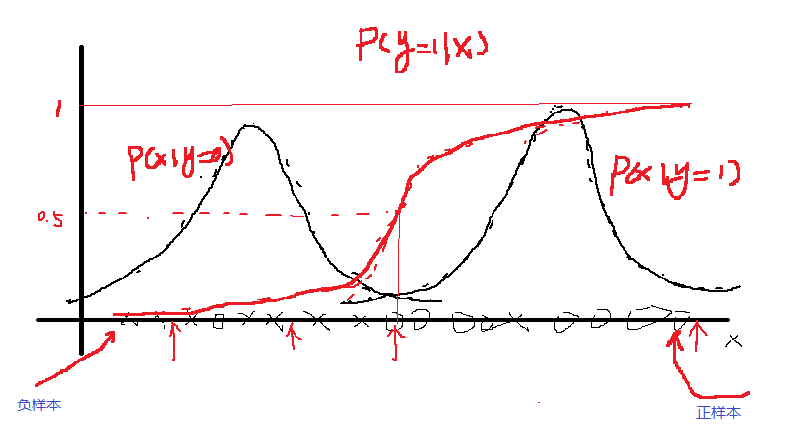
下来,我们看看一个简单的例子,一元的。如下图:
横坐标上的叉和圆圈都代表我们的输入特征,叉和圆圈仅仅是为了区分。你可以把他想象成狗和大象的特征。经过这些,数据的训练,我们就可以得到
ϕ,μ1,μ2,∑
的值。我们也就可以写出
p(x|y=0),p(x|y=1)
的密度表达式,图像分别为上图中左边和右边的高斯曲线。现在我们就可以利用这些参数计算
p(y=1|x)
的值,利用的公式是:
从左至右给出一些 x 就可得到相应的
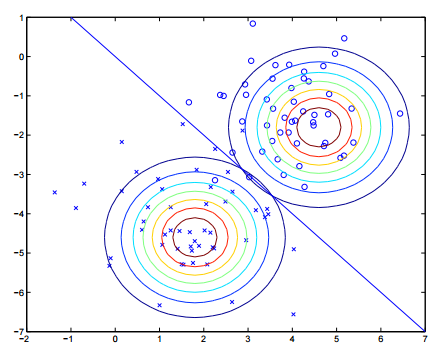
下面我们再来看看二维的分类效果:
这张图中高斯密度函数利用等高线绘制,最终我们得到了蓝色直线,它将两类分开。这就是高斯判别分析,写来是我们对高斯判别分析的讨论。
高斯判别分析的讨论
上图给出了一些关系,其实如果
朴素贝叶斯(Naive Bayes)
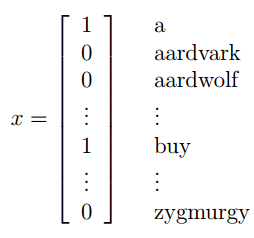
加入你现在有两百封邮件,需要去标记它是不是垃圾邮件
上图中右边单词或字母就是我们训练集中所有单词构成的字典。如果,一封邮件中出现了字典中的词,我们就在对应的特征位置标为1。但是,很容易想到词典的大小应该是一个很大的数,这就意味着我们特征向量的维数也是这个级别的或者更高,这就不是很好了。所以,朴素贝叶斯假设 xi 之间相互独立,即词典中各个词的出现没有关系。那么就可以写出 p(x|y) 的表达式,先利用条件概率的链式法则,再利用朴素贝叶斯的假设,就可以得到下面的式子:
条件概率链式规则的说明:
由 p(B|A)=p(AB)p(A) 可得 p(AB)=p(A)p(B|A)
同理先将AB看成一个整体: p(ABC)=p(AB)p(C|AB)=p(A)p(B|A)P(C|AB)Andrew Ng老师也大概给出了,怎么去生成字典,一种比较有效的方式:对于垃圾邮件,我们去遍历他,将其中出现3次的单词提取出来就得到了,我们的词典。也学你还有更好的方法。
从例子中可以看出:
p(x|y)∈{0,1}
,但是向量的维数特别高,因为他要和字典的维数一致。如果字典的维数为
n
,那么
特别的:朴素贝叶斯的假设一般不成立,比如出现了KFC就很可能出现buy,他们之间是有关系的。但是朴素贝叶斯在在实践中表现的很好,比如在邮件分类中。
下来我们要对各种情况的分布进行假设,我觉得这也是这两种生成学习算法的区别(不同分布的假设)。分布的假设是:伯努利分布,同时给出响应的参数:
如果我们有训练集 {x(i),y(i);i=1,2...m} ,此时我们就可以给出 joint 似然函数(joint likelihood)如下:
使得joint似然函数最大,便可以得到各个参数的似然估计,如下:
上式中
x(i)j
表示训练集中第
i
个特种向量
最终我们就可以得到判断垃圾邮件的响应函数,本质上就是一个贝叶斯公式:
其中对于
在来细细看看上面这个式子,我们发现它是一个分数的形式,这就需要考虑到分子为零情况。那么什么情况写分子才可能为零呢? p(y=1),p(y=0) 不可能同时为零,那么就要看看这些连乘的式子会不会为零,因为,连乘中只要有一个为零,整个式子就为零。想象一种情况,在我们训练好这个模型后,来了一封邮件,在它之中有一个词“NIPS”你的算法从来都没有见过,假如它出现的位置为35000处,由于之前从来都没有见过他,所以他既不是正常邮件,也不是垃圾邮件,所以训练的时候 x35000 这个的位置就是0,则得到的参数均为零:
在判断这封邮件时判断垃圾邮件的响应函数就出现了 00 的情况,怎么处理呢?Laplace smoothing
Laplace smoothing
我们先举个例子,比如一个球队的战绩:
| 时间 | 对手 | 比赛结果(0:失败) |
|---|---|---|
| 2/1 | A | 0 |
| 2/2 | B | 0 |
| 2/3 | C | 0 |
| 2/4 | D | 0 |
| 2/5 | E | ? |
求该对在与E对决中获胜的概率是多少?
p(y=1)=比赛结果“1”的个数+1比赛结果“1”的个数+1+比赛结果“0”的个数+1=16
这就是Laplace smoothing,我觉得他其中最关键的就是添加了“安全因子”,使得分母不为零。
对于朴素贝叶斯我们就可以做出如下改进:
|V| 是字典的维数。
再谈朴素贝叶斯
先来回顾一下,我们判断垃圾邮件的响应函数:
公式是这样写的,但是假如来了一封邮件,我们到底是怎样来判断他是否为垃圾邮件的?过程是这样的:来了一封邮件,我们得到了他的特征向量
x
,然后我们就利用上式进行计算,
对应下标,带入即可。最终响应函数可以进一步简写成如下样子:
其中 y∈{0,1} ,上式前后代换利用的是贝叶斯公式,由于有朴素假设,分布的和为1,所以就成了上面的样子。由于这个模型中 x,y 向量中的每一个分量的取值非0即1,所以这个模型称之为:多变量伯努利模型(multi-variate Bernoulli event model)
下来我们再来看看多项式模型(multinomial event model),在这个模型中,
x
的每一个分量
其中,
ni
为第i个特征向量
x
的维数。
最终分类的表达形式还可以表达成和上面的式子相同的样子:
参考资料
Andrew Ng老师的斯坦福公开课
end








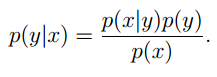
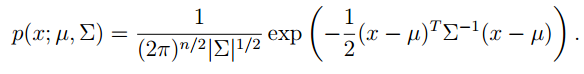
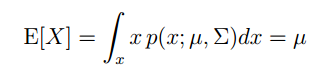
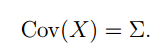
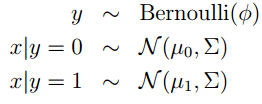
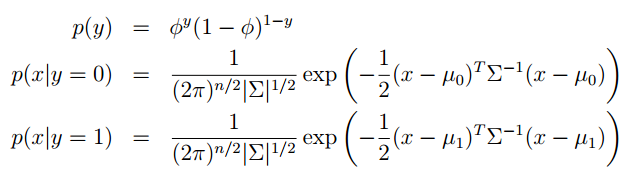
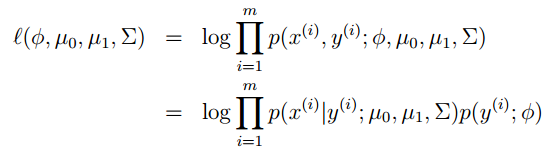

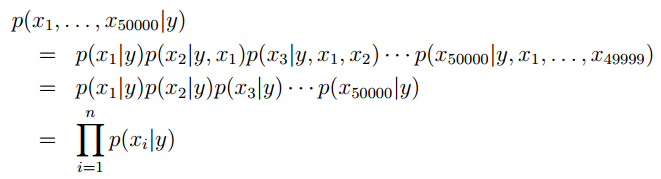
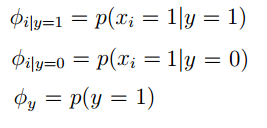
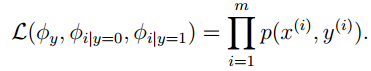

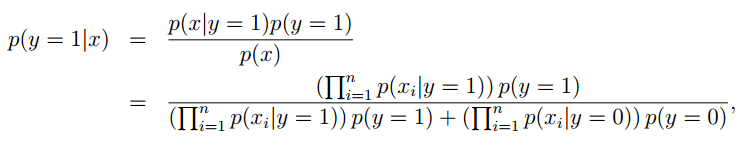
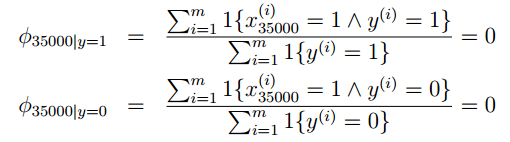
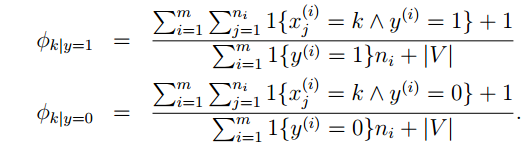
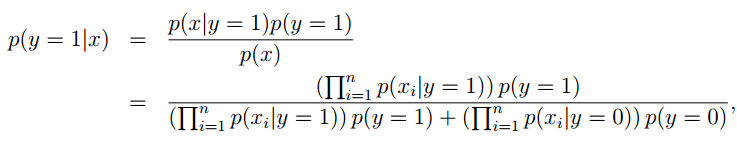
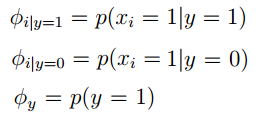
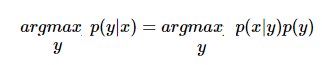
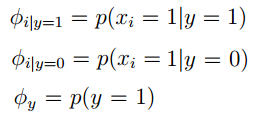
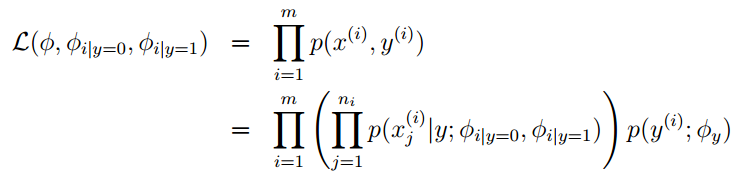
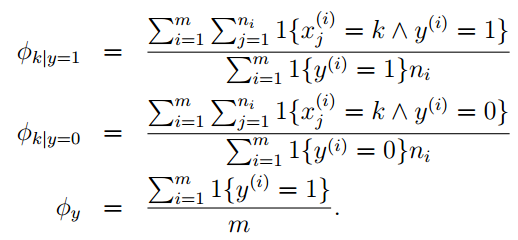
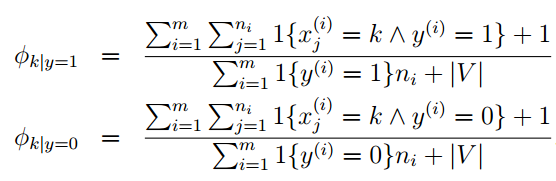
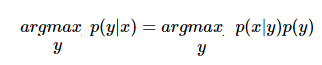














 4945
4945

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








