一 支持向量机基本型
间隔(Margin)与支持向量(Support Vector)
超平面方程:
w
T
x
+
b
=
0
w^Tx+b=0
wTx+b=0
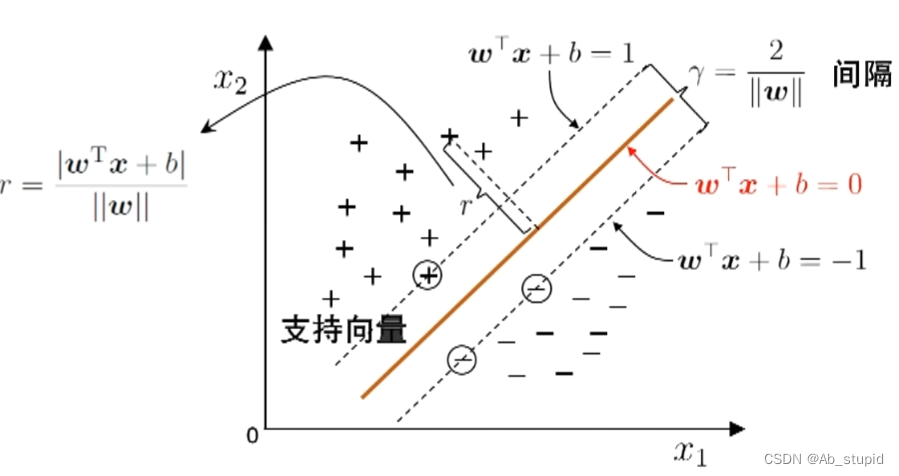 最大间隔: 寻找参数
w
w
w 和
b
b
b,使得
γ
γ
γ最大
最大间隔: 寻找参数
w
w
w 和
b
b
b,使得
γ
γ
γ最大
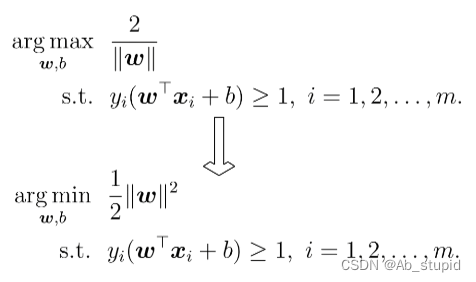
凸二次规划问题,能用优化计算包求解,但可以有更高效的办法(拉格朗日乘子法)
二 对偶问题与解的特性
1 对偶问题
第一步: 引入拉格朗日乘子
α
i
≥
0
\alpha_i≥0
αi≥0得到拉格朗日函数:
L
(
w
,
b
,
α
)
=
1
2
∣
∣
w
∣
∣
2
+
∑
i
=
1
m
α
i
(
1
−
y
i
(
w
r
x
i
+
b
)
)
L ( w , b , \alpha ) = \frac { 1 } { 2 } | | w | | ^ { 2 } + \sum _ { i = 1 } ^ { m } \alpha _ { i } ( 1 - y _ { i } ( w ^ { r } x _ { i } + b ) )
L(w,b,α)=21∣∣w∣∣2+i=1∑mαi(1−yi(wrxi+b))第二步: 令
L
(
w
,
b
,
α
)
L(w,b,\alpha)
L(w,b,α) 对
w
w
w 和
b
b
b 的偏导为零可得:
w
=
∑
i
=
1
m
a
i
j
y
i
x
i
,
0
=
∑
i
=
1
m
α
i
y
i
w = \sum _ { i = 1 } ^ { m } a _ { i j} y_i x _ { i } , \quad 0 = \sum _ { i = 1 } ^ { m } \alpha _ { i }y_i
w=i=1∑maijyixi,0=i=1∑mαiyi第三步: 回代可得:
m
a
x
α
∑
i
=
1
m
a
i
−
1
2
∑
i
=
1
m
∑
j
=
1
m
α
i
α
j
y
i
y
j
x
i
T
x
j
\operatorname { m a x _\alpha} \sum _ { i = 1 } ^ { m } a _ { i } - \frac { 1 } { 2 } \sum _ { i = 1 } ^ { m } \sum _ { j = 1 } ^ { m } \alpha_i\alpha_jy_iy_jx^T_ix_j
maxαi=1∑mai−21i=1∑mj=1∑mαiαjyiyjxiTxj
s
.
t
.
∑
i
=
1
m
a
i
y
i
=
0
,
a
i
≥
0
,
i
=
1
,
2
,
⋯
,
m
s.t.\quad \sum _ { i = 1 } ^ { m } a _ { i } y _ { i } = 0 , \quad a _ { i } \geq 0 , \quad i = 1 , 2 , \cdots , m
s.t.i=1∑maiyi=0,ai≥0,i=1,2,⋯,m
2 解的特性
最终模型:
f
(
x
)
=
w
T
x
+
b
=
∑
i
=
1
m
α
i
y
i
x
i
T
x
+
b
f ( x ) = w ^ { T } x + b = \sum _ { i = 1 } ^ { m }\alpha_iy_i x^T_i x + b
f(x)=wTx+b=∑i=1mαiyixiTx+b
KKT条件:
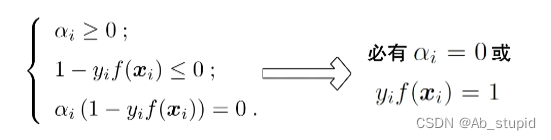
解的稀疏性: 训练完成后,最终模型仅与支持向量有关
3 求解方法-SMO
基本思路: 不断执行如下两个步骤直至收敛
- 第一步:选取一对需更新的变量 α i \alpha_i αi 和 α j \alpha_j αj
- 第二步:固定 α i \alpha_i αi 和 α j \alpha_j αj 以外的参数,求解对偶问题更新 α i \alpha_i αi 和 α j \alpha_j αj
仅考虑
α
i
\alpha_i
αi 和
α
j
\alpha_j
αj 时,对偶问题的约束
0
=
∑
i
=
1
m
a
i
y
i
0=\sum^m_{i=1}a_iy_i
0=∑i=1maiyi 变为:
α
i
y
i
+
α
j
y
j
=
c
,
α
i
≥
0
,
α
j
≥
0
\alpha _ { i } y _ { i } + \alpha _ { j } y _ { j } = c , \quad \alpha _ { i } \geq 0 , \quad \alpha _ { j } \geq 0
αiyi+αjyj=c,αi≥0,αj≥0用
a
i
a_i
ai 表示
a
j
a_j
aj,代入对偶问题有闭式解
m
a
x
α
∑
i
=
1
m
α
i
−
1
2
∑
i
=
1
m
∑
j
=
1
m
α
i
α
j
y
i
y
j
x
i
T
x
j
max_\alpha \sum _ { i = 1 } ^ { m } \alpha _ { i } - \frac { 1 } { 2 } \sum _ { i = 1 } ^ { m } \sum _ { j = 1 } ^ { m } \alpha_i\alpha_jy_iy_jx^T_ix_j
maxαi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxj对任意支持向量
(
x
s
,
y
s
)
(x_s,y_s)
(xs,ys) 有
y
s
f
(
x
s
)
=
1
y_sf(x_s)=1
ysf(xs)=1 由此可解出
b
b
b
为提高鲁棒性,通常使用所有支持向量求解的平均值
三 特征空间映射
若不存在一个能正确划分两类样本的超平面,怎么办?
将样本从原始空间映射到一个更高维的特征空间,使样本在这个特征空间内线性可分
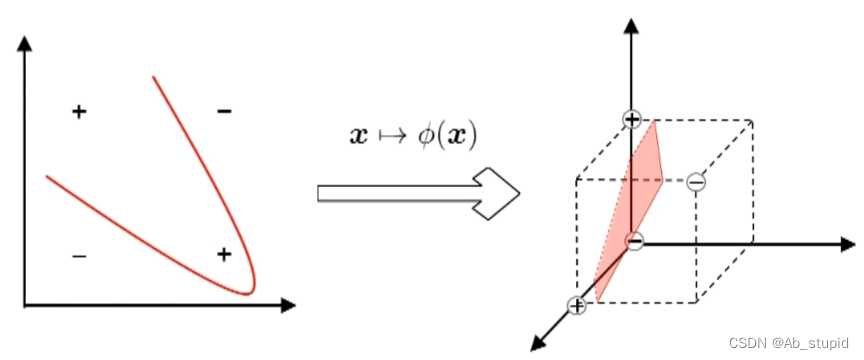
如果原始空间是有限维(属性数有限),那么一定存在一个高维特征空间使样本线性可分
在特征空间中

四 核函数(Kernel Function)
基本思路: 设计核函数
k
(
x
i
,
x
j
)
=
ϕ
(
x
i
)
T
ϕ
(
x
j
)
k ( x _ { i } , x _ { j } ) = \phi ( x _ { i } ) ^ { T } \phi ( x _ { j } )
k(xi,xj)=ϕ(xi)Tϕ(xj)
绕过显式考虑特征映射、以及计算高维内积的困难
Mercer 定理: 若一个对称函数所对应的核矩阵半正定,则它就能作为核函数来使用。
任何一个核函数,都隐式地定义了一个RKHS(Reproducing Kernel Hilbert Space,再生核希尔伯特空间)
“核函数选择”成为决定支持向量机性能的关键!
五 如何使用SVM解决自己特定的任务
1 以回归学习为例
基本思路: 允许模型输出与实际输出间存在
2
ε
2ε
2ε 的差别
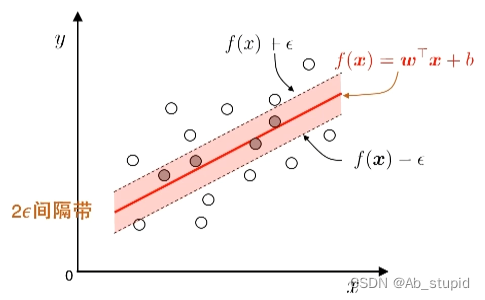
2 ε ε ε-不敏感损失函数
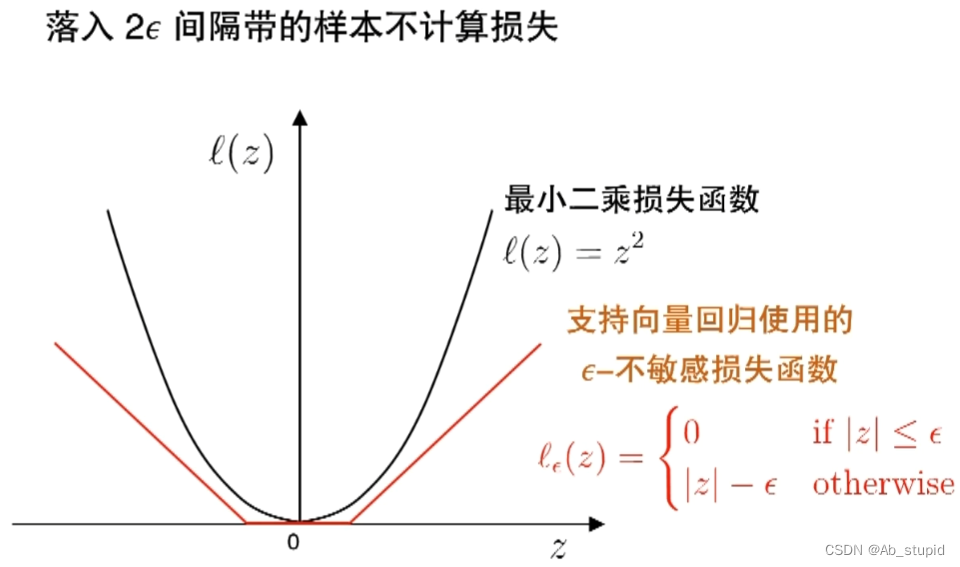
3 支持向量回归(SVR)

4 如何使用SVM
- 入门级——实现并使用各种版本SVM
- 专业级——尝试、组合核函数
- 专家级——根据问题而设计目标函数、替代损失、进而…





















 263
263











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








