考试大纲及考试内容
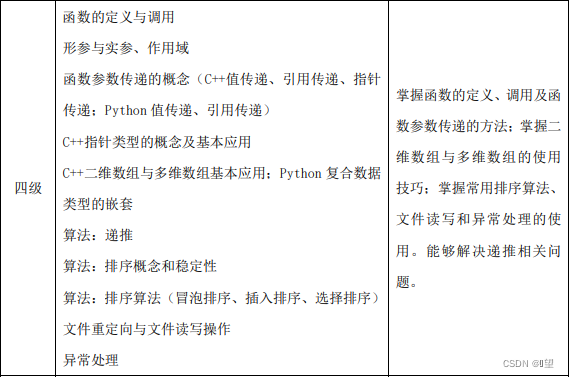
知识点复习
1.形参、实参、作用域
我们先来说形参和实参
定义:
形参:形参出现在函数定义中,在整个函数体内都可以使用,离开该函数则不能使用。
实参:实参出现在主调函数中,进入被调函数后,实参变量也不能使用。
网上很多大佬都是这么讲的,但我还是认为举个例子更容易理解:
假设我定义了这样一个函数
int f(int x){
return 0;
}
然后我在主函数中这么调用它
int main(){
int n;
f(n);
return 0;
}
- 那么
int f(int x)中的 x x x就是形参(在函数中定义,并只能在此函数中使用的参数) - 主函数中
f(n)的 n n n就是实参(将数据传入函数中的参数)
————————————————————————
我们再来说说作用域
作用域,顾名思义,就是变量或常量的作用范围(可使用范围)
for(int i = 1; i <= n; i++)
cout << k;//这句话的作用域就是当前行,仅在当前行执行
for(int i = 1; i <= n; i++){
……
cout << k;//加入花括号后,这句话的作用范围就变到了这个for循环语句内,即两个花括号以内
……
}
2.函数的定义和调用
int(返回值类型) f(自定义函数名) (int x(形参列表)){
主体
return x(表达式);
}
- 返回值类型 :一个函数可以返回一个值的类型
- 函数名:给函数起的自定义名称
- 参数列表:使用该函数时,传入的数据
- 函数体语句:花括号内的代码,函数内需要执行的语句
- return表达式: 和返回值类型挂钩,函数执行完后,返回相应的数据
排序的概念和稳定性
| 排序算法 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 冒泡排序 | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 插入排序 | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 选择排序 | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
文件重定向与文件读写
freopen("a.in","r",stdin)//将输入重定向为从文件a.in读入
freopen("a.out","w",stdout)//将输出重定向为从输出到文件a.out中
//下面的程序任然使用标准输入输出(scanf,printf)
#include<fstream>
ifstream cin("a.in");//在main()函数里定义较好
ofsteam cout("a.out");
//下面标准输入输出








 本文介绍了编程中的基本概念,包括形参与实参的区别,强调了它们在函数调用中的角色。此外,还讨论了变量的作用域,以示例说明了局部作用域和块级作用域。同时,提到了函数的定义与调用的语法,并列举了几种排序算法的时间和空间复杂度,以及稳定性。最后,文章讲解了文件重定向和文件读写的基本操作。
本文介绍了编程中的基本概念,包括形参与实参的区别,强调了它们在函数调用中的角色。此外,还讨论了变量的作用域,以示例说明了局部作用域和块级作用域。同时,提到了函数的定义与调用的语法,并列举了几种排序算法的时间和空间复杂度,以及稳定性。最后,文章讲解了文件重定向和文件读写的基本操作。
















 3033
3033

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








