参考:
- https://zhuanlan.zhihu.com/p/47185756
- https://zhuanlan.zhihu.com/p/494536555
- https://zhuanlan.zhihu.com/p/465921554
- https://zhuanlan.zhihu.com/p/91652813
- https://zhuanlan.zhihu.com/p/89614607
Boosting 思想
Boosting模型可以抽象为一个前向加法模型(additive model): F ( x ; α m , θ m ) = ∑ m = 1 M α m f ( x ; θ m ) F(x;{\alpha_{m}, \theta_{m}})=\sum_{m=1}^{M}\alpha_{m}f(x;\theta_{m}) F(x;αm,θm)=∑m=1Mαmf(x;θm)
其中, x 为输入样本, f ( x ; θ m ) f(x;\theta_{m}) f(x;θm) 为每个基学习器, θ m \theta_{m} θm为每个基学习器的参数,treeBoost论文里面讨论的基学习器都是CART回归树。Boost是"提升"的意思,一般Boosting算法都是一个迭代的过程,每一次新的训练都是为了改进上一次的结果,这要求每个基学习器的方差足够小(稳定),即足够简单(模型参数足够简单,不会导致过拟合)(weak machine),因为Boosting的迭代过程足以让bias减小,但是不能减小方差。(Bagging的基分类器是偏差小方差大,而boosting的基分类器是偏差大方差小)
Boosting模型是通过最小化损失函数得到最优模型的,这是一个NP难问题,一般通过贪心法在每一步贪心地得到最优的基学习器。可以通过梯度下降的带每个最优基学习器的方向!
过去我们使用的梯度下降都是在参数空间的梯度下降,变量是参数,而Boosting算法是在函数空间的梯度下降。通过不断梯度下降,我们得到很多个基学习器(函数),将每个阶段得到的基学习器相加得到最终的学习器。直观地说,当前基学习器的训练需要知道所有学习器在每一个样本上的表现都差了多少,然后当前基学习器努力地学习如何将每个样本上差了的部分给补充上来。回忆一下,之前在调模型参数的时候,我们通过梯度下降知道每个参数与下一个可能的loss最小的点都差了多少,根据这个信息去更新参数.
在梯度下降法中,我们可以看出,对于最终的最优解
θ
∗
\theta^*
θ∗,是由初始值
θ
0
\theta_{0}
θ0经过T次迭代之后得到的,这里设
θ
0
=
−
δ
L
(
θ
)
δ
θ
0
\theta_0=-\frac{\delta L(\theta)}{\delta \theta_0}
θ0=−δθ0δL(θ) ,则
θ
∗
\theta^*
θ∗为:
θ
∗
=
∑
t
=
0
T
α
t
∗
[
−
δ
L
(
θ
)
δ
θ
]
θ
=
θ
t
−
1
=
θ
T
−
1
+
α
T
[
−
δ
L
(
θ
)
δ
θ
]
θ
=
θ
T
−
1
\theta^*=\sum_{t=0}^T \alpha_t *\left[-\frac{\delta L(\theta)}{\delta \theta}\right]_{\theta=\theta_{t-1}}=\theta_{T-1}+\alpha_T\left[-\frac{\delta L(\theta)}{\delta \theta}\right]_{\theta=\theta_{T-1}}
θ∗=t=0∑Tαt∗[−δθδL(θ)]θ=θt−1=θT−1+αT[−δθδL(θ)]θ=θT−1
其中, [ − δ L ( θ ) δ θ ] θ = θ t − 1 \left[-\frac{\delta L(\theta)}{\delta \theta}\right]_{\theta=\theta_{t-1}} [−δθδL(θ)]θ=θt−1 表示 θ \theta θ 在 θ − 1 \theta-1 θ−1 处泰勒展开式的一阶导数。
在函数空间中,我们也可以借鉴梯度下降的思想,进行最优函数的搜索。对于模型的损失函数 L ( y , F ( x ) ) L(y,F(x)) L(y,F(x)) ,为了能够求解出最优的函数 F ∗ ( x ) F^*(x) F∗(x) ,首先设置初始值为: F 0 ( x ) = f 0 ( x ) F_0(x)=f_0(x) F0(x)=f0(x)
以函数 F(x)作为一个整体,与梯度下降法的更新过程一致,假设经过T次迭代得到最优的函数
F
∗
(
x
)
F^*(x)
F∗(x) 为:
F
∗
(
x
)
=
∑
t
=
0
T
f
t
(
x
)
=
F
T
−
1
(
x
)
+
f
T
(
x
)
F^*(x)=\sum_{t=0}^T f_t(x)=F_{T-1}(x)+f_T(x)
F∗(x)=t=0∑Tft(x)=FT−1(x)+fT(x)
其中,
f
T
(
x
)
f_T(x)
fT(x) 为:
f
t
(
x
)
=
−
α
t
g
T
(
x
)
=
−
α
T
∗
[
δ
L
(
y
,
F
(
x
)
)
δ
F
(
x
)
]
F
(
x
)
=
F
T
−
1
(
x
)
f_t(x)=-\alpha_t g_T(x)=-\alpha_T *\left[\frac{\delta L(y, F(x))}{\delta F(x)}\right]_{F(x)=F_{T-1}(x)}
ft(x)=−αtgT(x)=−αT∗[δF(x)δL(y,F(x))]F(x)=FT−1(x)

总结:Gradient Boosting算法在每一轮迭代中,首先计算出当前模型在所有样本上的负梯度,然后以该值为目标训练一个新的弱分类器进行拟合并计算出该弱分类器的权重,最终实现对模型的更新。
注意:决策树是启发式算法,因为它通过递归地进行特征选择和判定,以达到最终的决策结果。在每个节点上,它选择最能区分数据的特征进行分割,通过对数据集的分层判断,最终形成一个树状结构。
函数空间
定义:对于每一个特征x,都有一个函数数值F(x)与之对应,函数空间的指标就是这些函数数值F(x),因此函数空间有无数个坐标,但是在训练过程,一般只有有限个训练样本(x),因此函数空间的维度也是有限的 F ( x i ) 1 N {F(x_{i})}^{N}_{1} F(xi)1N 。
在函数空间里面做gradient descent,相当求出函数在每个样本函数值方向上的梯度,即: g m ( x i ) = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) g_{m}(x_{i})=-[\frac{\partial L(y_{i}, F(x_{i}))}{\partial F(x_{i})}]_{F(x)=F_{m-1}(x)} gm(xi)=−[∂F(xi)∂L(yi,F(xi))]F(x)=Fm−1(x);
但是,这个负梯度只是定义在有限的训练样本支撑起的函数空间里面,如果泛化到其他的数据点呢, 这个基学习器在训练样本上的取值尽可能拟合负梯度,以AdaBoost为例,负梯度为:
g m ( x i ) = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) = y i e − y i F m − 1 ( x ) i g_{m}(x_{i})=-[\frac{\partial L(y_{i}, F(x_{i}))}{\partial F(x_{i})}]_{F(x)=F_{m-1}(x)}=y_{i}e^{-y_{i}F_{m-1}(x)_{i}} gm(xi)=−[∂F(xi)∂L(yi,F(xi))]F(x)=Fm−1(x)=yie−yiFm−1(x)i
其中** e − y i F m − 1 ( x i ) e^{-y_{i}F_{m-1}(x_{i})} e−yiFm−1(xi)可以理解为样本的权重**,如果样本在之前几轮的分类都正确,即 y i = F m − 1 ( x i ) = 1 ( o r − 1 ) y_{i} =F_{m-1}(x_{i})=1 (or -1) yi=Fm−1(xi)=1(or−1),则 e − y i F m − 1 ( x i ) e^{-y_{i}F_{m-1}(x_{i})} e−yiFm−1(xi)会比较小;反之,权重( e − y i F m − 1 ( x i ) e^{-y_{i}F_{m-1}(x_{i})} e−yiFm−1(xi),上一轮迭代计算得到的系数)很大,本轮的基学习器需要在这个样本上得到较大的数值才能把这个样本从错误的泥潭拉回来。要是基学习器( f m ( X ) f_m(X) fm(X))拟合好负梯度==(即 f m ( X ) ∙ g m ( X ) f_{m}(X) \bullet g_{m}(X) fm(X)∙gm(X))==,即要求基学习器在各个样本上的函数值(这里写成了向量X形式)与负梯度的点积最大,即:
m a x ∑ i = 1 N f m ( x i ) y i e − y i F m − 1 ( x i ) = m i n ∑ i N I ( h t ( x i ) ≠ y i ) e − y i F m − 1 ( x i ) max \sum_{i=1}^{N}f_m(x_{i})y_{i}e^{-y_{i}F_{m-1}(x_{i})}=min \sum_{i}^{N}I(h_{t}(x_{i}) \ne y_{i})e^{-y_{i}F_{m-1}(x_{i})} max∑i=1Nfm(xi)yie−yiFm−1(xi)=min∑iNI(ht(xi)=yi)e−yiFm−1(xi)
分析:
- 等号左边:因为要满足基学习器拟合负梯度,也就是让基分类器的结果去靠近负梯度,而左边的式子可以写成点积形式 f m ( X ) ∙ y T e y T ∙ F m − 1 ( X ) , 其中 X = ( x 1 , . . . , x n ) , y = ( y 1 , . . . , y n ) f_{m}(X) \bullet y^{T}e^{y^T \bullet F_{m-1}(X)},其中X=(x_{1},...,x_{n}), y=(y_{1}, ..., y_{n}) fm(X)∙yTeyT∙Fm−1(X),其中X=(x1,...,xn),y=(y1,...,yn),此时好的拟合效果就是保证点积左右的向量最好是同向,也就是保证点积式子max
- 而左边的式子其实可以分为 h t ( x i ) = y i h_{t}(x_{i})=y_{i} ht(xi)=yi和 h t ( x i ) ≠ y i h_{t}(x_{i})\ne y_{i} ht(xi)=yi,要保证左边式子最大化,也就是最小化 h t ( x i ) ≠ y i h_{t}(x_{i})\ne y_{i} ht(xi)=yi(这个在 ∑ i = 1 N h t ( x i ) y i e − y i F m − 1 ( x i ) \sum_{i=1}^{N}h_{t}(x_{i})y_{i}e^{-y_{i}F_{m-1}(x_{i})} ∑i=1Nht(xi)yie−yiFm−1(xi)占比最大)
求出负梯度的目的是为给下一个基学习器的学习指明方向,下一个基学习器的学习目标就是拟合这些负梯度(重点关注负梯度比较大的样本)。如果loss在某个样本函数值上的负梯度大于0(则说明y=1),也说明在下一个基学习器应该增加在这个样本上的函数值([负梯度>0] => [Cost关于F(x)的梯度<0] => [满足 e − x e^{-x} e−x单调性] => [ y i F m − 1 ( x i ) y_{i}F_{m-1}(x_{i}) yiFm−1(xi)向x正半轴移动(y=1)] 。
对梯度提升算法的若干思考
- 梯度提升与梯度下降的区别和联系是什么?
可以发现,两者都是在每一轮迭代中,都是利用损失函数相对于模型的负梯度方向的信息来对当前模型进行更新,只不过在梯度下降中,模型是以参数化形式表示,从而模型的更新等价于参数的更新。而在梯度提升中,模型并不需要进行参数化表示,而是直接定义在函数空间中,从而大大扩展了可以使用的模型种类。
- 梯度提升和提升树算法的区别和联系?
当损失函数是平方误差损失函数和指数损失函数时,每一步优化是很简单的。但对一般损失函数而言,往往每一步优化并不那么容易。针对这一问题,Freidman提出了梯度提升(gradient boosting)算法。这是利用损失函数的负梯度在当前模型的值 − [ δ L ( y , F ( x ) ) δ F ( x ) ] F ( x ) = F t − 1 ( x ) -\left[\frac{\delta L(y, F(x))}{\delta F(x)}\right]_{F(x)=F_{t-1}(x)} −[δF(x)δL(y,F(x))]F(x)=Ft−1(x) 作为提升树算法中残差的近似值,拟合一个梯度提升模型。
- 对于一般损失函数而言,为什么可以利用损失函数的负梯度在当前模型的值作为梯度提升算法中残差的近似值呢?
我们观察到在提升树算法中,残差 y − F ( x ) y-F(x) y−F(x) 是损失函数 1 2 ( y − F ( x ) ) 2 \frac{1}{2}(y-F(x))^2 21(y−F(x))2的负梯度方向,因此可以将其推广到其他不是平方误差(分类或是排序问题)的损失函数。也就是说,梯度提升算法是一种梯度下降算法,不同之处在于更改损失函数和求其负梯度就能将其推广。即:可以将结论推广为对于一般损失函数也可以利用损失函数的负梯度近似拟合残差。
损失函数
主要是要采用一种贪心的策略,找到使得loss最小的基学习器作为当前的基学习器:
loss function: a r g m i n α , θ = ∑ i = 1 N L ( y i , F m − 1 ( x i ) + α f m ( x i ; θ ) ) argmin_{\alpha, \theta}=\sum_{i=1}^{N}L(y_{i}, F_{m-1}(x_{i})+\alpha f_{m}(x_{i}; \theta)) argminα,θ=∑i=1NL(yi,Fm−1(xi)+αfm(xi;θ))
其中: θ \theta θ 是第m轮的基学习器的参数, α \alpha α 是学习的步长
探究loss function 与拟合负梯度的联系(从三个方面):
理解层面:负梯度的方向是loss下降的最快的方向,因此拟合好负梯度其实等价于让loss下降的最多
一阶泰勒展开
因为boosting的目标是让 L ( y i , F m ( x i ) ) ≤ L ( y i , F m − 1 ( x i ) ) , 而 L ( y i , F m ( x i ) ) = L ( y i , F m − 1 ( x i ) + α f m ( x i ; θ ) ) L(y_{i}, F_{m}(x_{i})) \le L(y_{i}, F_{m-1}(x_{i})), 而L(y_{i}, F_{m}(x_{i}))=L(y_{i}, F_{m-1}(x_{i})+\alpha f_{m}(x_{i}; \theta)) L(yi,Fm(xi))≤L(yi,Fm−1(xi)),而L(yi,Fm(xi))=L(yi,Fm−1(xi)+αfm(xi;θ)),所以 L ( y i , F m ( x i ) ) − L ( y i , F m − 1 ( x i ) ) = L ( y i , α f m ( x i ; θ ) ) L(y_{i}, F_{m}(x_{i})) - L(y_{i}, F_{m-1}(x_{i})) = L(y_{i}, \alpha f_{m}(x_{i}; \theta)) L(yi,Fm(xi))−L(yi,Fm−1(xi))=L(yi,αfm(xi;θ))(满足L(a, b+c) = L(a, b) + L(a, c));(因为对于交叉熵损失函数无法满足L(a, b+c) = L(a, b) + L(a, c));
因为
∑ i = 1 N L ( y i , F m − 1 ( x i ) + α f m ( x i ; θ ) ) ≈ ∑ i = 1 N L ( y i , F m − 1 ( x i ) ) + ∑ i = 1 N ∂ L ( y , F ( x ) ) ∂ F ( x ) ∣ F ( x ) = F m − 1 ( x i ) α f m ( x i ; θ ) ∑ i = 1 N L ( y i , F m − 1 ( x i ) + α f m ( x i ; θ ) ) − ∑ i = 1 N L ( y i , F m − 1 ( x i ) ) ≈ ∑ i = 1 N ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ∣ F ( x i ) = F m − 1 ( x i ) α f m ( x i ; θ ) ( 不等号右边可以看成两个向量的内积: ∂ L ( y , F ( X ) ) ∂ F ( X ) 和 α f m ( X ) , 其中 X = ( x 1 , x 2 , . . . , x n ) T , y = ( y 1 , y 2 , . . . , y n ) T 当 α f m ( x i ; θ ) = − ∑ i = 1 N ∂ L ( y i , F ( x ) ) ∂ F ( x ) ∣ F ( x ) = F m − 1 ( x i ) (梯度的负方向是局部下降最快的方向)时, ∑ i = 1 N L ( y i , F m − 1 ( x i ) + α f m ( x i ; θ ) ) − ∑ i = 1 N L ( y i , F m − 1 ( x i ) ) ≤ 0 \sum_{i=1}^{N}L(y_{i}, F_{m-1}(x_{i})+\alpha f_{m}(x_{i}; \theta)) \approx\sum_{i=1}^{N}L(y_{i}, F_{m-1}(x_{i}))+\sum_{i=1}^{N} \frac{\partial L(y, F(x))}{\partial F(x)}|_{F(x)=F_{m-1}(x_{i})}\alpha f_{m}(x_{i}; \theta)\\ \sum_{i=1}^{N}L(y_{i}, F_{m-1}(x_{i})+\alpha f_{m}(x_{i}; \theta)) - \sum_{i=1}^{N}L(y_{i}, F_{m-1}(x_{i})) \approx\sum_{i=1}^{N} \frac{\partial L(y_{i}, F(x_{i}))}{\partial F(x_{i})}|_{F(x_{i})=F_{m-1}(x_{i})}\alpha f_{m}(x_{i}; \theta)\\ (不等号右边可以看成两个向量的内积: \frac{\partial L(y, F(X))}{\partial F(X)}和\alpha f_{m}(X),其中X=(x_{1}, x_{2},...,x_{n})^{T}, y=(y_{1}, y_{2},...,y_{n})^{T}\\ 当\alpha f_{m}(x_{i}; \theta) = - \sum_{i=1}^{N} \frac{\partial L(y_{i}, F(x))}{\partial F(x)}|_{F(x)=F_{m-1}(x_{i})}(梯度的负方向是局部下降最快的方向)时,\\ \sum_{i=1}^{N}L(y_{i}, F_{m-1}(x_{i})+\alpha f_{m}(x_{i}; \theta)) - \sum_{i=1}^{N}L(y_{i}, F_{m-1}(x_{i})) \le 0 i=1∑NL(yi,Fm−1(xi)+αfm(xi;θ))≈i=1∑NL(yi,Fm−1(xi))+i=1∑N∂F(x)∂L(y,F(x))∣F(x)=Fm−1(xi)αfm(xi;θ)i=1∑NL(yi,Fm−1(xi)+αfm(xi;θ))−i=1∑NL(yi,Fm−1(xi))≈i=1∑N∂F(xi)∂L(yi,F(xi))∣F(xi)=Fm−1(xi)αfm(xi;θ)(不等号右边可以看成两个向量的内积:∂F(X)∂L(y,F(X))和αfm(X),其中X=(x1,x2,...,xn)T,y=(y1,y2,...,yn)T当αfm(xi;θ)=−i=1∑N∂F(x)∂L(yi,F(x))∣F(x)=Fm−1(xi)(梯度的负方向是局部下降最快的方向)时,i=1∑NL(yi,Fm−1(xi)+αfm(xi;θ))−i=1∑NL(yi,Fm−1(xi))≤0
在GBDT中,会令 r x i , y i = r m i = − ∂ L ( y i , F ( x ) ) ∂ F ( x ) ∣ F ( x ) = F m − 1 ( x i ) r_{x_{i}, y_{i}}=r_{mi}=-\frac{\partial L(y_{i}, F(x))}{\partial F(x)}|_{F(x)=F_{m-1}(x_{i})} rxi,yi=rmi=−∂F(x)∂L(yi,F(x))∣F(x)=Fm−1(xi)
总结GBDT的整体流程:
- 计算当前损失函数的负梯度表达式(训练样本的权值或概率分布);
- 构造训练样本将 ( x i , y i ) (x_{i}, y_{i}) (xi,yi)带入 r m ( x , y ) r_{m}(x, y) rm(x,y)可得到 r m i r_{mi} rmi,进而得到第m轮的训练样本为 T m = ( x 1 , r m 1 ) , . . . , ( x N , r m N ) T_{m}={(x_{1},r_{m1}), ...,(x_{N}, r_{mN})} Tm=(x1,rm1),...,(xN,rmN)
- 让当前基学习器去拟合上述训练样本得到 α f m ( x i , θ ) \alpha f_{m}(x_{i}, \theta) αfm(xi,θ)

伪代码:

注:
-
首先初始化第0个基学习器 F 0 ( x ) = a r g m i n c ∑ i = 1 N L ( y i , c ) F_{0}(x)=argmin_{c}\sum_{i=1}^{N}L(y_{i},c) F0(x)=argminc∑i=1NL(yi,c),即对于每一个x,第0个基学习器是使得当前loss最小的一个数值,第4行计算当前基学习器参数的时候,用了平方误差衡量基学习器与负梯度的拟合程度,实际应该根据问题选择相应的loss
-
探究算法的第1步 F 0 ( x ) = arg min ρ ∑ i = 1 N L ( y i , ρ ) F_0(\mathbf{x})=\arg \min _\rho \sum_{i=1}^N L\left(y_i, \rho\right) F0(x)=argminρ∑i=1NL(yi,ρ)
-
当损失函数为均方误差时, F 0 ( x ) = y ˉ ( 样本真实值的平均值 ) F_0(x)=\bar{y}(样本真实值的平均值) F0(x)=yˉ(样本真实值的平均值)
-
当损失函数为MAE时, F 0 ( x ) = m e d i a n y ( 样本真实值的中位数 ) F_0(x)=median_{y}(样本真实值的中位数) F0(x)=mediany(样本真实值的中位数)
M A E = 1 m ∑ i = 1 m ∣ c − y i ∣ MAE = \frac{1}{m} \sum_{i=1}^m \mid c-y_i \mid MAE=m1∑i=1m∣c−yi∣, g r a d i e n t o f M A E = 1 m ∑ i = 1 m s i g n ( c − y i ) = 0 gradient\ of MAE = \frac{1}{m} \sum_{i=1}^msign(c-y_i)=0 gradient ofMAE=m1∑i=1msign(c−yi)=0,也就是说,对于所有的样本真实值 { y i } 1 N \left \{y_i\right \}_1^N {yi}1N,要满足 c > y i 和 c < y i c>y_i和c<y_i c>yi和c<yi一样多,只能是c为中位数。(如果样本x在样本中的label取值为2, 4, 6,9,那么在 MAE 下训练的模型预估值应该是中位数5)
-
当损失函数为logistic loss时, F 0 ( x ) = ( 1 2 ) ∗ log ( ∑ y i ∑ ( 1 − y i ) ) \mathrm{F}_0(\mathrm{x})=\left(\frac{1}{2}\right) * \log \left(\frac{\sum \mathrm{y}_{\mathrm{i}}}{\sum\left(1-\mathrm{y}_{\mathrm{i}}\right)}\right) F0(x)=(21)∗log(∑(1−yi)∑yi)

-
当损失函数为指数函数 L ( y i , F ( x i ) ) = e − y i F ( x i ) , F 0 ( x ) = 1 2 l o g ∑ i = 1 N I ( y i = 1 ) ∑ i = 1 N I ( y i = − 1 ) \mathrm{L}\left(\mathrm{y}_{\mathrm{i}}, \mathrm{F}\left(\mathrm{x}_{\mathrm{i}}\right)\right)=\mathrm{e}^{-\mathrm{y_i}F\left(\mathrm{x}_{\mathrm{i}}\right)},F_0(x)=\frac{1}{2}log\frac{\sum_{i=1}^NI(y_i=1)}{\sum_{i=1}^NI(y_i=-1)} L(yi,F(xi))=e−yiF(xi),F0(x)=21log∑i=1NI(yi=−1)∑i=1NI(yi=1)
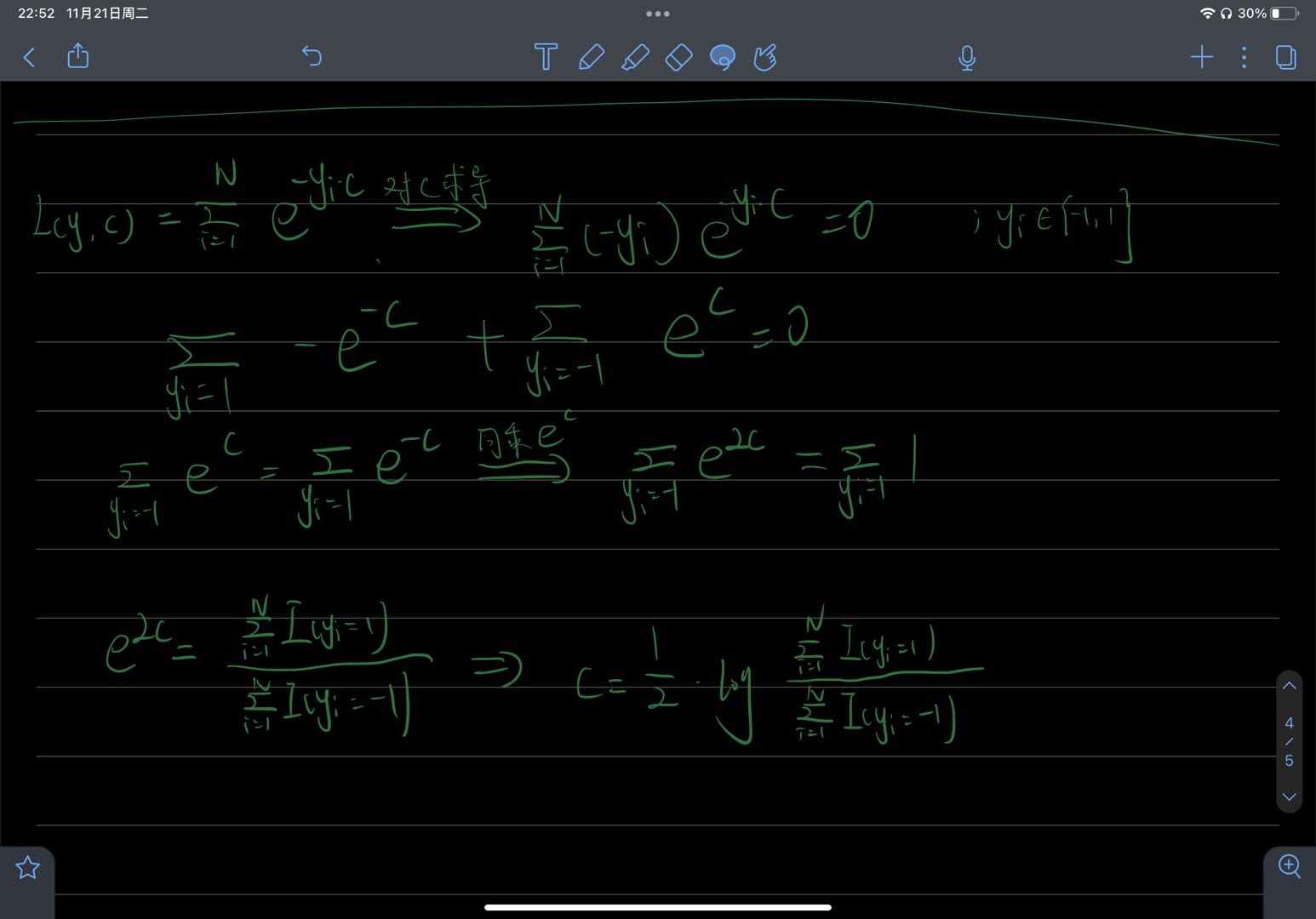
-
-
探究算法的第3步 y ~ i = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F m − 1 ( x ) \tilde{\mathrm{y}}_{\mathrm{i}}=-\left[\frac{\partial \mathrm{L}\left(\mathrm{y}_{\mathrm{i}}, \mathrm{F}\left(\mathrm{x}_{\mathrm{i}}\right)\right)}{\partial \mathrm{F}\left(\mathrm{x}_{\mathrm{i}}\right)}\right]_{\mathrm{F}(\mathrm{x})=\mathrm{F}_{\mathrm{m}-1}(\mathrm{x})} y~i=−[∂F(xi)∂L(yi,F(xi))]F(x)=Fm−1(x)
-
当损失函数采用 L ( y i , F ( x i ) ) = 1 2 ( y i − F ( x i ) ) 2 L(y_i, F(x_i))=\frac{1}{2}(y_i-F(x_i))^2 L(yi,F(xi))=21(yi−F(xi))2,那么负梯度为 y i − F ( x i ) y_i-F(x_i) yi−F(xi),将 F ( x i ) = F m − 1 ( x i ) F(x_i)=F_{m-1}(x_i) F(xi)=Fm−1(xi)带入结果得到 y i − F m − 1 ( x i ) y_i-F_{m-1}(x_i) yi−Fm−1(xi)
-
当损失函数采用 L ( y i , F ( x i ) ) = ∣ y i − F ( x i ) ∣ L(y_i, F(x_i))=|y_i-F(x_i)| L(yi,F(xi))=∣yi−F(xi)∣,那么其负梯度为
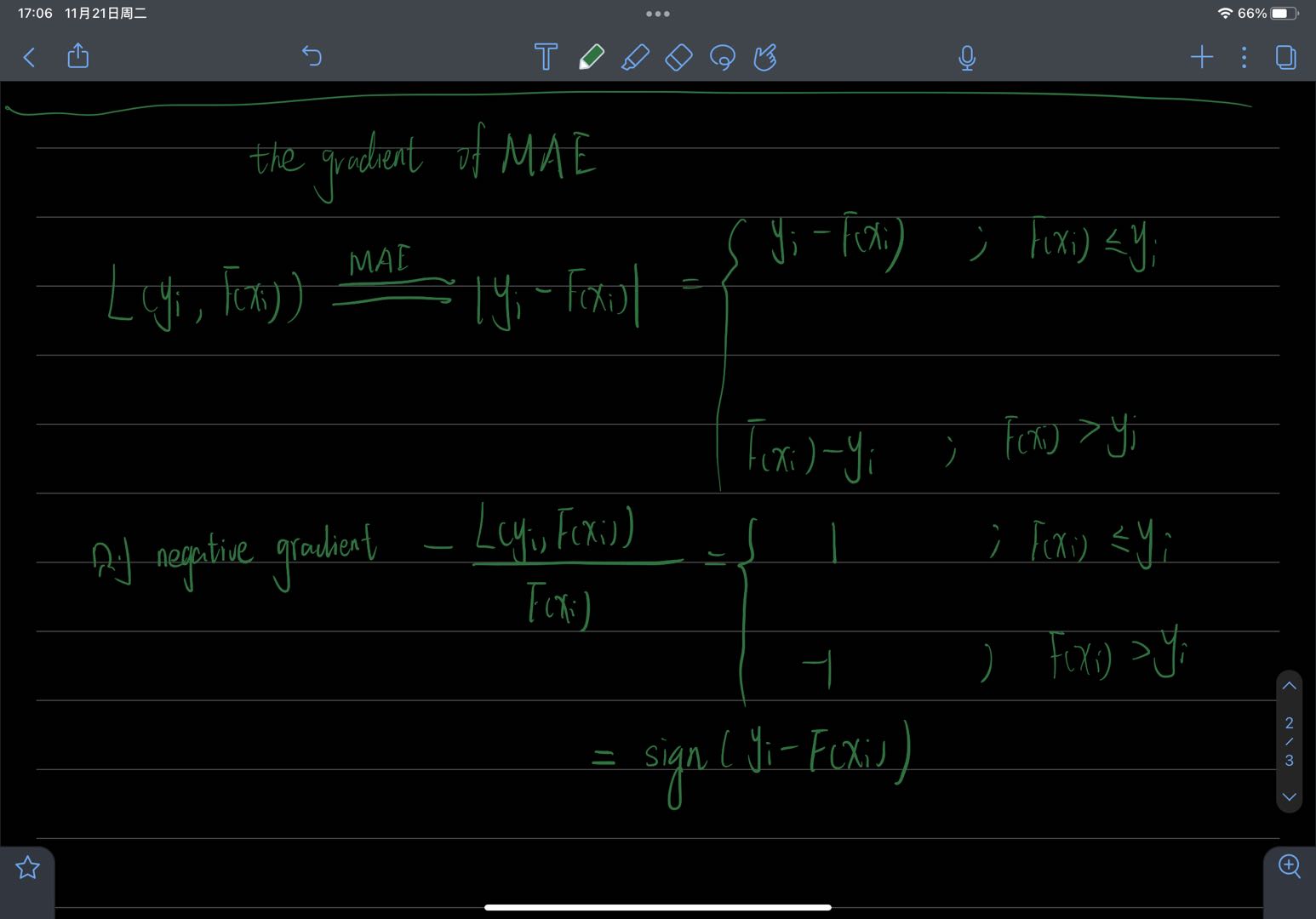
-
当损失函数次啊用logistic loss时(二分类任务) L ( y i , F ( x i ) ) = y i log ( p i ) + ( 1 − y i ) log ( 1 − p i ) \mathrm{L}\left(\mathrm{y}_{\mathrm{i}}, \mathrm{F}\left(\mathrm{x}_{\mathrm{i}}\right)\right)=\mathrm{y}_{\mathrm{i}} \log \left(\mathrm{p}_{\mathrm{i}}\right)+\left(1-\mathrm{y}_{\mathrm{i}}\right) \log \left(1-\mathrm{p}_{\mathrm{i}}\right) L(yi,F(xi))=yilog(pi)+(1−yi)log(1−pi)
则负梯度为
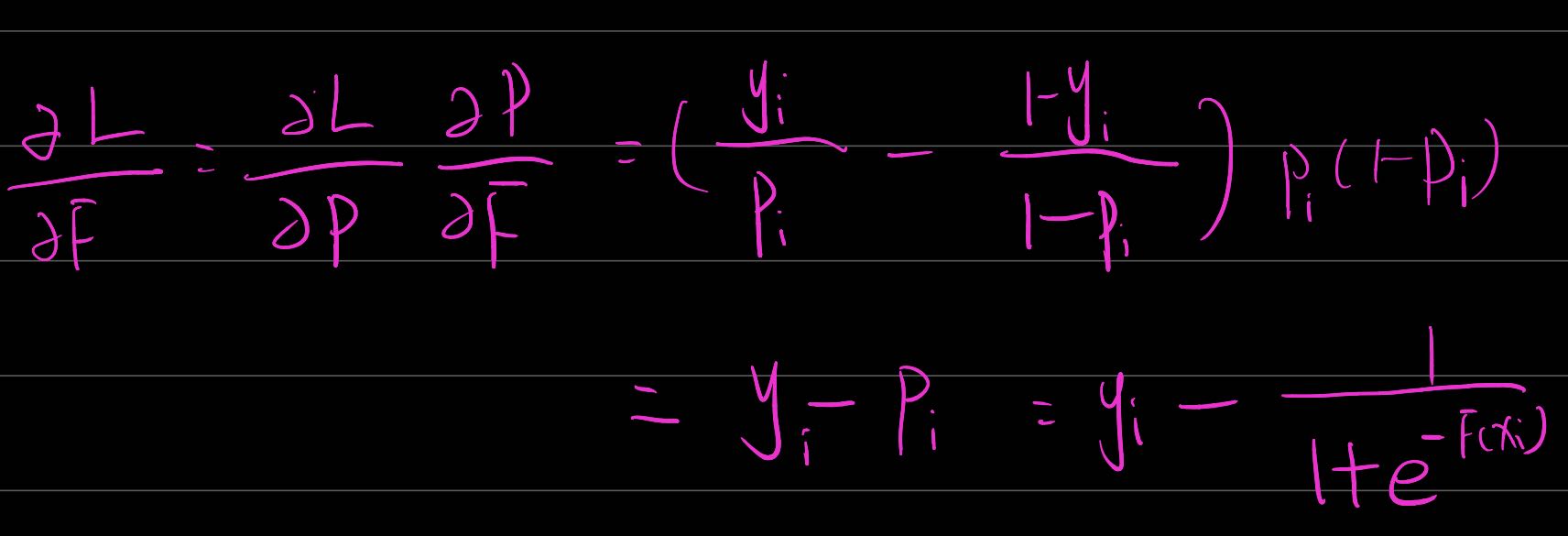

即:
-
损失函数 L ( x , y ) L(x,y) L(x,y) :用以衡量模型预测结果与真实结果的差异
-
弱评估器 f ( x ) f(x) f(x) :(一般为)决策树,不同的boosting算法使用不同的建树过程
-
综合集成结果 H ( x ) H(x) H(x):即集成算法具体如何输出集成结果
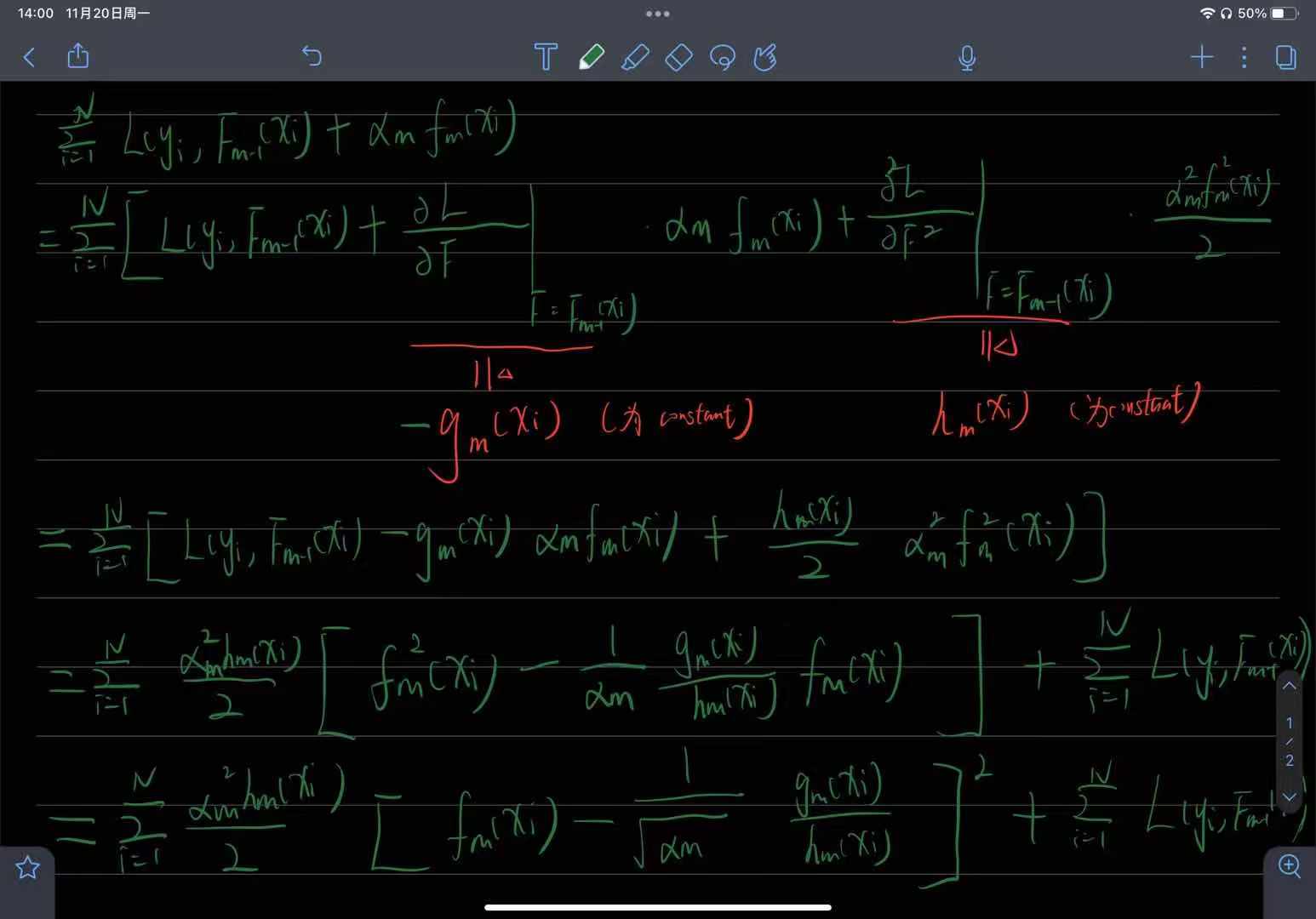
二阶泰勒展开
注:在分析 f m ( x i ) f_{m}(x_{i}) fm(xi)时可以将 α m \alpha_{m} αm视为常数,也是将 α m h m ( x i ) \sqrt{\alpha_{m}}h_{m}(x_{i}) αmhm(xi)合并成一个新的constant,同时将 α m 2 h m ( x i ) \alpha_{m}^{2}h_{m}(x_{i}) αm2hm(xi)也视为新的constant
回归树
采用树模型作为GBDT基学习器的优点是:
-
可解释性强;
-
可处理混合类型特征(既有连续型特征也有类别型特征) ;
-
具体伸缩不变性(不用归一化特征);
-
有特征组合的作用;
-
可自然地处理缺失值;
基于特征的划分: 决策树的构建是基于特征的划分的,每次选择一个特征来划分数据集。当在某个节点遇到缺失值时,树模型会考虑所有其他可用的特征进行划分。这种基于特征的划分使得树模型在训练和预测时能够灵活地处理缺失值。
不依赖线性关系: 决策树不依赖线性关系,而是通过树状结构递归地划分数据。对于每个节点,决策树都会选择最佳的划分方式,而当前节点的缺失值只会影响到当前节点的数据流向,并不会影响到其他节点的建立。(决策树能够根据数据的特征划分来构建决策树。这意味着,即使输入数据具有复杂的非线性关系,决策树也能够通过分层决策来模拟这种关系,从而实现对数据的分类。因为能处理分类变量和连续型变量,适合处理非线性的关系)
详细解释决策树可以处理非线性关系
- 分层划分: 决策树的核心思想是通过递归地选择最佳的特征和划分点,将数据集划分成不同的子集。每个划分代表了对输入空间的一个非线性划分。这种分层的划分方式使得决策树能够适应复杂的、非线性的数据结构。
- 多特征组合: 在决策树的每个节点上,模型可以同时考虑多个特征的组合**(x1<5且x7<8,特征中除了连续变量还有离散变量)**来进行划分。这允许决策树捕捉到输入特征之间的复杂交互关系,这些交互关系可以构成非线性关系。
- 递归特征选择: 决策树通过递归地选择最佳的特征和划分点,每次都在当前节点中选择对目标变量影响最大的特征**(适应数据的复杂结构)**。这种逐步的特征选择过程允许决策树在每个节点上根据目标变量的非线性关系进行选择,从而逐渐构建非线性模型。
- 不依赖线性关系: 决策树不对特征之间的关系做出线性假设**(由于决策树的贪心特征,使得不需要对特征之间进行多重共线性检验)**。每个节点的划分依赖于数据在当前节点上的分布,而不受到线性关系的限制。这使得决策树能够更灵活地适应各种非线性模式。
- 非参数化结构: 决策树是一种非参数化模型,不对数据的分布形式进行假设。这意味着决策树对于复杂的、非线性的数据结构没有先验假设,可以根据数据的实际情况进行拟合。
-
对异常点(异常值只占数据集的一小部分)鲁棒;(由于异常值的存在不太可能导致整个分割过程的变化,再基于多数投票原则,树模型在选择分割点时相对稳健。)
-
有特征选择作用;(基尼系数或者entropy)
-
可扩展性强;(可以处理不同规模的数据集;处理高维特征;处理非线性关系)
-
容易并行。(随机森林就是基于这个建立的)
缺点是:
1、 缺乏平滑性(回归预测时输出值只能输出有限的若干种数值,对于连续特征的划分一般是x<c, x>=c,对多棵树的输出结果【同一棵树对于新的样本每次判断结果都一样(叶子节点的均值),则最后这棵树的输出结果也是一样的】进行加权求和)
2、不适合处理高维稀疏数据(找到有效的分割点变得更加困难;当样本量相对于特征数较少时,树模型在高维稀疏数据上容易捕捉到噪声而不是信号)。
CART决策树(用于分类任务时,树的分裂准则采用基尼指数,用于回归任务时,用MSE、MAE和Friedman_mse【改进型的mse】)实际上是将空间用超平面进行划分的一种方法,每次分割的时候,都将当前的空间一分为二, 这样使得每一个叶子节点都是在空间中的一个不相交的区域,在进行决策的时候,会根据输入样本每一维feature的值,一步一步往下,最后使得样本落入N个区域中的一个(假设有N个叶子节点)。
回归树的参数主要有两个,一个叶子节点对应的区域(如何划分特征),另一个是叶子节点的取值(图中的The Height in each segment),其intuition就是使得划到特征空间每个区域的样本的方差足够小,足以用一个数值来代表,因此每个节点的分裂标准是划分到左右子树之后能不能是样本方差变小,即回归树使用方差衡量样本“纯度”(波动性),而分类树采用Gini系数或者熵来衡量样本纯不纯
回归树的例子如下图所示:


注意:timeline从左到右分别是2010/03/20,2011/03/01;my rate over love songs(对歌曲的喜爱程度)从下到上分别是0.2, 1.0, 1.2
回归树的表示方式: f ( x ; { b j , R j } ) = ∑ j = 1 J b j I ( x ∈ R j ) ( J 表示叶子节点个数 ) f(x;\left \{b_{j}, R_{j} \right \})=\sum_{j=1}^{J}b_jI(x \in R_{j})(J表示叶子节点个数) f(x;{bj,Rj})=∑j=1JbjI(x∈Rj)(J表示叶子节点个数)
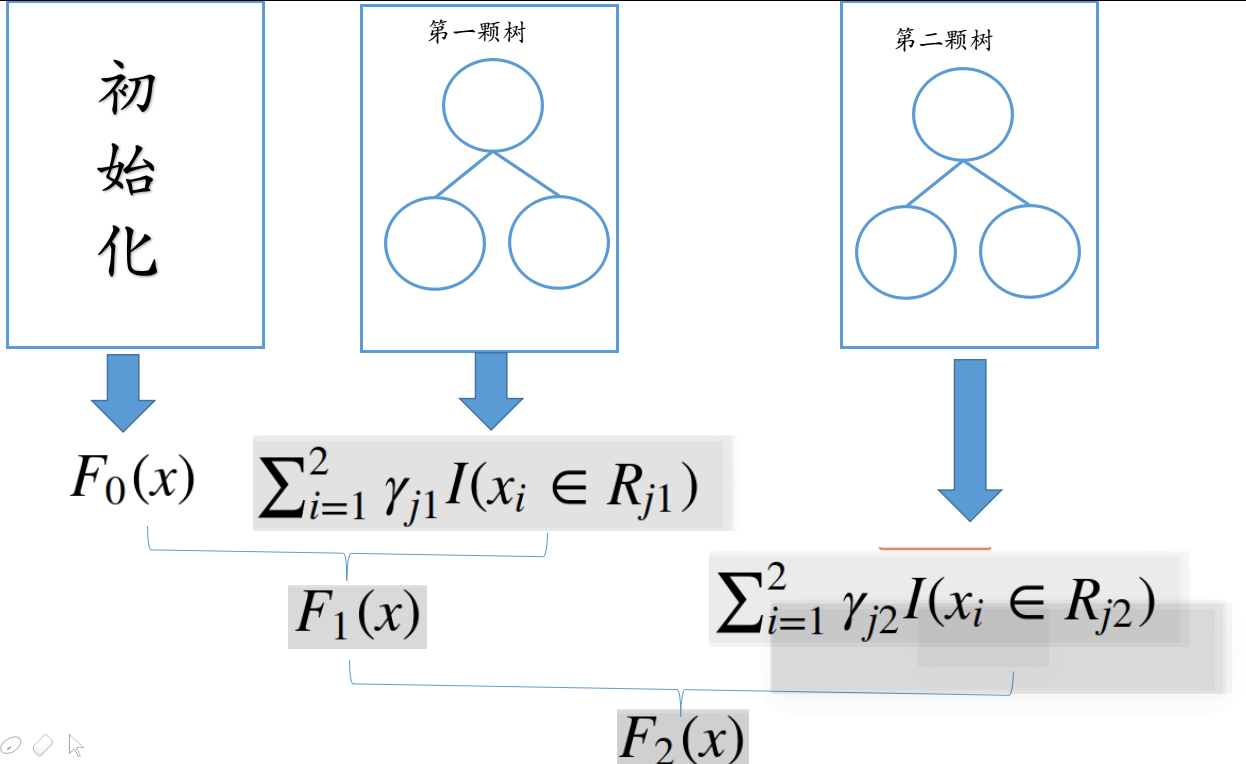
则对应于加法模型的GBDT的m轮迭代的结果是:
F m ( x ) = F m − 1 ( x ) + α m ∑ j = 1 J b j m I ( x ∈ R j m ) = ∑ k = 1 M T ( x ; θ k ) F_{m}(x)=F_{m-1}(x)+\alpha_{m} \sum_{j=1}^{J}b_{jm}I(x \in R_{jm})=\sum_{k=1}^MT(x;\theta_k) Fm(x)=Fm−1(x)+αm∑j=1JbjmI(x∈Rjm)=∑k=1MT(x;θk)
注意:加号后面的式子对应于上面的 f ( x ; { b j , R j } ) f(x;\left \{b_{j}, R_{j} \right \}) f(x;{bj,Rj}),因此可令 γ j m = α m b j m , 则 G B D T 的 m 轮迭代结果可以写成 \gamma_{jm}=\alpha_{m}b_{jm },则GBDT的m轮迭代结果可以写成 γjm=αmbjm,则GBDT的m轮迭代结果可以写成 F m ( x ) = F m − 1 ( x ) + ∑ j = 1 J γ j m I ( x ∈ R j m ) F_{m}(x)=F_{m-1}(x)+\sum_{j=1}^{J}\gamma_{jm}I(x \in R_{jm}) Fm(x)=Fm−1(x)+∑j=1JγjmI(x∈Rjm)(此时的参数只有一个: γ j m \gamma_{jm} γjm,原本只有两个参数: α m 和 b j m ( I ( x ∈ R j m 由 b j m 来决定 ) ) \alpha_{m}和b_{jm}(I(x\in R_{jm}由b_{jm}来决定)) αm和bjm(I(x∈Rjm由bjm来决定))
gbdt 无论用于分类还是回归一直都是使用的CART 回归树。这是因为gbdt 每轮的训练是在上一轮的训练的残差基础之上进行训练的。这里的残差就是当前模型的负梯度值 。这个要求每轮迭代的时候,弱分类器的输出的结果相减是有意义的。GBDT的核心就在于,每一棵树学的是之前所有树结论和的残差,这个残差就是一个加预测值后能得真实值的累加量。比如A的真实年龄是18岁,但第一棵树的预测年龄是12岁,差了6岁,即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习,如果第二棵树真的能把A分到6岁的叶子节点,那累加两棵树的结论就是A的真实年龄。
GBDT用于回归
- 对于回归问题,损失函数一般采用均方误差损失函数,即 C o s t = ∑ i = 1 N [ y i − F m − 1 ( x i ) − ∑ j = 1 J γ j m I ( x i ∈ R j m ) ] 2 Cost = \sum_{i=1}^N\left[y_i-F_{m-1}\left(x_i\right)-\sum_{j=1}^J \gamma_{jm} I\left(x_i \in R_{j m}\right)\right]^2 Cost=∑i=1N[yi−Fm−1(xi)−∑j=1JγjmI(xi∈Rjm)]2,因为 r m i = y i − F m − 1 ( x i ) r_{mi}=y_i - F_{m-1}(x_{i}) rmi=yi−Fm−1(xi),所以 C o s t = ∑ i = 1 N [ r m i − ∑ j = 1 J γ j m I ( x i ∈ R j m ) ] 2 ( 变量只有 γ j m ) Cost = \sum_{i=1}^N\left[r_{mi}-\sum_{j=1}^J \gamma_{jm} I\left(x_i \in R_{j m}\right)\right]^2(变量只有\gamma_{jm}) Cost=∑i=1N[rmi−∑j=1JγjmI(xi∈Rjm)]2(变量只有γjm),
γ j m = argmin γ m ∑ i = 1 N [ r m i − ∑ j = 1 J γ j m 1 ( x i ∈ R j m ) ] 2 , 其中 r m i = − ∂ L ( y i , F ( x ) ) ∂ F ( x ) ∣ F ( x ) = F m − 1 ( x i ) ,其中 L ( y i , F ( x ) ) = 1 2 ( y i − F ( x ) ) 2 \gamma_{jm} =\operatorname{argmin}_{\gamma_m} \sum_{i=1}^N\left[r_{mi}-\sum_{j=1}^J \gamma_{j m} 1\left(x_i \in R_{j m}\right)\right]^2,其中r_{mi}=-\frac{\partial L(y_{i}, F(x))}{\partial F(x)}|_{F(x)=F_{m-1}(x_{i})},其中L(y_{i}, F(x))=\frac{1}{2}(y_i - F(x))^2 γjm=argminγm∑i=1N[rmi−∑j=1Jγjm1(xi∈Rjm)]2,其中rmi=−∂F(x)∂L(yi,F(x))∣F(x)=Fm−1(xi),其中L(yi,F(x))=21(yi−F(x))2
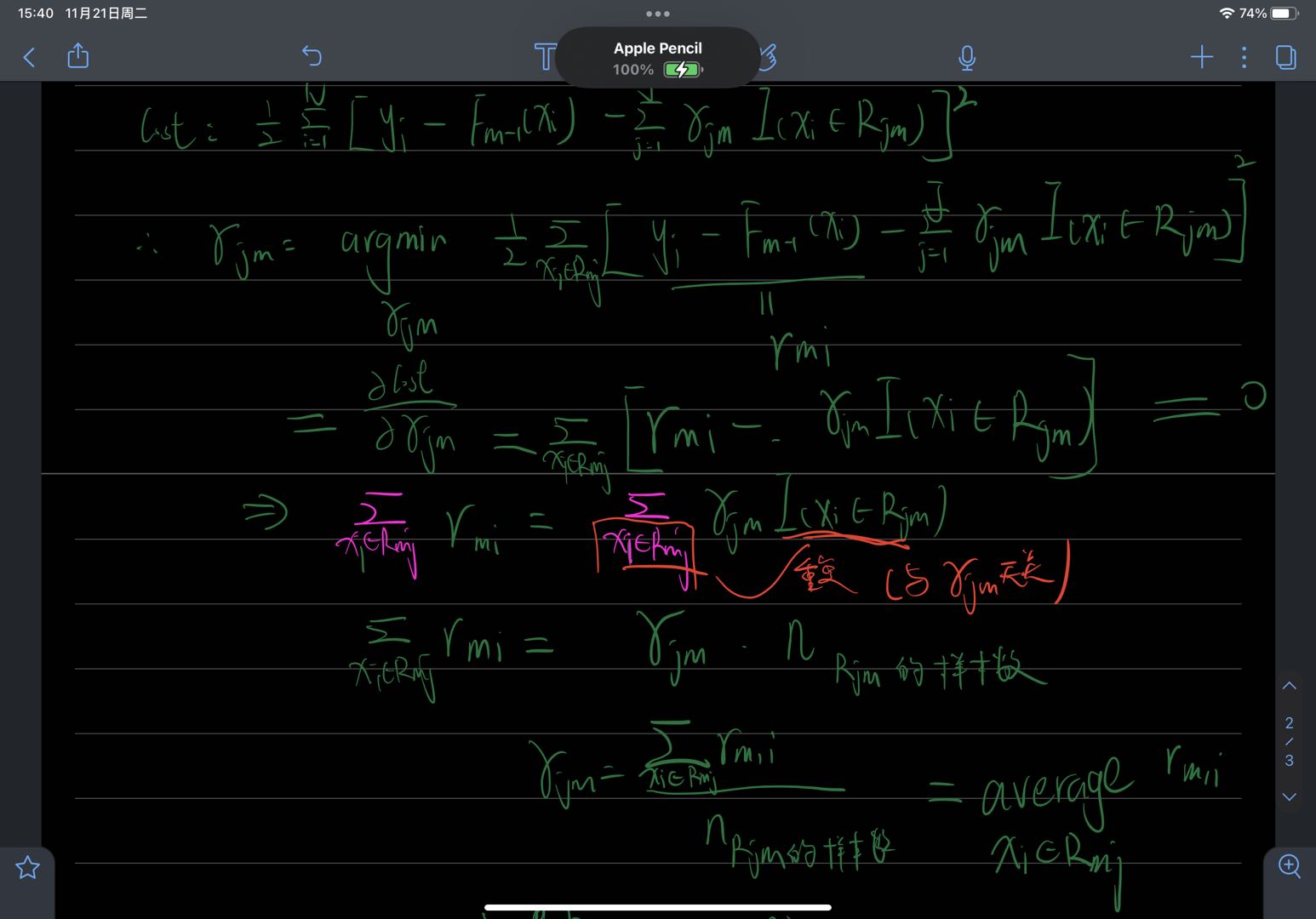
结论: γ j m = \gamma_{jm}= γjm= average x i ∈ R j m r m i _{x_i \in R_{j m}} r_{mi} xi∈Rjmrmi
例子
训练集:(A, 14岁)、(B,16岁)、(C, 24岁)、(D, 26岁);
训练数据的均值:20岁; (这个很重要,因为GBDT与i开始需要设置预测的均值,即第0个基学习器,这样后面才会有残差!)
决策树的个数:2棵;
开始GBDT学习了~
首先,输入初值20岁,根据第一个特征(具体选择哪些特征可以根据信息增益来计算选择),可以把4个样本分成两类,一类是购物金额<=1K,一类是>=1K的。假如这个时候我们就停止了第一棵树的学习,这时我们就可以统计一下每个叶子中包含哪些样本,这些样本的均值是多少,因为这个时候的均值就要作为所有被分到这个叶子的样本的预测值了。比如AB被分到左叶子,CD被分到右叶子,那么预测的结果就是:AB都是15岁,CD都是25岁。和他们的实际值一看,结果发现出现的残差,ABCD的残差分别是-1, 1, -1, 1。这个残差,我们要作为后面第二棵决策树的学习样本。
然后学习第二棵决策树,我们把第一棵的残差样本(A, -1岁)、(B,1岁)、(C, -1岁)、(D, 1岁)输入。此时我们选择的特征是经常去百度提问还是回答。这个时候我们又可以得到两部分,一部分是AC组成了左叶子,另一部分是BD组成的右叶子。那么,经过计算可知左叶子均值为-1,右叶子均值为1. 那么第二棵数的预测结果就是AC都是-1,BD都是1. 我们再来计算一下此时的残差,发现ABCD的残差都是0!停止学习~
这样,我们的两棵决策树就都学习好了。进入测试环节:
测试样本:请预测一个购物金额为3k,经常去百度问淘宝相关问题的女生的年龄~
我们提取2个特征:购物金额3k,经常去百度上面问问题;
第一棵树 —> 购物金额大于1k —> 右叶子,初步说明这个女生25岁
第二棵树 —> 经常去百度提问 —> 左叶子,说明这个女生的残差为-1;
叠加前面每棵树得到的结果:25-1=24岁,最终预测结果为24岁
- 当损失函数为MAE时,则 γ j m = m e d i a n x i ∈ R j m r m i \gamma_{j m}=median_{x_i \in R_{jm}}r_{mi} γjm=medianxi∈Rjmrmi 为梯度值。
例子:
| x i x_i xi | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| y i y_{i} yi | 5.56 | 5.7 | 5.91 | 6.4 | 6.8 | 7.05 | 8.9 | 8.7 | 9. | 9.05 |
前提:
- 选择MSE做为建树的分裂准则
- 选择MSE作为误差函数
- 树的深度设置为1
算法:
-
我们需要初始化 F 0 ( x ) F_0(x) F0(x),因此 F 0 ( x ) = 1 10 ∑ i = 1 10 r m i = 7.307 F_0(x)=\frac{1}{10}\sum_{i=1}^{10}r_{mi}=7.307 F0(x)=101∑i=110rmi=7.307;
-
拟合第一棵树,
r m i = − [ ∂ L ( y i , F ( x i ) ) ∂ F ( x i ) ] F ( x ) = F 0 ( x ) = ( y i − F 0 ( x i ) ) r_{mi}=-\left[\frac{\partial L(y_i,F(\mathbf{x}i))}{\partial F(\mathbf{x}i)}\right]_{F(x)=F_0(x)}=(y_i-F_0(x_i)) rmi=−[∂F(xi)∂L(yi,F(xi))]F(x)=F0(x)=(yi−F0(xi)),
用 { x i , r 0 i } 1 10 \left \{x_i, r_{0i} \right \}_1^{10} {xi,r0i}110来建树x i x_i xi 1 2 3 4 5 6 7 8 9 10 r 0 i r_{0i} r0i -1.747 -1.607 -1.397 -0.907 -0.507 -0.257 1.593 1.393 1.693 1.743 分析:
当选择 x i ≤ 1 和 x i > 1 作为分割点是, m e a n l e f t = − 1.747 , M S E l e f t = [ − 1.747 − ( − 1.737 ) ] 2 = 0 ; m e a n r i g h t = 1 9 ∑ i = 2 10 x i ≈ 0.19411 , M S E r i g h t = 1 9 ∑ i = 2 10 ( x i − m e a n ) 2 ≈ 1.747 ; 当选择x_i \le 1和x_i >1作为分割点是, mean_{left}=-1.747, MSE_{left}=[-1.747-(-1.737)]^2=0;\\mean_{right}=\frac{1}{9}\sum_{i=2}^{10}x_i\approx 0.19411,MSE_{right} = \frac{1}{9}\sum_{i=2}^{10}(x_i-mean)^2\approx1.747; 当选择xi≤1和xi>1作为分割点是,meanleft=−1.747,MSEleft=[−1.747−(−1.737)]2=0;meanright=91∑i=210xi≈0.19411,MSEright=91∑i=210(xi−mean)2≈1.747;
当选择 x i ≤ 2 和 x i > 2 作为分割点是, m e a n l e f t = 1 2 ∑ i = 1 2 x i = − 1.677 , M S E l e f t = 1 2 ∑ i = 1 2 ( x i − m e a n l e f t ) 2 = 0.419 ; m e a n r i g h t = 1 8 ∑ i = 3 10 x i ≈ 0.19411 , M S E r i g h t = 1 8 ∑ i = 2 10 ( x i − m e a n ) 2 ≈ 1.509 ; 当选择x_i \le 2和x_i >2作为分割点是, mean_{left}=\frac{1}{2}\sum_{i=1}^{2}x_i=-1.677, MSE_{left}=\frac{1}{2}\sum_{i=1}^{2}(x_i-mean_{left})^2=0.419;\\mean_{right}=\frac{1}{8}\sum_{i=3}^{10}x_i\approx 0.19411,MSE_{right} = \frac{1}{8}\sum_{i=2}^{10}(x_i-mean)^2\approx1.509; 当选择xi≤2和xi>2作为分割点是,meanleft=21∑i=12xi=−1.677,MSEleft=21∑i=12(xi−meanleft)2=0.419;meanright=81∑i=310xi≈0.19411,MSEright=81∑i=210(xi−mean)2≈1.509;
依次,穷尽所有取值。
可以得到当选择6 66作为分裂点时 M S E s u m = 0.3276 MSE_{sum}=0.3276 MSEsum=0.3276最小。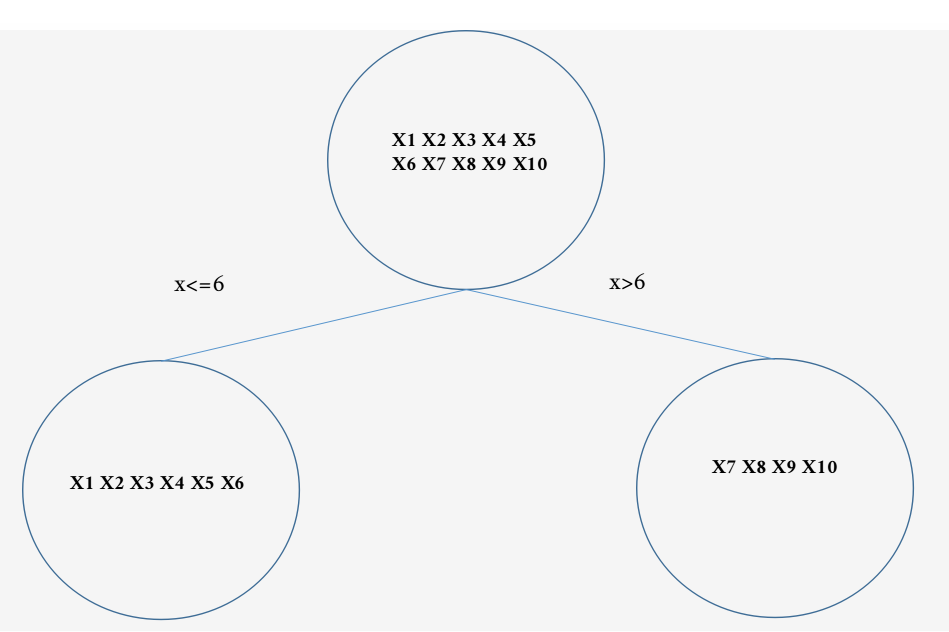
至此,我们完成了第一颗树的拟合,拟合完之后我们得到了 R j m R_{jm} Rjm以及 γ j m \gamma{jm} γjm:
-
R 11 : x i ≤ 6 ; R 21 : x i > 6 R_{11}:x_i \le 6;R_{21}:x_{i}> 6 R11:xi≤6;R21:xi>6
-
γ 11 = r 01 + r 02 + r 03 + r 04 + r 05 + r 06 6 = − 1.0703 γ 21 = r 07 + r 08 + r 09 + r 0 , 10 4 = 1.6055 \begin{aligned} & \gamma_{11}=\frac{r_{01}+r_{02}+r_{03}+r_{04}+r_{05}+r_{06}}{6}=-1.0703 \\ & \gamma_{21}=\frac{r_{07}+r_{08}+r_{09}+r_{0,10}}{4}=1.6055 \end{aligned} γ11=6r01+r02+r03+r04+r05+r06=−1.0703γ21=4r07+r08+r09+r0,10=1.6055
最后更新 F 1 ( x i ) \mathrm{F}_1\left(\mathrm{x}_{\mathrm{i}}\right) F1(xi) 值, F 1 ( x i ) = F 0 ( x i ) + ∑ j = 1 2 γ j 1 I ( x i ∈ R j 1 ) \mathrm{F}_1\left(\mathrm{x}_{\mathrm{i}}\right)=\mathrm{F}_0\left(\mathrm{x}_{\mathrm{i}}\right)+\sum_{\mathrm{j}=1}^2 \gamma_{\mathrm{j} 1} \mathrm{I}\left(\mathrm{x}_{\mathrm{i}} \in \mathrm{R}_{\mathrm{j} 1}\right) F1(xi)=F0(xi)+∑j=12γj1I(xi∈Rj1) 。
比如更新其中一个样本 x 1 x_1 x1 的值:
F 1 ( x 1 ) = F 0 ( x 1 ) + η ∗ ∑ j = 1 2 γ j 1 I ( x 1 ∈ R j 1 ) = 7.307 − 0.1 ∗ 1.0703 = 7.19997 ( η 表示 l e a r n i n g r a t e = 0.1 ) \mathrm{F}_1\left(\mathrm{x}_1\right)=\mathrm{F}_0\left(\mathrm{x}_1\right)+\eta * \sum_{\mathrm{j}=1}^2 \gamma_{\mathrm{j} 1} \mathrm{I}\left(\mathrm{x}_1 \in \mathrm{R}_{\mathrm{j} 1}\right)\\ =7.307-0.1 * 1.0703=7.19997 (\eta表示learning\ rate=0.1) F1(x1)=F0(x1)+η∗j=1∑2γj1I(x1∈Rj1)=7.307−0.1∗1.0703=7.19997(η表示learning rate=0.1)
-
-
拟合第二颗树(m = 2)
$ \gamma_{11}=-\left[\frac{\partial L(y_i,F(\mathbf{x}i))}{\partial F(\mathbf{x}i)}\right]{{F(x)=F{m-1}(x)}}=(y_1-F_{1}(x_1))=(5.56-7.19997)=-1.63997$
| x i x_i xi | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| r 1 i r_{1i} r1i | -1.63997 | -1.49997 | -1.28997 | -0.79997 | -0.39997 | -0.14997 | 1.43245 | 1.23245 | 1.53245 | 1.58245 |
得到两个叶子节点的值: γ 12 = − 0.9633 , γ 22 = 1.44495 \gamma_{12}=−0.9633, \gamma_{22}=1.44495 γ12=−0.9633,γ22=1.44495
伪代码

注意:重点关注2-c,可以理解为训练集训练完决策树模型叶子节点的均值(每一棵树只有一个输出值,根据测试样本进入决策树过后判定的递归顺序得到的结果)





























 536
536











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








