折射率测量方案-科学指南针

01

方案概述

根据折射定律，当两介质折射率不同时，光线从一介质进入另一介质时，光线将发生偏折，入射角和折射角不相等。而我们可以将角度的变化转化为光斑位移的变化。因此，可以利用光电位置敏感器件测量光斑位移的变化量，从而计算出待测介质的折射率。

02

测量原理及公式

图1

如图1，我们需要找出光斑位移量与折射率之间的关系，因此我们建立关系式：

由上式有

再利用折射定律与三角变化公式有

最终将公式中的提取出来可得

根据上式，我们可以得出，只需要将已知厚度的待测平行平板介质放置在固定的角度上，然后测量出光斑的位移量我们即可以求出折射率。因此，我们测量光路图可按如下方式放置：

图2

图2中滤光片的作用是为了得到单色光，避免PSD对不同波段的响应特性不同造成误差；狭缝是为了产生较细的条纹，为了PSD能更好地测量。待测介质则需要是平行平板，以一定的角度放置在码盘上，确定入射角度。

图3

其中PSD的原理是当入射光斑照射在光敏面上能产生与光强成比例的光电流。而且由于 P 层的电阻是均匀的 ,所以由两极输出的电流分别与光点到两极的距离成反比。

光斑位移量与电流之间的关系有

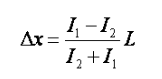
因此我们只需测量两极电流即可得到光斑的位移变化量，从而即能计算出待测介质的折射率。

03

误差分析

3.1量程的探究

以常见的K9冕牌玻璃为例进行分析，其折射率，假设平行平板玻璃厚度为5cm，光线以的入射角入射，则产生的位移量

(3-1)

(3-2)

根据滨松官方资料得知，一般一维PSD的探测面在2mm-40mm之间，可以满足折射率的测量，且可以通过调整平行平板的厚度调节位移的偏移量，控制在量程之内。

本次误差分析以一款常见的一维PSD产品为例，型号：PSD-1315，其有效感应面积达到，分辨率为0.1um，在5mm厚的平行平板的条件下即可测量折射率的介质，可以实现高折射率的测量。

3.2折射率的标准不确定度

折射率的测量误差主要来源于三个方面：

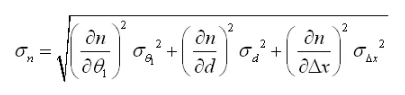
(3-3)

其中

(3-4)

(3-6)

(3-7)

其中当厚度d可以采用螺旋测微仪测量，入射角用角度盘确定时，厚度测量的标准不确定度和入射角测量的标准不确定度均为

(3-8)

式中

螺旋测微仪的精度可达到10um，而码盘精度较高的有一、二等三角测量的J07级仪器，水平度盘格值可达到1'。

其中的测量的误差主要来源有狭缝的衍射因素和PSD的分辨力，但如果衍射的光束能量分布稳定，由于我们测量的是位移的相对变化量，因此可以排除衍射造成的影响。最终的测量的误差将由PSD的分辨率决定。

(3-9)

通过计算

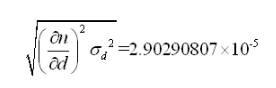
(3-10)

(3-11)

(3-12)

(3-13)

综上分析，最终通过选用上述的器材进行测量时,产生的误差可以达到0.045，而且由和d产生的误差相对于度盘都可以忽略不计，因此若想进一步提高测量精度，主要考虑提高入射角的精度，且通过计算，若入射角的误差减少到光学度盘的5”~10”时,误差可以减少到10-4。

更多科研干货教程，可以点击下面链接获取哦~

折射率