R之线性回归模型
一、简单线性回归
“回归”一词首先由英国生物统计学家S.F.Galton(1885)提出,他发现高个子父代的子代平均身高不是更高,而是稍矮;相反,矮个子父代的子代平均身高并不是更矮,而是稍高于其父代水平。他把这种身高趋向种族稳定的现象称为“回归”。目前回归的含义已经演变成变量之间某种数量依存关系。
**直线回归分析:**分析两个变量间的数量关系,目的是用一个变量推算另一个变量(建立回归方程)。
直线相关分析:分析两个变量之间有无相关关系以及相关的性质(正、负相关)和相关的密切程度。
比如:弟弟身高与哥哥身高的关系?儿子身高与父亲身高的关系?
再比如:年龄(X)与尿肌酐含量(Y)研究;身高(X)与体重(Y)研究
1、回归分析对于资料的要求
回归分析涉及到两个变量, X与Y,其中X称自变量, Y 为因变量或反应变量
Y:必须是呈正态分布的随机变量
X:不一定
- 可以是非随机变量:年龄、药物浓度或剂量 — Ⅰ 型回归
- 可以是随机变量:身高、体重、血清胆固醇的含量,血红蛋白的含量 — Ⅱ型回归
2、直线回归方程
由X推算Y的直线回归方程一般表达式:

a称为截距, b 为回归系数, 即直线的斜率
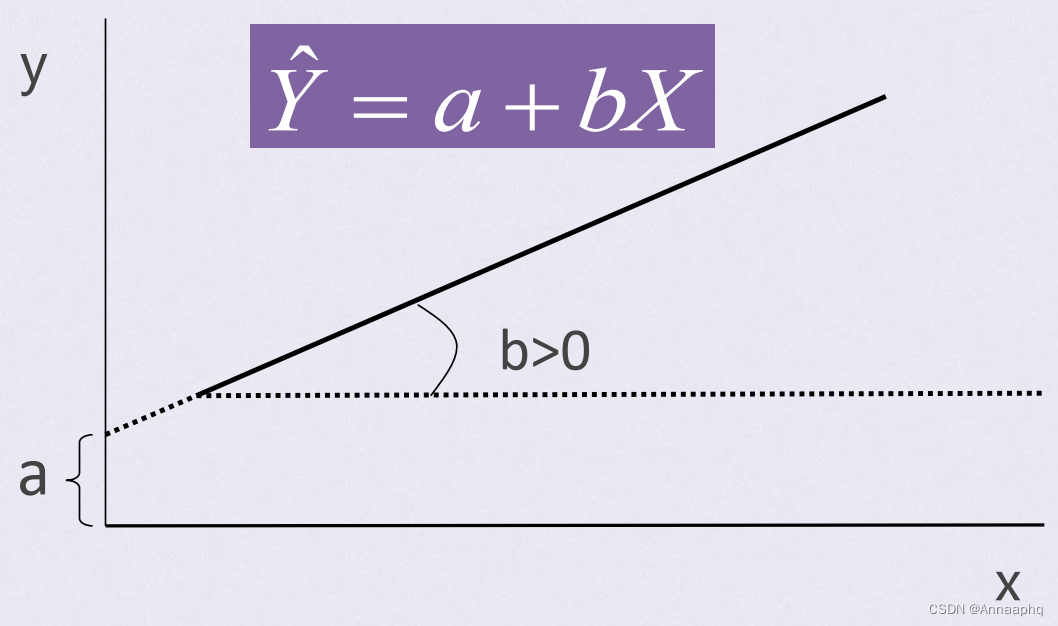
3、直线回归方程的建立



回归系数b的统计学意义:
- b>0时,Y随X增大而增大;
- b<0时,Y随X的增大而减少;
- b=0时,X与Y无直线关系。
- b的统计学意义是: X每增(减)一个单位, Y平均改变b个单位。
4、回归分析步骤
- 用原始数据绘制散点图;
- 求a和b (如果呈直线关系)
- 对回归系数b作假设检验(方法: a. F检验 b. t检验 c. 用r检验来代替)。
- 如果x与y存在直线关系( b假设检验的结果P<0.05),列出回归方程。否
则,不列回归方程。
5、回归系数b的假设检验
所建立的回归方程,不一定都有意义,必须对回归方程和回归系数进行假设检验。直线回归方程一般只对回归系数进行假设检验
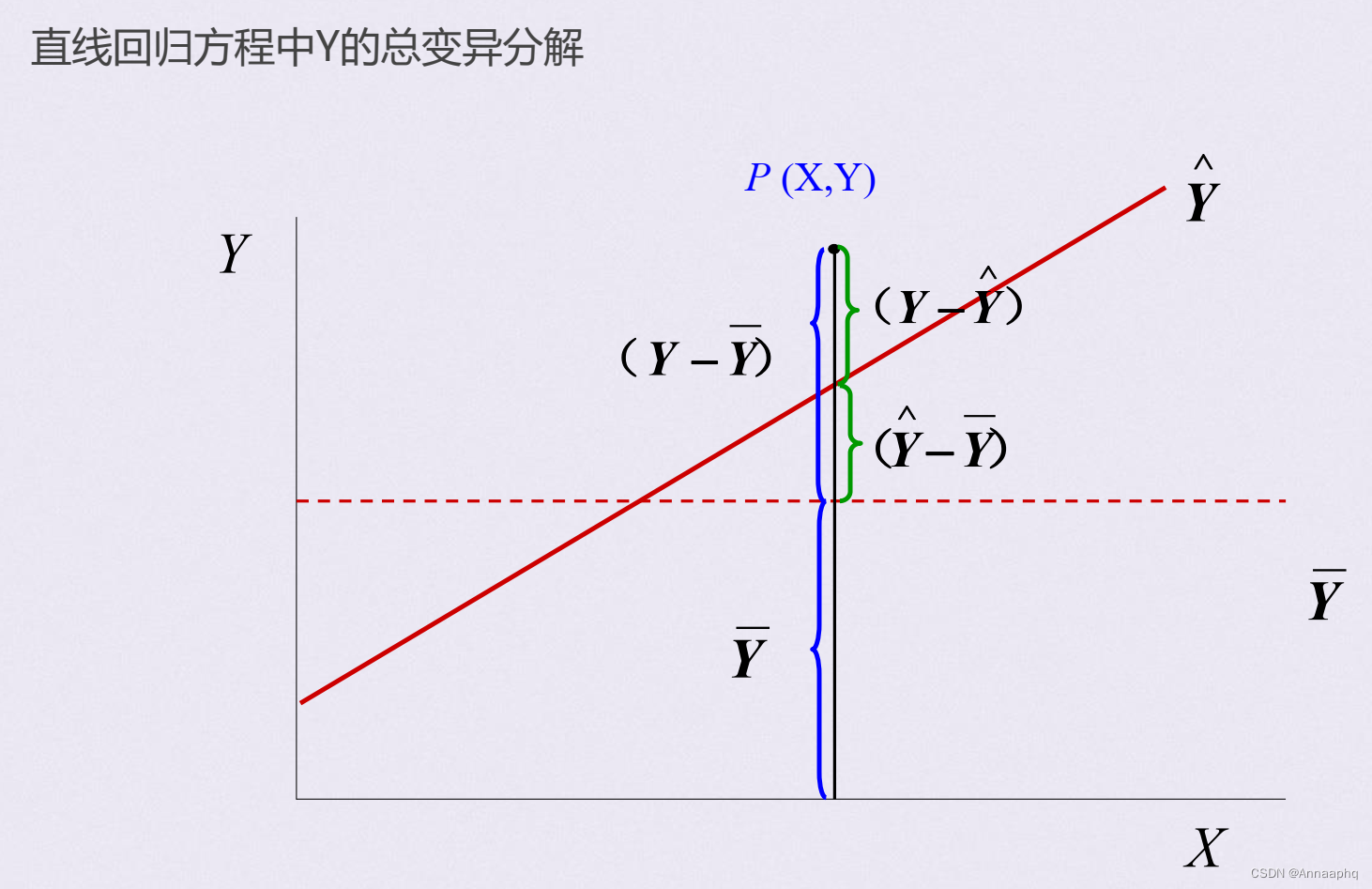
Y的离均差平方和的划分:
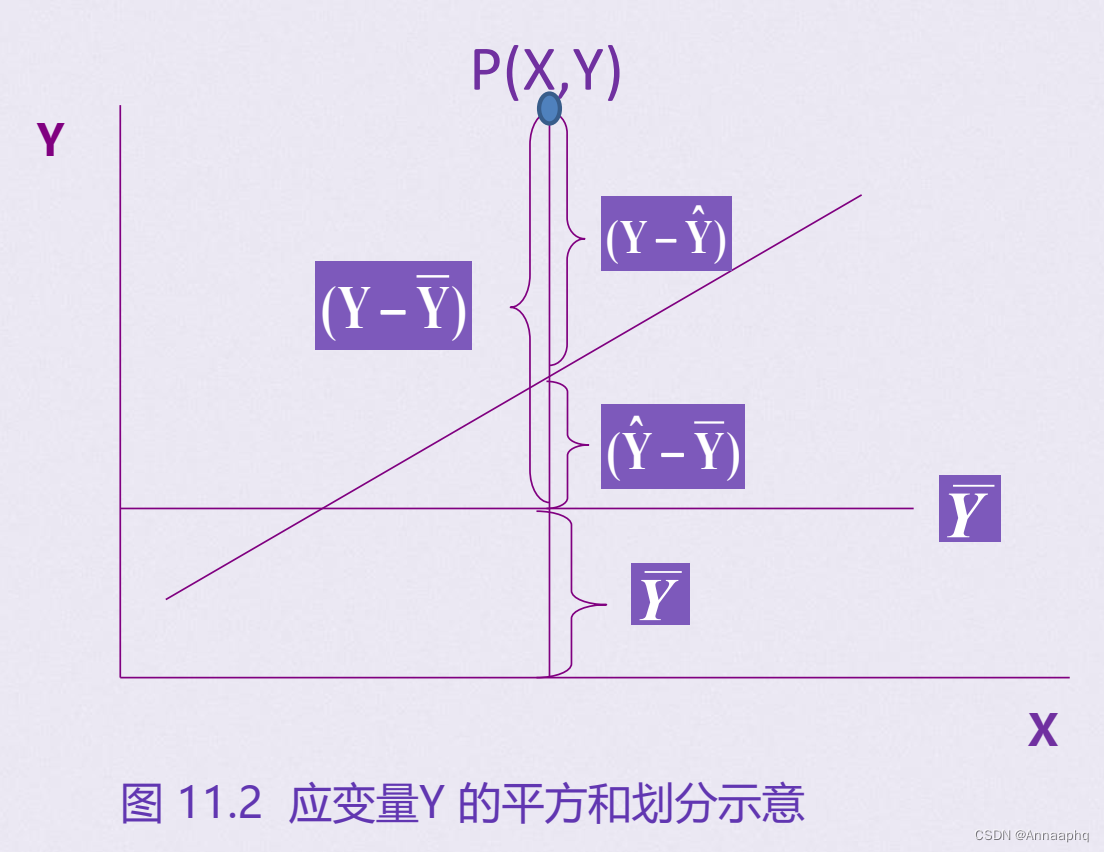
Y的平方和所划分的三段的含义:

三种平方和的关系:


三种平方和的意义:
- SS总, 为Y值的离均差平方和, 说明未考虑X与Y的回归关系时Y总的变异。
- SS回, 它反映在Y的变异中由于X与Y的直线关系而使Y变异减少的部分, 也是在总平方和中可以用X解析的部分。 SS回越大, 说明回归效果越好。
- SS剩, 反映X对Y的线性影响之外其它因素对Y的变异的作用, 也是在总平方和中无法用X解析的部分。 SS剩越小, 说明回归方程的估计误差越小。
5.1 b的假设检验方法1——方差分析法

5.2 b的假设检验方法2——t检验法
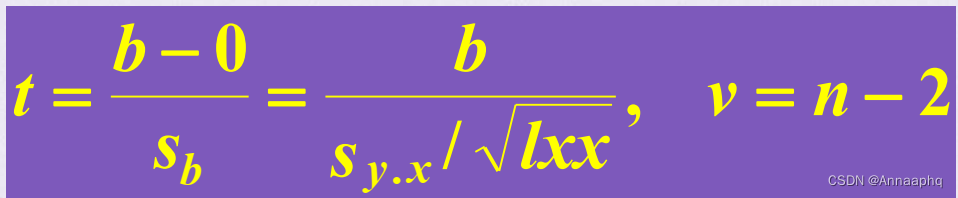

6、总体回归系数β区间的估计

7、应用直线回归分析应注意的问题
- 作回归分析要有实际意义
- 进行直线回归分析前,应绘制散点图,一方面看散点是否呈直线趋势,另一方面观察有无异常点、高杠杆点和强影响点
- 注意建立线性回归模型的基本条件:线性、独立性、正态性、方差齐性
- 直线回归方程的适用范围以求回归方程时X的实测值范围为限;若无充分理由证明超过该范围还是直线,应避免外延。
- 两变量有线性关系,不一定是因果关系,也不一定表明两变量间确有内在联系。
8、用lm()拟合线性回归模型
在R中,拟合线性模型最基本的函数就是lm(),格式为:
myfit <- lm(formula, data)
其中, formula指要拟合的模型形式, data是一个数据框,包含了用于拟合模型的数据。结果对象(本例中是myfit)存储在一个列表中,包含了所拟合模型的大量信息。
表达式(formula)形式如下:
Y ~ X1 + X2 + ... + Xk
~左边为响应变量,右边为各个预测变量,预测变量之间用+符号分隔。表8-2中的符号可以用不同方式修改这一表达式 :

对拟合线性模型非常有用的其他函数
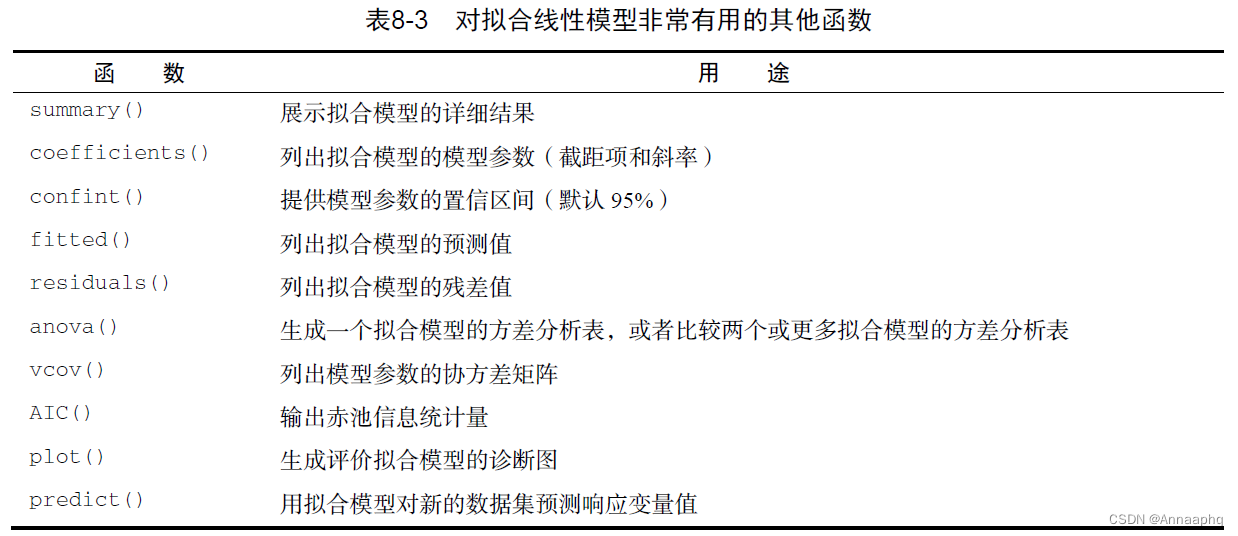
当回归模型包含一个因变量和一个自变量时,我们称为简单线性回归。当只有一个预测变量,但同时包含变量的幂(比如, X、 X^2、 X^3)时,我们称为多项式回归。当有不止一个预测变量时,则称为多元线性回归。
9、案例1
让我们通过一个回归示例来熟悉表8-3中的函数。基础安装中的数据集women提供了15个年龄在30~39岁间女性的身高和体重信息,我们想通过身高来预测体重,获得一个等式可以帮助我们分辨出那些过重或过轻的个体
fit <- lm(weight ~ height, data=women)
summary(fit)
women$weight
fitted(fit)
residuals(fit)
plot(women$height,women$weight,
main="Women Age 30-39",
xlab="Height (in inches)",
ylab="Weight (in pounds)")
# add the line of best fit
abline(fit)
查看与身高平方的关系:
fit2 <- lm(weight ~ height + I(height^2), data=women)
summary(fit2)
plot(women$height,women$weight,
main="Women Age 30-39",
xlab="Height (in inches)",
ylab="Weight (in lbs)")
lines(women$height,fitted(fit2))
查看与身高三次方的关系:
fit3 <- lm(weight ~ height + I(height^2) +I(height^3), data=women)
summary(fit3)
plot(women$height,women$weight,
main="Women Age 30-39",
xlab="Height (in inches)",
ylab="Weight (in lbs)")
lines(women$height,fitted(fit3))
画一个散点图:
library(car)
scatterplot(weight ~ height, data=women,
spread=FALSE, smoother.args=list(lty=2), pch=19,
main="Women Age 30-39",
xlab="Height (inches)",
ylab="Weight (lbs.)")
回归的结果也可以作图:
fit <- lm(weight ~ height, data=women)
par(mfrow=c(2,2))
plot(fit)
newfit <- lm(weight ~ height + I(height^2), data=women)
par(opar)
par(mfrow=c(2,2))
plot(newfit)
par(opar)
10、案例2
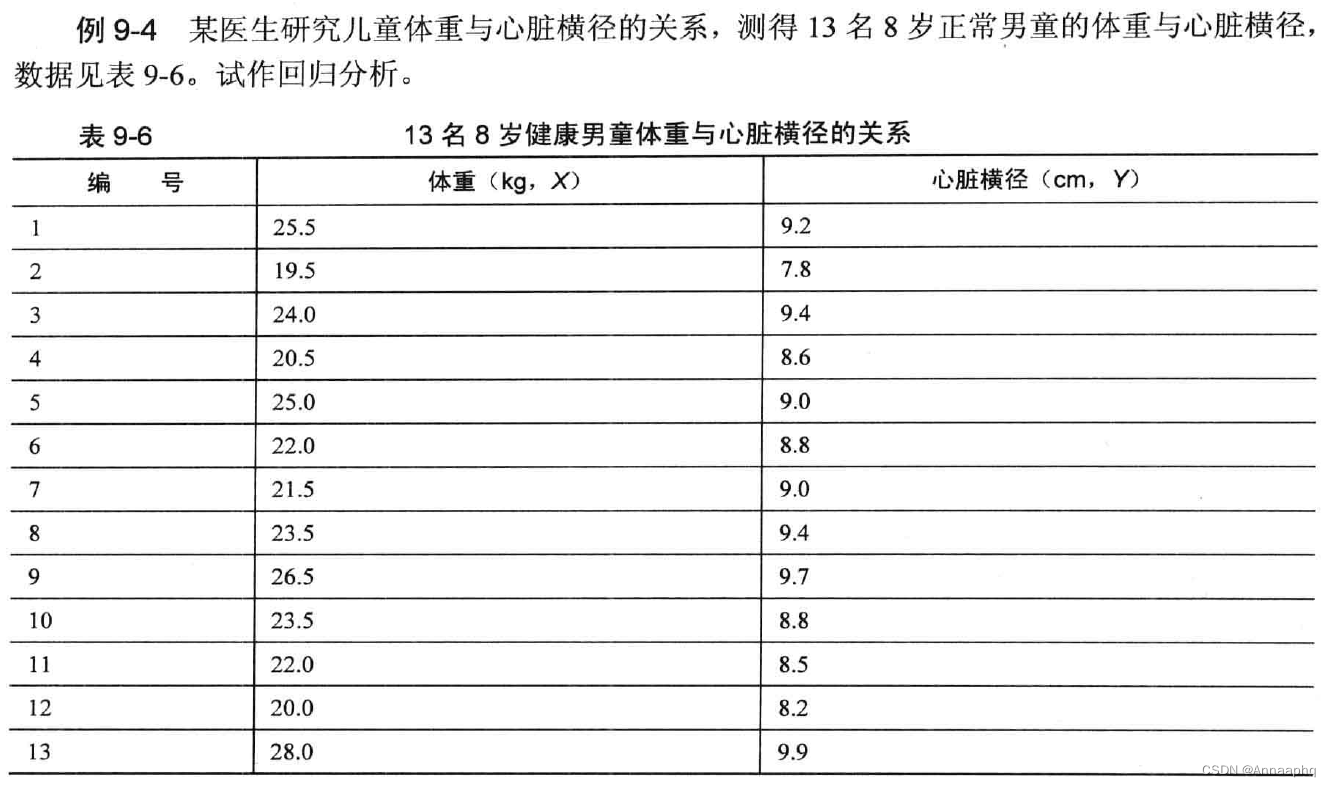
Example9_4 <- read.table ("example9_4.csv", header=TRUE, sep=",")
attach(Example9_4)
plot(x, y)
fit <-lm(y~x)
anova(fit)
summary (fit)
confint(fit)
y
fitted (fit)
residuals (fit)
detach (Example9_4)
11、案例3
大多数公司最终会询问关于花费在广告上的费用对公司产品销售额的影响程度。由于广告需要一定的时间才能达到它的效应,同时它的效应也不是永久持续的,它的影响也许仅仅延续开头的一段时期。假设公司相信销售额与当月以及前两个月内所花的广告费有较密切的关系,假设它们之间存在线性关系,现在有某公司15 月内有关广告花费X 与销售额Y 的数据,如下表所示
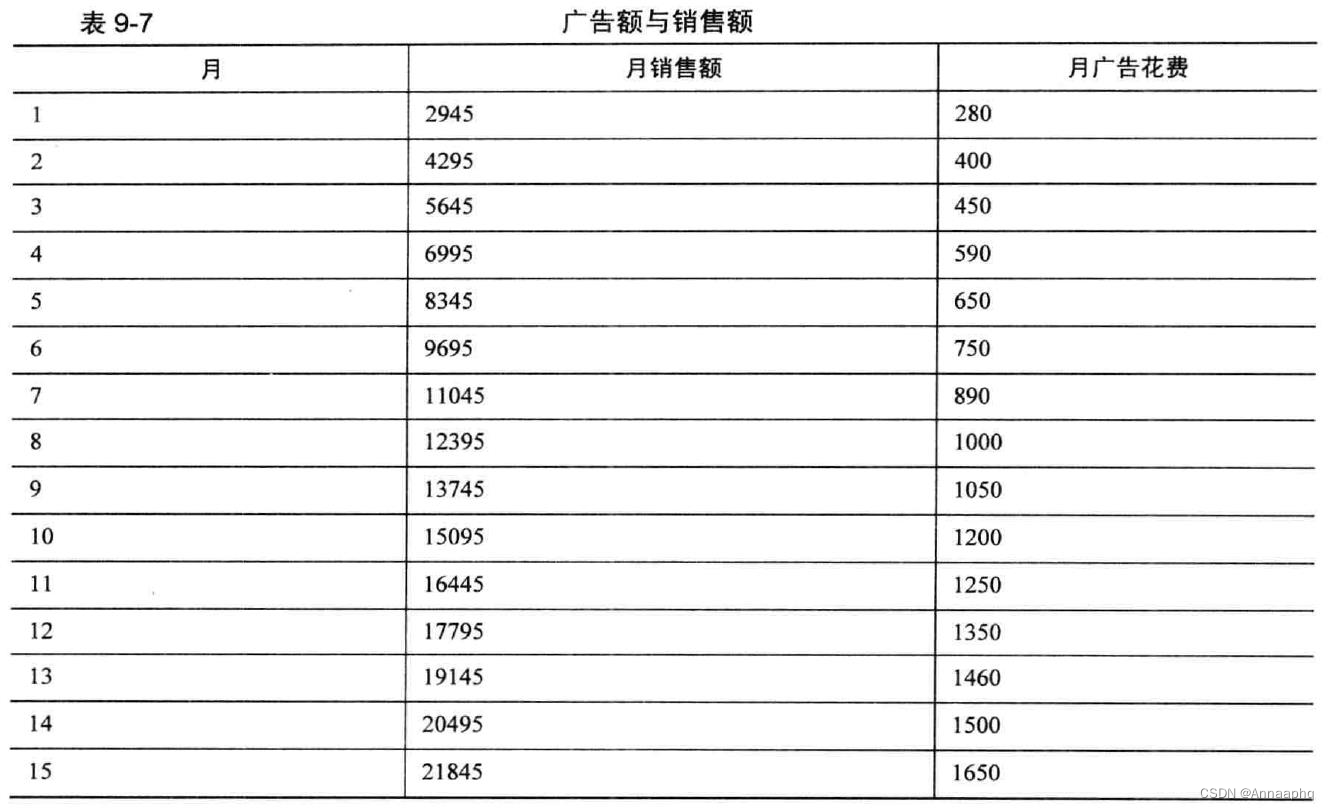
Example9_5 <- read.table ("example9_5.csv", header=TRUE, sep=",")
attach(Example9_5)
fit <- lm(SALES~ADV + ADVLAG1 + ADVLAG2,data=Example9_5)
anova(fit)
summary (fit)
SALES
fitted (fit)
residuals (fit)
detach (Example9_5)
备注:ADV指当月广告费,ADVLAG1指上上个月广告费,ADVLAG2指上个月广告费
二、残差与回归值&预测域与置信带

library(ISwR)
> attach(thuesen)
> lm.velo <- lm(short.velocity~blood.glucose)
> fitted(lm.velo)
> plot(blood.glucose,short.velocity)
# lines(blood.glucose,fitted(lm.velo)) # wrong 因有缺失值,所以此命令报错
> lines(blood.glucose[!is.na(short.velocity)],fitted(lm.velo))
#缺失值也可以这样处理
cc <- complete.cases(thuesen)
options(na.action=na.exclude)
lm.velo <- lm(short.velocity~blood.glucose)
fitted(lm.velo)
lines(blood.glucose,fitted(lm.velo))
#segment画线段
> segments(blood.glucose,fitted(lm.velo),
blood.glucose,short.velocity) # 带有残差线段的图形
> plot(fitted(lm.velo),resid(lm.velo)) # 残差与回归值的散点图
> qqnorm(resid(lm.velo)) # Q-Q图,符合条件,残差符合正态性
画带有置信区间的散点图:
predict(lm.velo)
> predict(lm.velo,int="c") # 置信区间confidence interval.
> predict(lm.velo,int="p") # 预测区间prediction interval. 预测区间PI总是要比对应的置
信区间CI大,这是因为在对单个响应与响应均值的预测中包括了更多的不确定性。
> # pred.frame <- data.frame(thuesen[4:20,]) # blood.glucose 的值是随机排列的,我
们不希望置信曲线上的线段杂乱无章地排列,可对数据进行简化与筛选,如下:
> pred.frame <- data.frame(blood.glucose = 4:20) #只选4-20行
> pp <- predict(lm.velo, int="p", newdata=pred.frame)
> pc <- predict(lm.velo, int="c", newdata=pred.frame)
> plot(blood.glucose, short.velocity,ylim=range(short.velocity, pp, na.rm=T))
#na.rm=T去除缺失值,y轴刻度范围,包含最大值与最小值
> pred.gluc <- pred.frame$blood.glucose
> matlines(pred.gluc, pc, lty=c(1,2,2), col="black")
> matlines(pred.gluc, pp, lty=c(1,3,3), col="black")
> detach(thuesen)
三、多元线性回归模型

1、回归模型的应用条件

2、偏回归系数的估计
最小二乘法
基本思想:使残差平方和最小
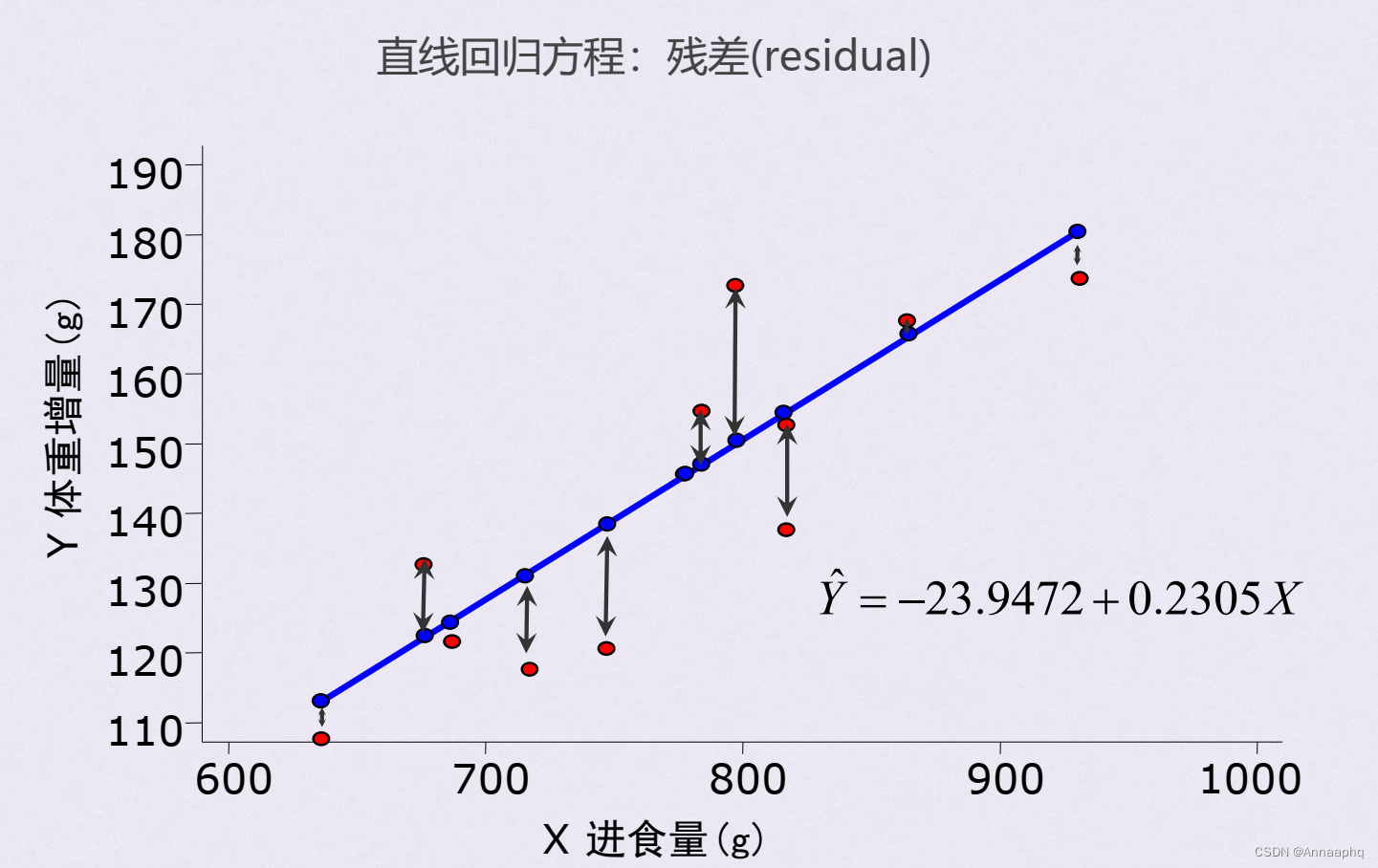
3、回归方差的假设检验

4、案例1
某学校20 名一年级女大学生体重(公斤〉 、胸围(厘米)、肩宽( 厘米)及肺活量( 升〉 实测值如表1 0-1 所示,试对影响女大学生肺活量的有关因素作多元回归分析
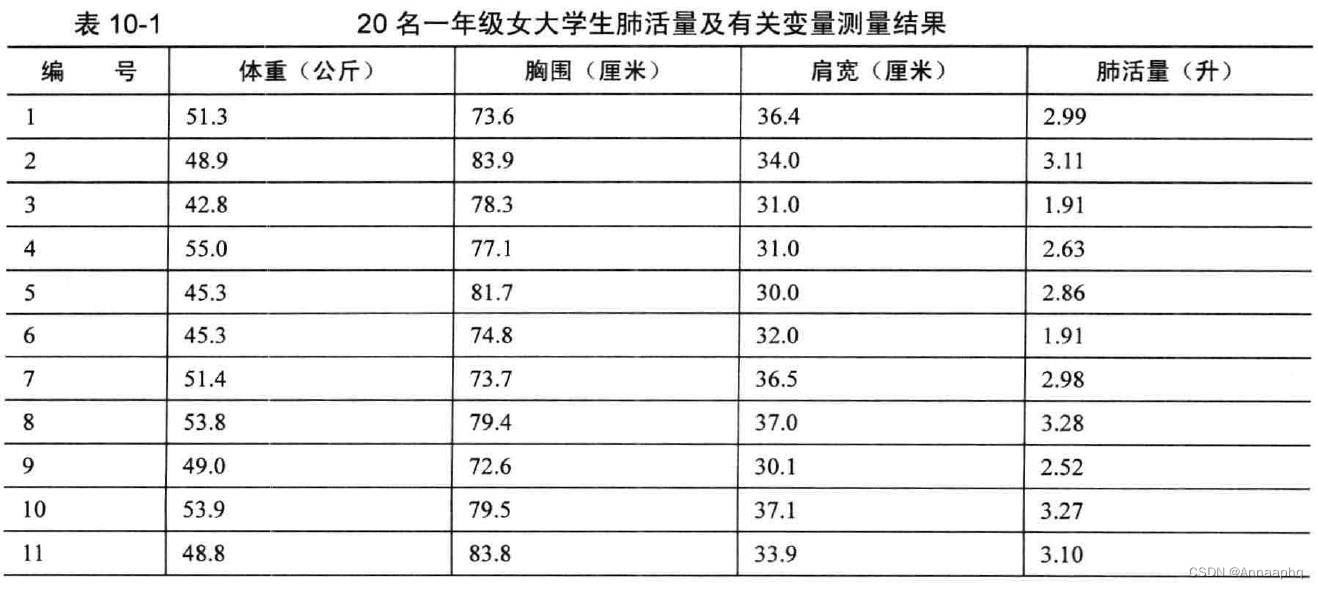
Example10_1 <- read.table ("example10_1.csv", header=TRUE, sep=",")
library(MASS)
attach(Example10_1)
fit1 <- lm(y~ x1 + x2 + x3)
fit2 <- lm(y ~ 1)
#可以采用统计学方向筛选出纳入回归方程的变量
stepAIC(fit2,direction="both",scope=list(upper=fit1,lower=fit2))
anova(fit1)
summary (fit1)
y #观察值
fitted (fit1) #预测值
residuals (fit1) #残差
detach (Example10_1)
备注:stepAIC方法中,如果去掉某一项后,AIC值降低,则该项应该被纳入回归方程中;也可以先用单变量线性回归,筛选出有价值的纳入回归方程
5、案例2
一家皮鞋零售店将其连续18 个月的库存占用资金情况、广告投入的费用、员工薪酬以及销售额等方面的数据作了一个汇总, 如表10-2 所示。该皮鞋店老板试图根据这些数据找到销售额与其他3 个变量之间的关系,以便进行销售额预测并为未来的预算工作提供参考。根据这些数据建立回归模型
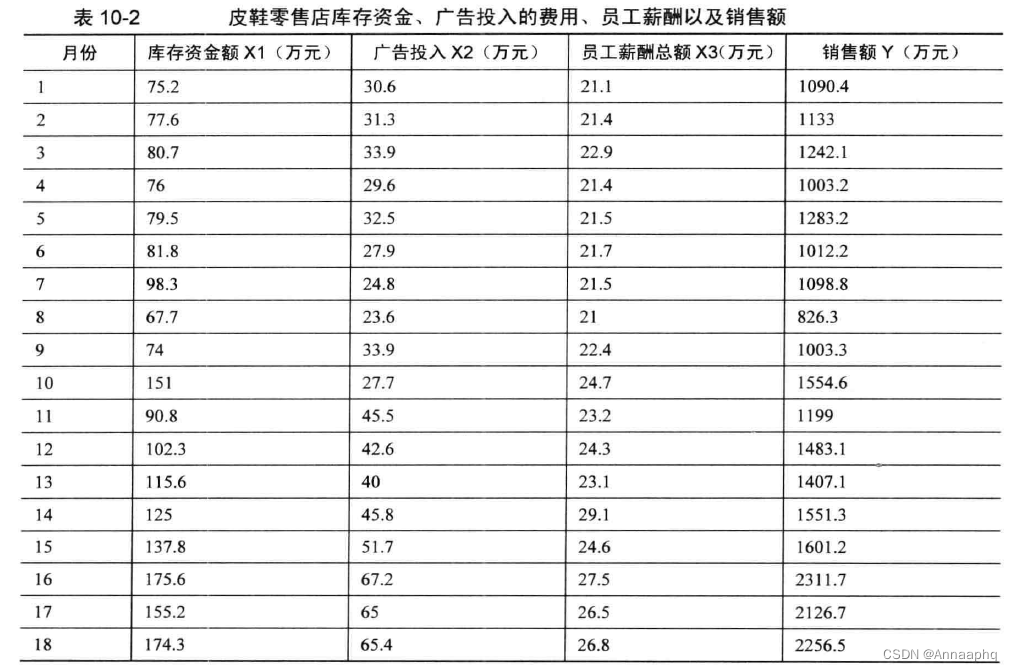
Example10_2 <- read.table ("example10_2.csv", header=TRUE, sep=",")
library(MASS)
attach(Example10_2)
fit1 <- lm(Y~ X1 + X2 + X3)
fit2 <- lm(Y ~ 1)
stepAIC(fit2,direction="both",scope=list(upper=fit1,lower=fit2))
fit <- lm(Y~ X1 + X2)
anova(fit)
summary (fit)
Y
fitted (fit)
residuals (fit)
detach (Example10_2)
四、用回归方法解决方差分析问题
线性回归分析与 t 检验等价
线性回归分析与方差分析等价
线性回归分析与协方差分析等价
回归分析适用于:因变量为计量资料,自变量为计量、分类或等级资料
ANOVA和回归都是广义线性模型的特例。因此,本章所有的设计都可以用 lm()函数来分析。但是,为了更好地理解输出结果,需要弄明白在拟合模型时, R是如何处理类别型变量的。以单因素ANOVA问题为例,即比较五种降低胆固醇药物疗法(trt)的影响:
library(multcomp)
levels(cholesterol$trt)
fit.aov <- aov(response ~ trt, data=cholesterol)
summary(fit.aov)
fit.lm <- lm(response ~ trt, data=cholesterol)
summary(fit.lm)
# fit.lm <- lm(response ~ trt, data=cholesterol, contrasts="contr.helmert") # wrong
fit.lm <- lm(response ~ trt, data=cholesterol, contrasts=list(trt="contr.helmert" ))
summary(fit.lm)
对照变量创建方法:

用线性回归解决协方差分析问题
以一个关于四膜虫细胞生长环境的数据集Tetrahymena 为例,该数据集出自Per Hellung-Larsen 。数据分别对应于两组不同的培养基,其中一组培养基中加入了葡萄糖,另外一组则没有。对于两组培养基, 分别记录其对应的平均细胞直径(μ) 和细胞密度(每毫升的细胞数量)。试验开始时设定了初始细胞浓度,两组的细胞密度之间不存在系统性差异。预期试验中的细胞直径会受到培养液中是否含葡萄糖的影响。
library(ISwR)
hellung
summary(hellung)
hellung$glucose <- factor(hellung$glucose, labels=c("Yes","No"))
summary(hellung)
attach(hellung)
plot(conc,diameter,pch=as.numeric(glucose))
legend(locator(n=1),legend=c("glucose","no glucose"),pch=1:2)#图形描述,按照圈和方形分别表示
plot(conc,diameter,pch=as.numeric(glucose),log="x")
plot(conc,diameter,pch=as.numeric(glucose),log="xy")
tethym.gluc <- hellung[glucose=="Yes",]#挑选出加入葡萄糖的
tethym.nogluc <- hellung[glucose=="No",]
lm.nogluc <- lm(log10(diameter)~ log10(conc),data=tethym.nogluc) #亚组分析
lm.gluc <- lm(log10(diameter)~ log10(conc),data=tethym.gluc) #亚组分析
abline(lm.nogluc)
abline(lm.gluc)
summary(lm(log10(diameter)~ log10(conc), data=tethym.gluc)) #亚组分析结果展示
summary(lm(log10(diameter)~ log10(conc), data=tethym.nogluc)) #亚组分析结果展示
var.test(lm.gluc,lm.nogluc) #比较两亚组回归模型
summary(lm(log10(diameter)~log10(conc)*glucose)) #考虑交互 全数据集
summary(lm(log10(diameter)~log10(conc)+glucose)) #未考虑交互,全数据集
anova(lm(log10(diameter)~log10(conc)*glucose)) #注意比较以下三种模型,自变量顺序很重要
anova(lm(log10(diameter)~glucose+log10(conc)))
anova(lm(log10(diameter)~log10(conc)+ glucose))
t.test(log10(diameter)~glucose)
anova(lm(log10(diameter)~glucose))
summary(lm(log10(diameter)~glucose))





















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








